算法练习--前缀和-优快云博客

1.前言

前缀和是一种在数组或序列中预先计算并存储部分和的技术。
通过构建一个前缀和数组，可以快速查询原始数组中任意区间的和。
前缀和时间复杂度为 $O (n)$ 的预处理，之后每次查询区间和的时间复杂度为 $O (1)$ 。

接下来我们来详细学习他

2.前缀和

(1) 以前的方法

首先我们思考一道题

给你一个整数数组，求整个数组所有元素的和

相信你一定会写

int sum=0;
for(int i=0;i<nums.length;i++){
	sum += nums[i];
}

但如果我们想求一个区间的和
也是一样

int sum=0;
for(int i=L;i<=R;i++){
	sum += nums[i];
}

但是如果有成千上万个元素,那么请问你怎么应对

while(Q--){
	int sum=0;
	for(int i=L;i<=R;i++){
		sum += nums[i];
	}
}

这个代码的时间复杂度已经是 $O (QN)$ 了
接下来我们正式学习前缀和

(2)一维前缀和

我们可以将结果存储到另一个数组

int[] preSum = new int[nums.length+1];
int sum=0;
for(int i=L;i<=R;i++){
	sum += nums[i];
	preSum[i] = sum;
}

这样另一个数组的元素就是从0到i的和

例:nums=[1,2,3,4,5,6,7,8,9,10]

比如在这个例子中
如果想求第三项到第八项的和
而此时preSum中的
第三项 = 3+2+1
第二项 = 2+1
第八项 = 8+7+6+5+4+3+2+1
我们发现这个和就等于第八项减去第二项

3+4+5+6+7+8 = 1+2+3+4+5+6+7+8-(1+2)

也就是 $s u m (m, n) = p [m] - p [n - 1]$

也就是说,我们只需要用 $O (n)$ 的时间处理前缀和,然后用 $O (1)$
的时间做一次减法就可以完成

其实这个代码还可以优化,并不需要有这个中间量sum
这个类似于阶乘
$5!=4!\times 5$
也就是
$p [i] = p [i - 1] + n u m s [i]$
当然,需要在0这里做一个特殊处理
我这里直接从1开始循环,也是一样的

public int[] preSum(int[] nums) {
	int[] preSum = new int[nums.length+1];
	for (int i = 1; i < =nums.length; ++i) {
		preSum[i] = preSum[i - 1] + nums[i-1];
	}
	return preSum;
}

(3) 二维前缀和

这个我们直接用题来讲解

Leetcode 304¹

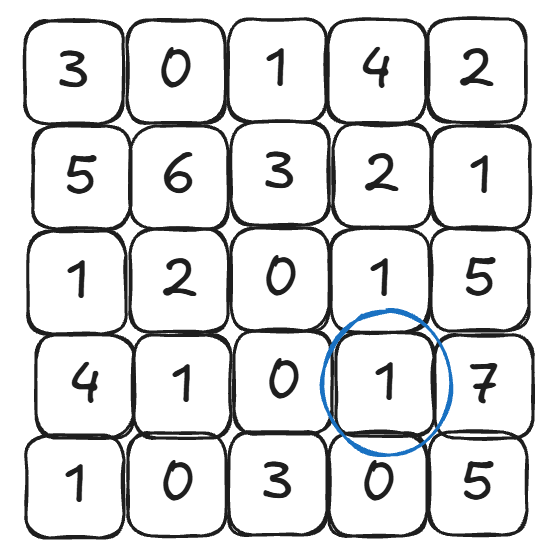
在这里插入图片描述
比如我们想要求这个圈出的1
这个1可以这样表示

再结合一个二维数组,就做出来了

class NumMatrix {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    public int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
}