WA变AC（NKOJ）

# 第一、将不顺眼的红色改为兴奋的绿色！

首先打开你的提交记录。

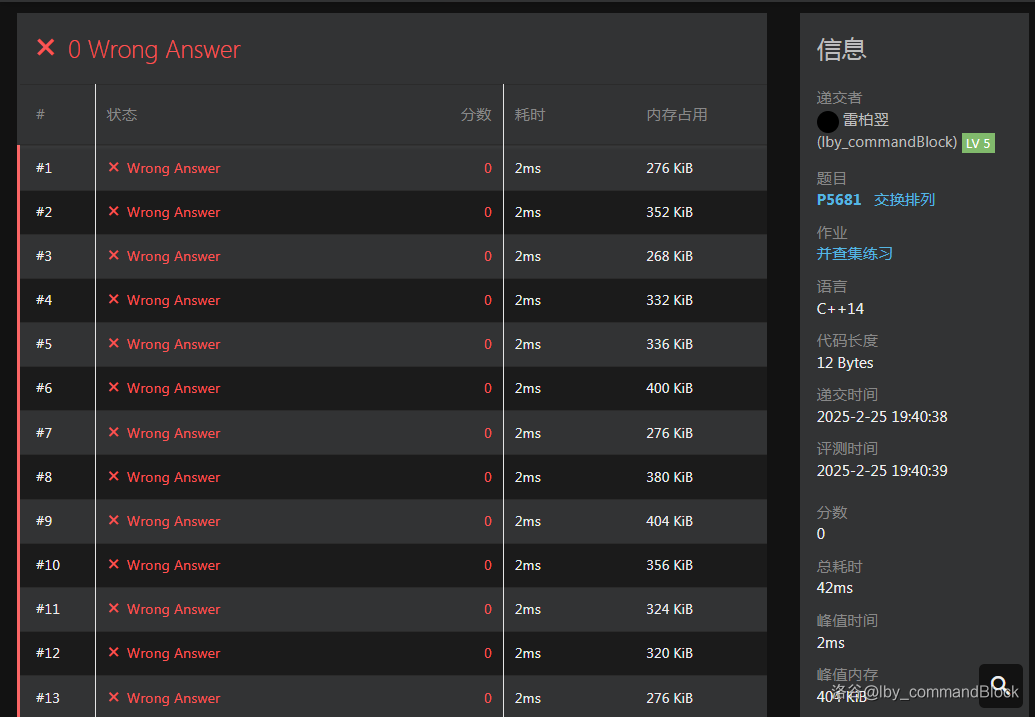
点击你的 F12，打开类似于这个的界面，随后点击“控制台”（或 Console）

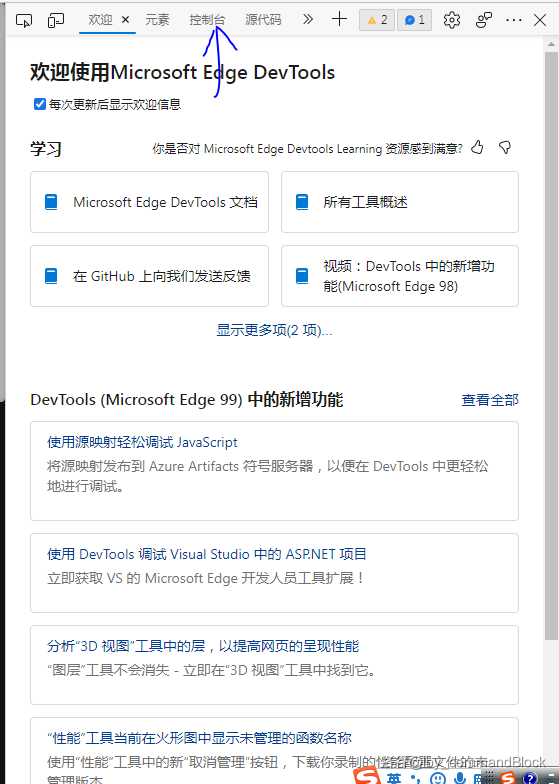
复制此代码，粘贴到控制台后点击回车确认，需要看到 `undefined` 字样表示成功：

var x = document.getElementsByClassName("fail");

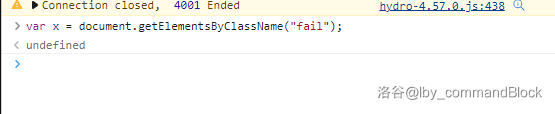
随后先输入这个指令：

for (var i = 0; i < x.length; i++)
 

此时应该有个缩进，如下图：

| 代表光标所在的位置。若正确，则继续输入以下代码：

x[i].classList.add("pass");