短语、直接短语、句柄、素短语、最左素短语的概念
短语:
在一个句型对应的语法树中, 以某非终结符为根的一棵子树的所有叶子自左至右排列起来形成一个相对于子树根的短语。
直接短语:
仅有父子两代的一棵子树,它的所有叶子自左至右排列起来所形成的符号串
句柄:
一个句型的分析树中最左那棵只有父子两代的子树的所有叶子的自左至右排列。
素短语:
素短语是这样的一个短语,它至少含一个终结符,并且,除它自身之外不再含任何更小的素短语。
最左素短语:
处于句型最左边的那个素短语。
依据语法树来求解
举例说明:
设文法G(E)为:
E -> E + T | T
T -> T * F | F
F -> (E) | i
(1)画出句型(T*F+i)的语法树。
(2)写出上述语句的短语,直接短语,句柄和素短语。
(1)
语法树:
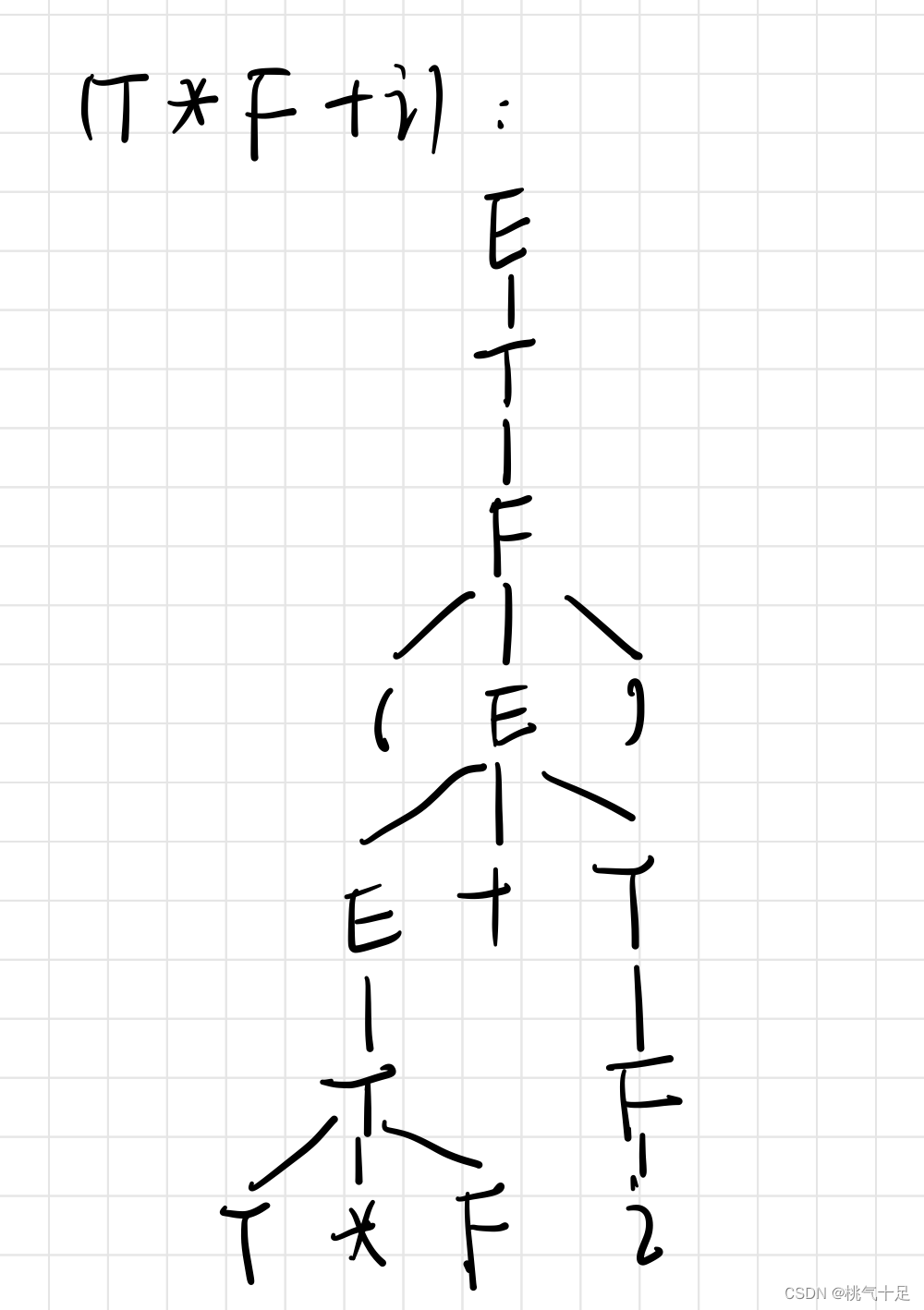
(2)
短语:T * F, i, T * F + i, (T * F + i)
直接短语:T * F, i
句柄:T * F
素短语:T * F, i
最左素短语:T * F








 文章介绍了短语、直接短语、句柄、素短语和最左素短语等概念,并通过文法G(E)和句型(T*F+i)的示例,展示了如何依据语法树来求解这些概念,其中(T*F)是句柄,最左素短语为T*F。
文章介绍了短语、直接短语、句柄、素短语和最左素短语等概念,并通过文法G(E)和句型(T*F+i)的示例,展示了如何依据语法树来求解这些概念,其中(T*F)是句柄,最左素短语为T*F。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










