离散数学实验----中国邮递员问题

原创

已于 2022-11-16 19:22:43 修改 · 6.4k 阅读

107 ·

CC 4.0 BY-SA版权

文章标签：

#图论 #算法

于 2022-11-16 19:21:58 首次发布

本文通过实验详细介绍了如何使用Dijkstra算法求解最短路径，Fleury算法求解欧拉回路，以及解决中国邮递员问题的完整流程。在给定的加权图G中，首先确定奇数度顶点，然后分组并添加最短路径，最后利用Fleury算法找到最优邮路。实验结果显示最短邮路长度为104单位，验证了算法的正确性。

实验目的和要求
1. 实验目的：

理解什么是欧拉图，熟悉欧拉路和欧拉回路的概念。
掌握Dijkstra算法，求解最短路径
掌握Fleury算法，求解欧拉回路。
了解Edmonds-Johnson算法解决中国邮递员问题的基本思路。
通过程序实现中国邮递员问题，强化其基本思想和实际应用。

1. 实验要求：
针对下图所示加权图G，给出中国邮递员问题的解决方案。
用流程图简述解决中国邮递员问题的流程。
对核心算法（如Dijkstra算法、Fleury算法）进行编程实现。
分析实验结果，验证其正确性。
总结实验，撰写实验心得。

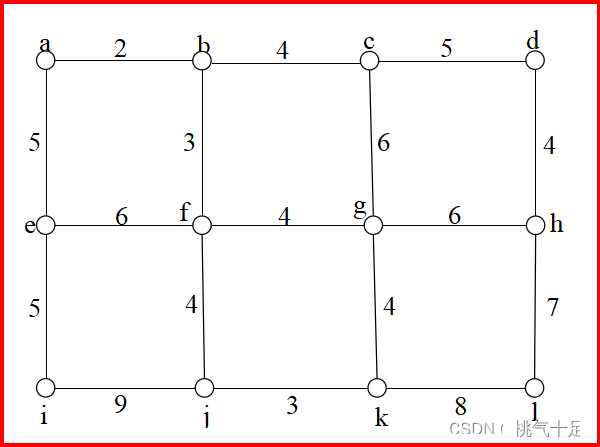
图G

实验环境和工具
1. 编程语言：

C++

1. 编程环境（编译器）：

Visual Studio 2019

实验结果
1. 算法流程图

解题思路：

求出图G中奇数度顶点集合
若奇数度顶点个数为0<=>图G为欧拉图，直接使用Fleury算法求出欧拉回路，即最优邮路。
若奇数度顶点个数为2n（n=1，2，3......）<=>图G不是欧拉图，需添加一些重边。
用Dijkstra算法求出奇数度顶点两两之间的最短距离。
将奇数度顶点两两分组，遍历所有组合情况，根据已经求出的最短距离，找出最短的组合方式，即最优分组。
根据最优分组情况为图G添加重复边。
对添加重复边之后得到的图G’利用Fleury算法，求出欧拉回路，即此时的最优邮路。

流程图：

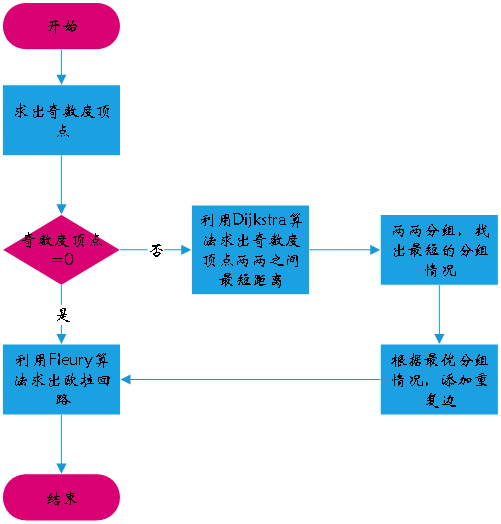
整体算法流程图

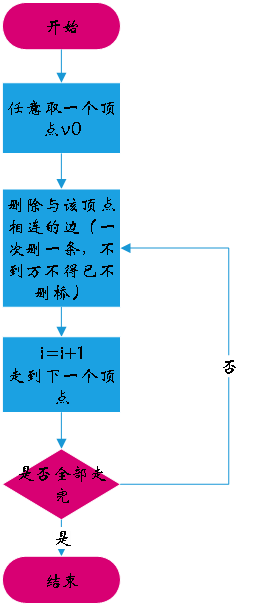
Fleury算法流程图

程序核心代码


判断是否为连通图：

bool ConnectivityTest(int start, bool& bNoPoints){

set<int> nodeSet; // 连通顶点集

vector<int> test_nodes; // 与新加入连通点连通的未加入点集

set<int> singlePoints; // 图中的单点集

int i, j;

// 先找出单点

bool hasEdge = false;

for (i = 0; i < V; i++){

hasEdge = false;

// 这里起始应该是0，不然最后一个点如果是单点则无法判断

for (j = 0; j < V; j++) {

if (Graph[i][j] > 0){

hasEdge = true;

break;

}

}

if (!hasEdge){

singlePoints.insert(i);

}

}

// 设置bNoPoints标志

bNoPoints = (singlePoints.size() == V);

// start点必须在连通图中

if (singlePoints.find(start) != singlePoints.end()) {

return false;

}

test_nodes.push_back(start);



while (test_nodes.size() > 0){

int testNode = test_nodes.back();

test_nodes.pop_back();

for (i = 0; i < V; i++){

if (Graph[testNode][i] > 0){

i