LR与svm 简单应用
- 算法定义
- 基本实践
算法定义
LR算法
逻辑回归
logistic回归是一个分类算法,是一种广义的线性回归分析模型,它常用处理处理二元分类以及多元分类问题
逻辑回归问题的起点:
线性回归模型是表征了输出向量Y和输入样本矩阵x之间的线性关系,其线性关系的参数为θ,此时模型的预测是的值域为(-∞,+∞),并且我假设y 是连续的。如果最终我们需要y 的结果是一个有限集的,比如是一个简单的分类问题,那么我们需要一个函数转换,使得y 值可以映射在一个有限的区间上。 比如以二分类问题为例:
推理过程
我们引入转换函数sigmoid,如下图所示:

将函数的输入范围(∞,-∞)映射到了输出的(0,1)之间且具有概率意义.具有概率意义是怎么理解呢:将一个样本输入到我们学习到的函数中,输出0.7,意思就是这个样本有70%的概率是正例,1-70%就是30%的概率为负例.。
则真个函数就变换为:
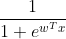
接下来就是如何构造损失函数的问题:
- 从似然函数的角度去构建
- 类似感知机模型,从损失判断去度量,如下:
如下图所示:如果y=1时, 即p>0.5, 这个时候概率p越小, 被错分为y=0的几率越大,损失函数便会越大。与之对应,如果y=0时, 即p<0.5, 这个时候概率p越大, 被错分为y=1的几率越大,损失函数便会越大。因此我们想到了下面的log函数。

则整个解析式loss 函数可写为:

最终的loss 函数为:

然后求导,得优化解:

SVM 算法
问题引入
如下,在线性分类中,平面上有两类数据,我们可以找到多条直线将两类数据分开,但是,那个才是最好的呢?

我们可以看出,假设存在一条直线是最优划分,则必然满足:
1、能够正确划分训练数据集
2、并且几何间隔最大的分离超平面
其数学公式表示为:
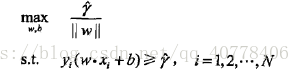
可化简为:

对上述函数的求解可转化为,拉格朗日条件极值问题,构建函数如下:
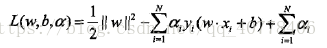
根据原问题的对偶性和约束条件我们可解得:
具体过程,手动求解
代码实践
tfdif=TfidfVectorizer()
train_data_feature=tfdif.fit_transform(train_data['word_seg'])
print(train_data_feature)
x_train,x_validation,y_train,y_validation=train_test_split(train_data_feature,y,test_size=0.3,random_state=2019)
print(x_train.shape)
print(x_validation.shape)
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.metrics import accuracy_score,precision_score,f1_score
logis=LogisticRegression(C=1,dual=True)
logis.fit(x_train,y_train)
y_pre=logis.predict(x_validation)
f1=f1_score(y_validation,y_pre,average='micro')
print("the f1 score: %.2f"%f1)
svm=LinearSVC(C=1,dual=True)
svm.fit(x_train,y_train)
y_pre=svm.predict(x_validation)
f1=f1_score(y_validation,y_pre,average='micro')
print("the f1 score: %.2f"%f1)
最终结果:
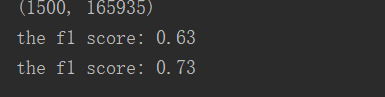
参考:
[1] https://blog.youkuaiyun.com/zhangyunpeng0922/article/details/85125438
[2] https://blog.youkuaiyun.com/weixin_39445556/article/details/83930186
[3] https://blog.youkuaiyun.com/u012033832/article/details/78519422
[4] https://blog.youkuaiyun.com/qq_40778406/article/details/79879434c
[5] https://blog.youkuaiyun.com/qq_32241189/article/details/79881782
[6] https://blog.youkuaiyun.com/d__760/article/details/80387432




















 2743
2743

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








