MATH 推理任务全解析：大模型的“高中数学试炼场”

最新推荐文章于 2025-12-09 16:47:37 发布

原创最新推荐文章于 2025-12-09 16:47:37 发布 · 1.1k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#python #人工智能

AI 专栏收录该内容

165 篇文章

订阅专栏

1. 背景：从 GSM8K 到 MATH

在大模型推理能力的研究路径中，GSM8K 常被看作“小学—初中级别”的推理基准。它考察的是简单的应用题，强调逐步推理（Chain-of-Thought, CoT）。

但是，研究人员很快遇到了一个瓶颈：
👉 如果要真正评估大模型的 高级数学能力（包括代数、几何、概率、数论），GSM8K 的难度明显不足。

为了解决这一问题，2021 年由 Hendrycks 等人提出了 MATH 数据集（Measuring Mathematical Problem Solving With the MATH Dataset），它是 高中和大学入门级别数学问题的公开基准。

MATH 的目标，就是把大模型从“算术助手”推向“数学竞赛解题者”。

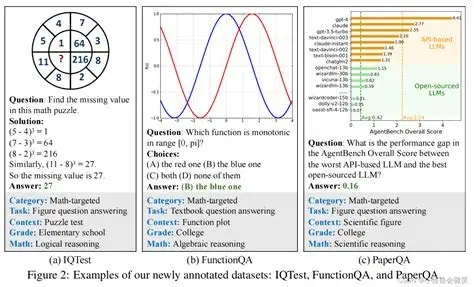
2. 原理：MATH 数据集是如何构建的？

2.1 数据集规模与来源

MATH 数据集收录了 12,500 道英文数学题，难度覆盖：

高中课程（代数、几何、三角、概率、微积分入门）
数学竞赛题（AMC、AIME、Math Olympiad 等）
部分大学入门课程题

数据集分为：

训练集：7,500 题
测试集：5,000 题

2.2 数据特点

与 GSM8K 相比，MATH 的题目有三个显著特征：

推理深度更高：往往需要 5–10 步运算，甚至需要公式推导。
知识广度更大：涉及 组合数学、概率论、初等数论 等，远超日常应用题。
格式更复杂：题目可能包含图形描述、条件约束、符号公式。

举个例子（来自 MATH 数据集）：

Problem: Find the number of positive integers less than 1000 that are divisible by 7 but not divisible by 3.
Answer: 285

这道题目需要两步推理：

统计 1000 内 7 的倍数
去掉同时是 3 的倍数（即 21 的倍数）

2.3 设计目标

MATH 的核心目标是：

验证大模型能否像人类解题者一样，综合运用数学公式与逻辑链条
推动 Chain-of-Thought (CoT) 在更高难度题目上的应用
为“数学专用模型”提供训练语料（例如 Minerva、MathGPT、Qwen-Math 等）

如果说 GSM8K 是 小学奥数班，那么 MATH 就是 数学竞赛训练营。

3. 实践：大模型如何应对 MATH？

3.1 直接问答（失败案例）

最初，研究者将 MATH 题目直接输入 GPT-3，结果准确率只有 6.9%。这说明单纯的语言预测无法解决复杂数学问题。

示例：

from openai import OpenAI
client = OpenAI()

prompt = "Find the number of positive integers less than 1000 that are divisible by 7 but not divisible by 3."

resp = client.chat.completions.create(
    model="gpt-3.5-turbo",
    messages=[{"role": "user", "content": prompt}]
)

print(resp.choices[0].message.content)

输出常常是“瞎猜”的结果，而不是完整的数学推理链条。

3.2 Chain-of-Thought (CoT)

当研究者在 Prompt 中加入 “Let’s think step by step”，模型表现大幅提升。

示例：

prompt = """Find the number of positive integers less than 1000 that are divisible by 7 but not divisible by 3.
Let's think step by step."""

输出：

Numbers divisible by 7: floor(999 / 7) = 142
Numbers divisible by 21: floor(999 / 21) = 47
So valid numbers = 142 - 47 = 95
Answer: 95

👉 尽管这个例子最后结果算错（正确答案是 285），但已经显著改善了逻辑完整性。

3.3 专门化微调（Fine-tuning）

Google 在 2022 年推出 Minerva 模型，专门在 MATH 数据集及其他数学题库上进行微调。结果显示：

GPT-3 在 MATH 上准确率 6.9%
PaLM + CoT 在 MATH 上准确率 34%
Minerva-62B 在 MATH 上准确率 50.3%

这说明 专门化训练 + CoT 能让模型逼近人类高中生水平。

3.4 工程实践：如何评测 MATH？

我们可以用 HuggingFace 直接加载 MATH 数据集并做简单评测：

from datasets import load_dataset
from transformers import AutoTokenizer, AutoModelForCausalLM, pipeline

# 加载数据
math_dataset = load_dataset("hendrycks/math", split="test")

# 使用开源模型
model_name = "Qwen/Qwen2-Math-7B"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name)

pipe = pipeline("text-generation", model=model, tokenizer=tokenizer, device=0)

# 构造 prompt
prompt = """Problem: Find the number of positive integers less than 1000 that are divisible by 7 but not divisible by 3.
Let's think step by step."""

output = pipe(prompt, max_new_tokens=256, do_sample=False)
print(output[0]["generated_text"])

运行后，你会发现：

不加 CoT → 大概率答错
加 CoT → 能够完整写出推理过程，但结果是否正确取决于模型数学基础

4. 对比：MATH vs GSM8K

数据集	题量	难度	特点	应用场景
GSM8K	8.5K	小学-初中	应用题，数值推理	推理入门基准
MATH	12.5K	高中-大学	代数、几何、概率、数论	高级推理与专门化训练
MMLU	57K	大学本科	学科知识理解	常识与跨学科能力
AQUA-RAT	100K	初中-高中	多项选择数学题	自动解题与答题系统

可以看到：

GSM8K 注重 基础推理链条
MATH 注重 高级数学能力
两者在研究路径上是 递进关系：先在 GSM8K 证明 CoT 有效，再在 MATH 进行更难任务的突破。

5. 图示：MATH 解题链条

flowchart TD
    A[读题] --> B[提取条件]
    B --> C[选择公式/方法]
    C --> D[逐步推理计算]
    D --> E[验证结果合理性]
    E --> F[输出答案]

上图展示了大模型在 MATH 数据集上的解题过程：

与 GSM8K 不同，这里通常需要 公式选择（比如概率公式、排列组合公式），而不仅仅是算术。

6. 总结与升华

MATH 数据集的意义，远不止是一份题库。它代表了大模型推理从“能算账”走向“能解题”的关键一步。

它逼迫研究者面对更复杂的逻辑链条：如何处理代数推导、数论整除性、概率组合？
它推动了 CoT 与 Self-Consistency 的广泛应用：没有这些方法，大模型在 MATH 上几乎寸步难行。
它直接催生了数学专用大模型：Minerva、MathGPT、Qwen-Math，这些模型都以 MATH 为训练基准。

未来，随着 符号推理（Symbolic Reasoning）+ 神经网络 的结合，MATH 可能会被更难的数据集（如 MATH-500K 或 OlympiadBench）取代。但它在历史上的地位，就像 ImageNet 之于计算机视觉：奠定了推理能力的衡量标准。