Pytorch框架学习（9）——权值初始化

最新推荐文章于 2024-11-13 11:23:05 发布
原创 最新推荐文章于 2024-11-13 11:23:05 发布 · 310 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python #pytorch

本文探讨了梯度消失与梯度爆炸的问题，介绍了Xavier与Kaiming两种权重初始化方法，旨在帮助深度学习模型更好地收敛。文章详细解释了两种方法背后的理论依据，并对比了它们适用的不同激活函数。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

1. 梯度消失与梯度爆炸

不恰当的权值初始化可能会引起梯度消失或者梯度爆炸。
我们从一个例子中来理解梯度消失与梯度爆炸。，下图给出一个两层网络，我们来计算一下 W 2 W_2 W2​的梯度。
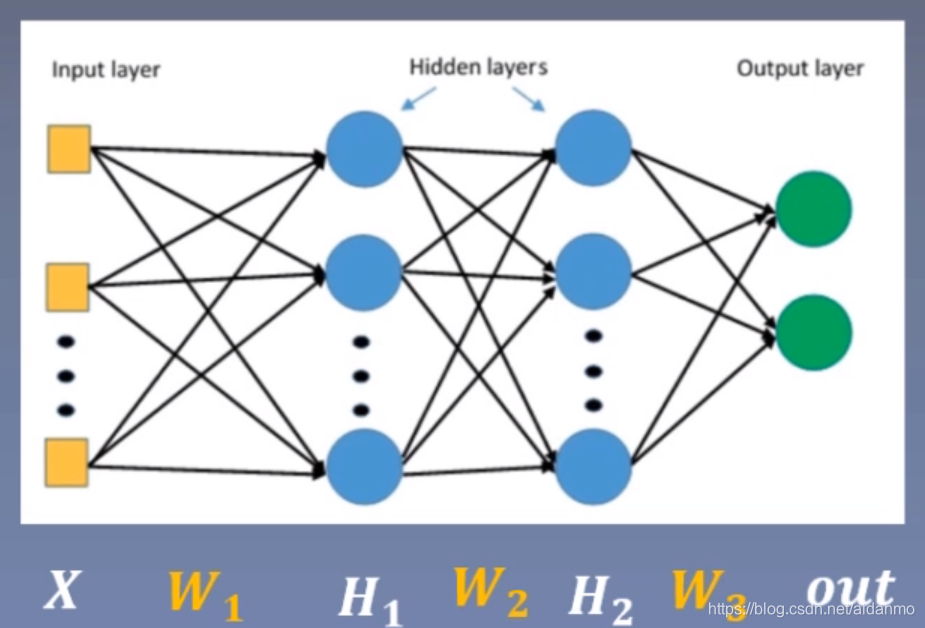
在这里插入图片描述
在这里插入图片描述
从计算过程中可以看到，当 H 1 H_1 H1​趋近于0时，会导致 W 2 W_2 W2​的梯度趋近于0，造成梯度消失；当 H 1 H_1 H1​趋近于无穷时，会导致 W 2 W_2 W2​的梯度趋近于无穷，造成梯度爆炸。
因此，要避免梯度消失或者梯度爆炸，就要控制网络输出层的值的尺度范围，也就是每一层网络输出值不能过大或者太小。

2. Xavier方法与Kaiming方法

2.1 Xavier初始化

  • 方差一致性：保持数据尺度维持在恰当范围，通常方差为1（尽量让每个网络层输出的方差等于1）
  • 激活函数：饱和函数，如Sigmoid， Tanh
    在这里插入图片描述
    n i n_i ni​是输入层的神经元个数， n i + 1 n_{i+1} ni+1​表示输出层神经元的个数，权值w的初始化值可按照上述公式推导方法得到。

2.2 Kaiming初始化

参考文献《Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification》

  • 方差一致性：保持数据尺度维持在恰当范围，通常方差为1
  • 激活函数：ReLU及其变种

3. 常用初始化方法

  1. Xavier均匀分布
  2. Xavier标准正态分布
  3. Kaiming均匀分布
  4. Kaiming标准正态分布
  5. 均匀分布
  6. 正态分布
  7. 常数分布
  8. 正交矩阵初始化
  9. 单位矩阵初始化
  10. 稀疏矩阵初始化
  • nn.init.calculate_gain
    • 功能：计算方法变化尺度：输入数据的方差除以经过激活函数之后输出数据的方差。
    • 主要参数
      • nonlinearity：激活函数名称
      • param：激活函数的参数，如leaky ReLU的negative_slop
pytorch权重初始化
安静到无声
06-25 3230
我们定义的网络如下所示 VGG( (features): Sequential( (conv0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (norm0): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) (relu0): ReLU(inplace=True) (conv1
从零实现深度学习框架——几种常用的权重初始化方法
日积月累，天道酬勤
04-21 2642
近两万字详细解释Xavier初始化和He初始化的由来，并有详尽的推理证明！
Pytorch 实现权重初始化
09-18
今天小编就为大家分享一篇Pytorch 实现权重初始化，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧
vgg16网络初始化权重
12-14
从谷歌上找了好久的，而且网速还贼拉的慢，为方便大家，上传共享
CS231n笔记7-ConvNets Typical Architecture与VGGNet
u012767526的专栏
05-18 1万+
ConvNets Typical Architecture与VGGNetConvNets Typical Architecture-卷积神经网络经典结构写到这里，小编已经大体覆盖了构建一个大型卷积神经网络所需要的知识点。下面是小编在上课是总结的卷积神经网络的结构。 读者是不是觉得上面的图的那些英文都似曾相识，是的，小编在之前的学习笔记中都有介绍，为了方便读者阅读，下面小编给出相应的链接 Con
神经网络中权重的初始化
qq_14926777的博客
07-16 359
参考文献：http://cs231n.github.io/neural-networks-2/#inithttps://blog.youkuaiyun.com/marsggbo/article/details/77771497
PyTorch框架学习十一——网络层权值初始化
qq_40467656的博客
08-18 700
PyTorch框架学习十一——网络层权值初始化一、均匀分布初始化二、正态分布初始化三、常数初始化四、Xavier 均匀分布初始化五、Xavier正态分布六、 前面的笔记介绍了网络模型的搭建，这次将介绍网络层权值的初始化，适当的初始化方法可以使得避免梯度消失或梯度爆炸等问题，还能一定程度上加快网络的训练迭代过程。 下面将介绍PyTorch中十种常用的权值初始化的方法： 一、均匀分布初始化 torch.nn.init.uniform_(tensor: torch.Tensor, a: float = 0.0,
深度学习day1|用pytorch框架实现手写数字识别
最新发布
weixin_53754431的博客
11-13 1524
本文介绍了如何使用PyTorch进行手写数字识别，构建了LeNet-5模型并进行训练，展示了训练过程和结果可视化。
pytorch学习之路——01
weixin_35338624的博客
10-18 772
本节主要学习transforms、pytorch框架下建立全连接网络、查看每一层参数以及前向传播 import torch from torch import nn import torch.nn.functional as F import matplotlib.pyplot as plt from torchvision import datasets,transforms trans...
09—《动手学深度学习——Pytorch版》—权重衰退
qq_46670313的博客
04-19 1303
在训练参数化机器学习模型时， 权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2L2L2正则化。L2L2L2下面的代码将模型拟合训练数据集，并在测试数据集上进行评估。线性网络和平方损失没有变化， 所以我们通过d2l.linreg和d2l.squared_loss导入它们。唯一的变化是损失现在包括了惩罚项。def train(lambd): # 训练模型，lambd为权重衰减系数w, b = init_params() # 初始化模型参数我w,b。
为了更够更好地学习基于框架pytorch的深度学习，特地创建该仓库
05-10
深度学习（DL，Deep Learning）是机器学习（ML，Machine Learning）领域中一个新的研究方向，它被引入机器学习使其更接近于最初的目标——人工智能（AI，Artificial Intelligence）。 [1] 深度学习是学习样本数据的...
权重初始化方法及适用情况
Loong Cheng的博客
06-19 5928
1. Gaussian 从具有固定均值（例如0）和固定2的标准差（例如0。01）的搞死分布中随机抽取权重，这是最常用的. 一般使用截断高斯。 2. Xavier 这种方法是但的缩放均值或者搞死分布进行初始化 在caffe,他通过从零均值和特定方差的分布中绘制他们来初始化网络中的权重。 其中w是所有讨论的神经元的初始化分布，而n_in是摄入神经元的神经元的数量，使用的分布通常是高斯...
pytorch加载自定义网络权重
热门推荐
qq_34789262的博客
10-25 1万+
在将自定义的网络权重加载到网络中时，报错： AttributeError: 'dict' object has no attribute 'seek'. You can only torch.load from a file that is seekable. Please pre-load the data into a buffer like io.BytesIO and try to lo...
pytorch—权重初始化
scorpioto的博客
03-02 544
torch.nn.init (一）随机 torch.nn.init.uniform(tensor, a=0, b=1) 从均匀分布U(a, b)中生成值 torch.nn.init.normal(tensor, mean=0, std=1) 从给定均值和标准差的正态分布N(mean, std)中生成值 （二）常数 torch.nn.init.constant(tensor, val) 用val填充 （三） torch.nn.init.kaiming_normal(tensor, a=0, mode='
[pytorch]权重初始化方法
weixin_43844219的博客
03-29 3639
[pytorch]权重初始化方法 权重初始化的方法封装在torch.nn.init里。具体在使用的时候先初始化层之后直接调，e.g. conv = nn.Conv2d(*args, **kwargs) conv.weight.data.normal_() #w以标准正态分布初始化 conv.bias.data.zero_() #偏置以0初始化 常数初始化 w = torch.empty(3,...
Pytorch框架学习（6）——transforms与normalize
aidanmo的博客
01-28 1万+
图像预处理Transforms与normalize 文章目录图像预处理Transforms与normalize1. transforms运行机制2. 数据标准化——transforms.normalize 1. transforms运行机制 torchvision工具包中包含三个主要模块，今天主要学习transforms torchvision.transforms:常用的数据预处理方法，提升...
pytorch第四次作业-DataLoder与数据预处理
aidanmo的博客
01-21 1003
1. 采用步进(Step into)的调试方法从 for i, data in enumerate(train_loader) 这一行代码开始，进入到每一个被调用函数，直到进入RMBDataset类中的__getitem__函数，记录从 for循环到RMBDataset的__getitem__所设计的类与函数？ 第一步：for i, data in enumerate(train_loader...
Pytorch框架学习（5）——DataLoder与Dataset
aidanmo的博客
01-21 681
Dataloder与DataSet 文章目录Dataloder与DataSet1. 人民币二分类2. DataLoder与Dataset2.1 DataLoder2.2 DataSet2.3 数据读取 1. 人民币二分类 今天主要分享机器学习训练过程的数据处理过程。 数据： 数据收集：Img，Label 数据划分：训练集，验证集，测试集 数据读取：DataLoder（Sampler：生成索引...
Pytorch框架学习（16）—— Normalization
aidanmo的博客
02-27 651
文章目录1. Why Normalization2. Batch Normalization3. Layer Normalization4. Instance Normalization5. Group Normalization 1. Why Normalization 因为在深度学习当中存在ICS（Internal Covariate shift）问题：数据尺度/分布异常，导致训练困难 从公...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Aidanmomo

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值