知识图谱学习笔记（五）——实体识别（2）

实体识别（信息抽取）

知识图谱学习笔记（五）——实体识别(1)

2. 信息抽取的基础：分词和词性标注

2.6基于统计的分词方法

基于统计的方法需要标注训练语料训练模型，可分为生成式统计分词和判别式统计分词

2.6.1 生成式方法

• 生成式方法优缺点
  • 优点：在训练语料规模足够大和覆盖领域足够多的情况下，可以获得较高的切分正确率
  • 缺点：训练语料的规模和覆盖领域不好把握。模型实现复杂、计算量较大。

2.6.2 判别式方法

• 原理：在有限样本条件下建立对于预测结果的判别函数，直接对预测结果进行判别。由字构词的分词理念，将分词问题转化为判别式分类问题。

• 典型算法：Maxent SVM CRF Perceptron

• 分词流程：

  • 把分词问题转化为确定居中每个字在词中位置问题
  • 每个字在词中可能的位置可以分为以下四种：词首（B），词中（M），词尾（E），独字（S）。

• 分词结果展示

  • 分词结果：毛/B新/M年/E2/B0/M0/M0/M年/E毕/B业/E于/S东/B北/M大/M学/E

• 最大熵模型

• 最大熵理论：

  • 在无外力作用下，事物总是朝着最混乱的方向发展
  • 事物是约束和自由的统一体
  • 事物总是在约束下争取最大的自由权，这其实也是自然界的根本原则
  • 在已知条件下，熵最大的事物，最可能接近它的真实状态

• 基于最大熵原理的模型选择

  • 任务：研究某个随机事件，根据已知信息，预测其未来行为。
  • 方法：当无法获得随机事件的真实分布时，构造统计模型对随机事件进行模拟。
  • 难点：满足已知信息要求的模型可能有很多个，用哪个模型来预测最合适呢？
    1. 原则熵最大的模型
    2. Jaynes证明：对随机事件的所有相容的预测中，熵最大的预测出现的概率占绝对优势
    3. Tribus证明：正态分布、伽玛分布、指数分布等，都是最大熵原理的特殊情况。
       

• 最大熵模型：天气预报
  假设要用今天的天气预测明天的天气。

  • 天气$\in${晴、阴、雨}
  • 风向$\in${无、南、北}
  • 已知今天的天气和风向，要预测明天的天气

• 样本数据如下所示：
  

• 问题定义：
  

• 建模

  • 建立天气预报模型：给出所有可能的条件下结论的概率$P(\beta |\alpha )，\alpha \in A，\beta \in B$
  • 为简化问题，通常用联合概率模型取代上述的条件概率模型$P(\alpha ，\beta )$
  • 二者关系：$P(\beta |\alpha )=P(\alpha ,\beta )/P(\alpha )$
  • 由于条件和结论都是离散量，理论上，所有的可能性是可以穷举的，因此只要给出所有可能性的概率即可。
    

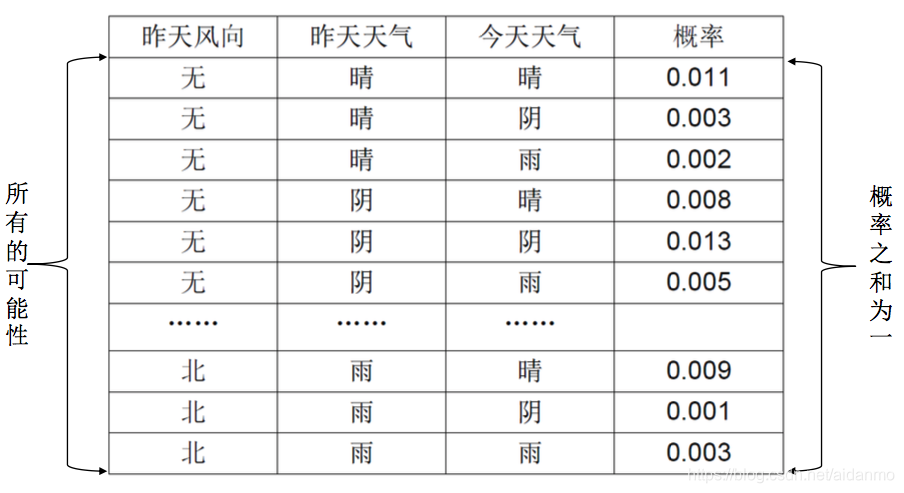
• 上述模型需要满足以下两个条件：

  • 模型的概率分布应尽可能与样本一致
    
  • 模型的熵最大

• 优化目标：

  • X熵最大：可以表示为：