（BBED）减少基于扩散的语音增强的随机微分方程的先验不匹配

Reducing the Prior Mismatch of Stochastic Differential Equations for  Diffusion-based Speech Enhancement

摘要

最近，得分生成模型已成功应用于语音增强任务中。随机微分方程用于建模迭代的正向过程，在每个步骤中将环境噪声和白噪声添加到清晰的语音信号中。虽然在极限情况下，正向过程的均值最终停止于嘈杂的混合物，但在实践中，它会提前停止，因此只能近似到嘈杂的混合物。这导致了正向过程的终止分布和推理时用于解决反向过程的先验之间存在差异。本文解决了这个差异。为此，我们提出了一个基于布朗桥的正向过程，并展示这种过程相比以前的扩散过程可以减少不匹配。更重要的是，我们证明了我们的方法在客观指标上优于基线过程，而且只需要一半的迭代步骤并且有一个更少的超参数需要调整。

关键词：语音增强，扩散模型，随机微分方程，布朗桥。

1 介绍

语音增强的目标是从受环境噪声污染的嘈杂混合物中恢复清晰的语音信号。传统方法尝试利用清晰语音信号和环境噪声之间的统计关系。已经提出了许多机器学习方法，将语音增强视为一项判别性学习任务。

与直接学习从嘈杂语音到干净语音的判别式方法不同，生成式方法学习干净语音数据的先验分布。最近，所谓的基于得分的生成模型（或扩散模型）被引入到语音增强的任务中[5-9]。其思想是使用称为正向过程的离散且固定的马尔可夫链迭代地向数据添加高斯噪声，从而将数据转换为可处理的分布，例如正态分布。然后，训练神经网络来反转这个扩散过程，在所谓的反向过程中[10]。当两个离散马尔可夫链状态之间的步长趋近于零时，离散马尔可夫链在温和约束下变成了连续时间随机微分方程（SDE）。利用SDE比基于离散马尔可夫链的方法提供了更大的灵活性和机会[11]。例如，SDE允许使用通用SDE求解器对反向过程进行数值积分，影响性能和迭代步数。SDE可以解释为两个给定分布之间的变换，其中一个被称为初始分布，另一个被称为终止分布。在语音增强的情况下，我们在干净语音数据的分布和嘈杂混合数据的分布之间进行转换。在温和约束下，我们可以为每个正向SDE找到一个反向SDE来反转正向SDE[12,13]。这个反向SDE从嘈杂的混合开始，最终得到干净的语音。因此，它可以用于语音增强。

目前，针对语音增强的任务，有不同的方法将环境噪声的污染集成到扩散过程中[6-8]。为了补偿非高斯噪声特征，这些方法沿着正向过程使用干净语音和嘈杂语音数据之间的插值。在[7,8]中使用了连续时间SDE，其中包括一个漂移项，允许干净语音和嘈杂语音之间的转换。有趣的是，在[7,8]中的过程的均值仅在一个无限长的正向扩散过程中从干净语音完美地演变为嘈杂语音。然而，在实践中，正向过程的均值以嘈杂语音数据的近似值结束。因此，在解决反向SDE以进行语音增强时，正向过程的终止分布和反向过程的初始分布存在不匹配[8]。我们将反向过程的初始分布称为生成模型的先验分布，相应的不匹配称为先验不匹配。此外，[7,8]中的SDE包括一个刚度参数，控制清晰语音数据对噪声语音数据的拉力。因此，这个刚度参数决定了所得到的先验不匹配程度。增加刚度可以减少先验不匹配，但也可能对语音增强性能产生负面影响，因为反向过程可能变得不稳定[8]。

为了克服这个限制，我们寻求在不破坏反向过程的情况下减少先验不匹配。为此，我们提出用基于布朗桥过程的SDE替换[7,8]中的正向过程。布朗桥似乎适用于此目的，因为它具有固定的起点和终点，并在中间遵循布朗运动。我们展示了所得到的扩散过程不仅极大地减少了先验不匹配，而且消除了[7,8]中SDE的依赖于数据集且难以调节的刚度参数。在实验中，我们证明了使用所提出的SDE比基线SDE更有效，同时只需调节一个超参数并使用一半的函数评估次数。

2 背景

2.1 随机微分方程 

3 不同SDE的设计选择

3.1 具有方差爆炸的（Ornstein-Uhlenbeck）OU过程（OUVE）

 

 3.2 指数扩散系数布朗桥（BBED）

4 实验设置

为了公平比较 BBED SDE 和 OUVESDE，我们使用相同的配置训练相应的评分模型，并按照 [8] 中的实验设置进行实验。

4.1 训练

对于评分模型 sθ(Xt, Y, t)，我们采用 Noise Conditional Score Network (NCSN++) 架构（更多细节见 [8, 11]）。网络基于去噪评分匹配进行优化： argminθEt,(X0,Y),Z,Xt|(X0,y) "sθ(Xt, Y, t) +Zσ(t)22# ，(14) 其中 Xt = µ(t) + σ(t)Z，Z∼ NC(0, I)。我们使用学习率为 10−4 和批大小为 16 进行网络训练。使用 0.999 的衰减率跟踪网络参数的指数移动平均值，用于采样 [7, 11]。我们训练 250 个 epoch，并在训练期间记录来自验证集的 10 个随机文件的平均 PESQ 值，并选择表现最好的模型进行评估。实验在 NVIDIA A6000 上进行，训练大约需要 4 天的时间。

4.2 数据集和输入表示

我们使用与 [8] 中相同的 WSJ0-CHiME3 数据集。该数据集将来自 Wall Street Journal (WSJ0) 数据集 [17] 的干净语音话语与 CHiME3 数据集 [18] 中的噪声信号混合，并使用均匀采样的信噪比（SNR）在 0 到 20 dB 之间。该数据集被分成训练集（12777 个文件）、验证集（1206 个文件）和测试集（615 个文件）。WSJ0-CHiME3 数据集中的每个文件都被转换为具有 510 窗口大小的复杂 STFT 表示，从而得到 256 个频率 bin、128 的跳跃大小和周期为汉明窗口。我们在每个训练步骤中随机裁剪 STFT 表示的长度为 256 帧。为了补偿 STFT 语音幅度通常呈重尾分布的情况 [19]，我们按照 [8] 的方法，通过 β|c| α e i∠(c) 的变换处理 STFT 表示的每个复数系数 c，其中 β=0.15，α=0.5。

4.3 采样和度量

为了公平比较基准 OUVE SDE 和提出的 BBED SDE，我们使用相同的采样器设置。我们使用预测-校正方案，如[8, 11]中所示，其中预测器是欧拉-马鲁雅马方法，而校正器是退火 langevin 动力学（ALD）方法。与[8]中一样，ALD 的步长选择为 0.5，反向步数为 30。等效地，反向过程中的步长为 h = T / 30，其中 T 分别针对 OUVE SDE 和 BBED SDE 设置（见第 4.4 节）。对于反向过程，我们将反向起始时间设置为 trs = T。我们还在第 5.3 节中报告了在固定步长 h = T / 30 的情况下尝试反向起始时间 trs < T 时的结果。我们使用感知度量 PESQ[20] 和 POLQA[21]，以及能量度量 SI-SDR、SI-SIR 和 SI-SAR[22] 来评估性能。

4.4 OUVE 和 BBED

图2：黑色和蓝色曲线是WSJ0-CHiME3测试集BBED和OUVE平均演化（15）中定义的平均∆信噪比（µ(t)）。黄色虚线是y的信噪比。OUVE SDE用γ = 1.5参数化，如第4.4节所述。 

5 结果

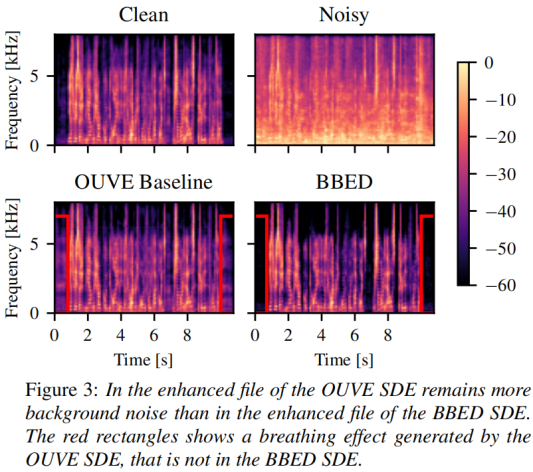
6 结论

在本文中，我们的目的是最小化基于分数的生成建模的先验不匹配的语音增强。为此，我们建造了受布朗桥启发的BBED SDE。与基线OUVE SDE相比，BBED SDE产生的先验不匹配要小得多，并且只有一个需要调优的超参数。因此，与OUVE SDE相比，我们不断地改进了所有报告的指标。此外，BBED SDE在PESQ中提高了0.13，在POLQA中提高了0.26，即使只使用了只有OUVE SDE一半的函数评估。