十四届蓝桥杯-统计子矩阵

题目

给定一个 N×M的矩阵 A，请你统计有多少个子矩阵 (最小 1×11×1，最大 N×M) 满足子矩阵中所有数的和不超过给定的整数 K?

输入格式

第一行包含三个整数 N,M和 K。

之后 N行每行包含 M个整数，代表矩阵 A。

输出格式

一个整数代表答案。

数据范围

对于 30%30% 的数据，N,M≤20，
对于 70%70% 的数据，N,M≤100，
对于 100%100% 的数据，1≤N,M≤500;0≤Aij≤1000;1≤K≤2.5×10^8

输入样例：

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

输出样例：

19

样例解释

满足条件的子矩阵一共有 1919，包含：

• 大小为 1×11×1 的有 1010 个。
• 大小为 1×21×2 的有 33 个。
• 大小为 1×31×3 的有 22 个。
• 大小为 1×41×4 的有 11 个。
• 大小为 2×12×1 的有 33 个。

分析：

1.直接暴力枚举，O(n^6)

2.优化：使用二维前缀和+暴力O(n^2+m^2)

3.继续优化：降维+双指针

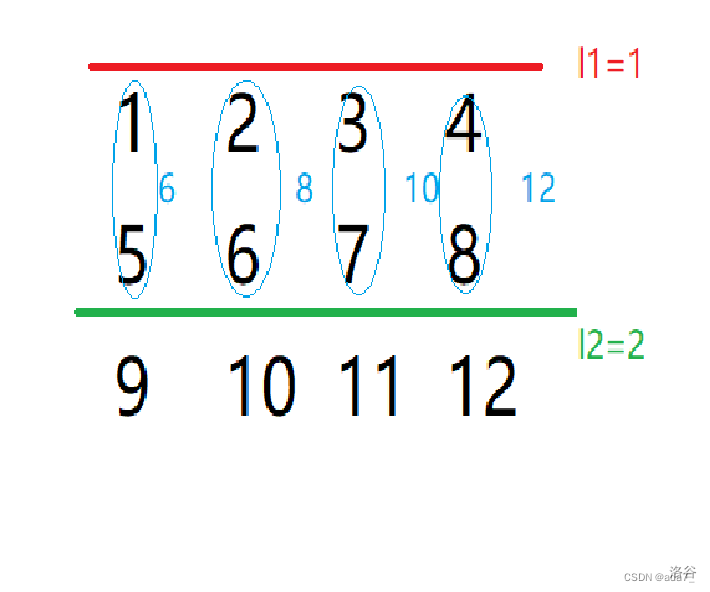
（1）假设有两条线如图分割整个矩阵，枚举这两条线可能出现的位置O(n^2)

（2）把每一列看成一个整体，如下图，将问题求解的 子矩阵 转换成 子序列

（3）求解子序列中和<=k的个数：

        （1）暴力：两重循环，显然不行，会超时

        （2）双指针（解决线性序列问题）：快慢指针

当sum[l,r] <= k时，l + 1 <= r时，sum[l+1,r] < k，所以只要l.....r的和<=k，那么其中间的数到r都<=k，cnt += r - l + 1;

当sum[l,r] >k 时，将l ++，直到和<=k

注意点：

根据数据范围可知，最终的答案可能会爆int（确实会...），所以要用long long

代码

#include<iostream>
using namespace std;

const int N = 510;
typedef long long ll;
int a[N][N],s[N][N],b[N];
ll n,m,k;  //long long

int main()
{
	scanf("%lld %lld %lld",&n,&m,&k);
	for(int i = 1;i <= n;i ++)
		for(int j = 1;j <= m;j ++) scanf("%d",&a[i][j]);
	for(int i = 1;i <= n;i ++)
	{
		for(int j = 1;j <= m;j ++)
		{
			s[i][j] = s[i - 1][j] + a[i][j];  //固定行，处理每一列的和
		}
	}
	
	ll cnt = 0;
	for(int i = 1;i <= n;i ++)
	{
		for(int j = i;j <= n;j ++)
		{
			for(int col = 1;col <= m;col ++)
			{
				b[col] = s[j][col]-s[i-1][col];  //计算两条线中每一列的和
			}
            //双指针
			int l = 1,r = 1,sum = 0;
			for(;r <= m;r ++)
			{
				sum += b[r];
				if(sum <= k)
				{
					cnt += r - l + 1;
				}
				else
				{
					while(sum > k)
					{
						sum -= b[l];
						l ++;
					}
					cnt += r - l + 1;
				}
			}
		}
	}
	printf("%lld",cnt);
	return 0;
}