20230809模拟赛 T1题解-优快云博客

本文链接：https://blog.youkuaiyun.com/aaaalpy/article/details/132205238

文章讨论了在一个给定线段集合中找到两条具有公共点的线段，使得它们异或值最大的问题。作者首先提出暴力方法，随后优化为使用线段树数据结构，通过维护区间极值来求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题面

【问题描述】

utsuho有n条线段,现在她希望在其中找到两条有公共点的线段,使得它们的异或值最大。

定义线段异或值为它们并的长度减它们交的长度.

【输入格式】

从文件 ut.in 中读入数据。

输入的第一行包括一个正整数n,表示Utsuho的线段的个数。

接下来 n 行每行包括两个正整数l,r,表示Utsuho拥有的线段的左右端点。

【输出格式】

输出到文件 ut.out 中。

输出一行一个整数,表示能得到的最大异或值。

【样例输入1】

10 100

1 50

50 100

【样例输出1】

【样例说明】

选择第一条和第二条:99-40=59

选择第一条和第三条:90-50=40

选择第二条和第三条:99-0=99

【样例输入2】

1 100

180 200

190 210

【样例输出2】

思路

先读题，看到题里说要求任意有公共点的两条线段的异或值，首先想到两条线段一维的关系：包含，相交以及分离；

分离我们不用考虑，只需要维护相交和包含两种关系

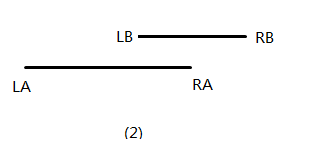
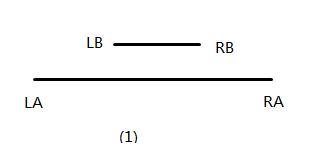
~~懒得画图了借用一下大佬的~~

包含：线段异或值=RA-LA-RB-LB
相交：线段异或值=RB-LA-RA+LB

暴力

考场上一开始想的是直接暴力，用伪 $O\left ( n^{2} \right )$ 的做法直接维护两种关系然后取max

思路还是比较好想的

上代码（其中 x，y为l，r）

#include<cstdio>
#include<algorithm>
using namespace std;
namespace jdy{signed main();}
signed main(){return jdy::main();}
namespace jdy
{
	struct node
	{
		int x,y;
	}nd[200001];
	int n;
	int maxn=-1000;
	int ans=0;
	signed main()
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++)	
		{
			scanf("%d%d",&nd[i].x,&nd[i].y);	
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=i+1;j<=n;j++)
			{
				if(nd[i].y>=nd[j].x)
				{
					ans=(nd[j].y-nd[i].x)-(nd[i].y-nd[j].x);
					maxn=max(maxn,ans);
				}
				if(nd[i].y>=nd[j].y)
				{
					ans=(nd[i].y-nd[i].x)-(nd[j].y-nd[j].x);
					maxn=max(maxn,ans);	
				}
			}
		}
		printf("%d",maxn);
		return 0;
	}
}

正解

显然这个暴力是会TLE的

所以我们现在来想如何更优

首先类似这种同时处理l，r且有很多线段，二维偏序问题，想到先按左端点排序

分析一下：我们前面推出了包含和相交两种关系的式子

包含：线段异或值=RA-LA-RB+LB
相交：线段异或值=RB-LA-RA+LB

整理一下得RA-LA+LB-RB和LB+RB-LA-RA

不难发现我们要求最大值，只需要维护一个(LB-RB)最大和一个(LB+RB)最大

求极值转换为求另一部分的极值，又要满足有公共点（即区间极值），想到数据结构线段树

我们可以在线段树中维护一个sum1为(LB+RB），一个sum2为LB-RB)；

那么每次我们只需要求一下max就行了

最后将所有边加入后二分求极值

上代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define INF 0x3f3f3f3f
int maxx1[200005*4];
int maxx2[200005*4];
int ans1,ans2;
struct Node{
   int x;
   int y;
}nd[200005];
bool cmp(Node a,Node b)
{
   if(a.x!=b.x)
    return a.x<b.x;
   return a.y<b.y;
}
struct tree
{
    int l;
    int r;
    int sum1,sum2;
}tr[200005*4];
void pushup(int rt)
{
  tr[rt].sum1=max(tr[rt<<1].sum1,tr[rt<<1|1].sum1);
  tr[rt].sum2=max(tr[rt<<1].sum2,tr[rt<<1|1].sum2);
}
void build(int l,int r,int rt)
{
    tr[rt].l=l;
    tr[rt].r=r;
    if(l==r)
    {
      tr[rt].sum1=nd[l].x+nd[l].y;
      tr[rt].sum2=nd[l].x-nd[l].y;
      return;
    }
    int mid=(tr[rt].l+tr[rt].r)/2;
    build(l,mid,rt<<1);
    build(mid+1,r,rt<<1|1);
    pushup(rt);
}
 
void query(int l,int r,int rt)
{
    if(tr[rt].l==l&&tr[rt].r==r)
    {
      ans1=max(ans1,tr[rt].sum1);
      ans2=max(ans2,tr[rt].sum2);
      return;
    }
    int mid=(tr[rt].l+tr[rt].r)/2;
    if(r<=mid)query(l,r,rt<<1);
    else if(l>mid)query(l,r,rt<<1|1);
    else
    {
        query(l,mid,rt<<1);
        query(mid+1,r,rt<<1|1);
    }
    pushup(rt);
}
int main()
{
//	freopen("ut.in","r",stdin);
//	freopen("ut.out","w",stdout);
	int n,ans=0;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d%d",&nd[i].x,&nd[i].y);
	sort(nd+1,nd+n+1,cmp);
	build(1,n,1);
	for(int i=1;i<=n;i++)
	{
		int le=i;
		int rr=n+1;
		while(le+1<rr)
		{
			int mid=(le+rr)/2;
			if(nd[mid].x<=nd[i].y)
			le=mid;
			else
			rr=mid;
		}
		if(le==i)continue;
		ans1=-INF;
		ans2=-INF;
		query(i+1,le,1);
		ans=max(ans,ans1-nd[i].x-nd[i].y);
		ans=max(ans,nd[i].y-nd[i].x+ans2);
	}
	printf("%d\n",ans);
	return 0;
}

~~ok本蒟蒻只会这道题了~~