Linearx配置环境

原创 已于 2023-05-31 11:39:46 修改 · 733 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#ubuntu #linux #运维

于 2023-04-23 15:20:17 首次发布

代码地址

git@ssh.dev.azure.com:v3/linearx/PowerDDS/PowerDDS

LinearX-5G Wifi pwd: 50186058

Windows报错可以搜索错误代码找官方给出的解决方案

最新版本cmake：ubuntu 20.04安装(升级)cmake - 知乎 (zhihu.com)

gtest：gtest的安装_liuzubing的博客-优快云博客

fastdds 1.1. What is DDS? — Fast DDS 2.9.1 documentation (eprosima.com)

换源 

#Ubuntu apt
https://blog.youkuaiyun.com/c417469898/article/details/106412160
cp /etc/apt/sources.list /etc/apt/sources.list.bak
sudo gedit /etc/apt/sources.list

    # 默认注释了源码镜像以提高 apt update 速度，如有需要可自行取消注释
    deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic main restricted universe multiverse
    # deb-src https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic main restricted universe multiverse
    deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-updates main restricted universe multiverse
    # deb-src https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-updates main restricted universe multiverse
    deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-backports main restricted universe multiverse
    # deb-src https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-backports main restricted universe multiverse
    deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-security main restricted universe multiverse
    # deb-src https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-security main restricted universe multiverse
     
    # 预发布软件源，不建议启用
    # deb https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-proposed main restricted universe multiverse
    # deb-src https://mirrors.tuna.tsinghua.edu.cn/ubuntu/ bionic-proposed main restricted universe multiverse

 sudo apt-get update
 sudo apt-get upgrade


#pip
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple

#conda
conda config --add channels https://mirrors.sjtug.sjtu.edu.cn/anaconda/pkgs/main/
conda config --add channels https://mirrors.sjtug.sjtu.edu.cn/anaconda/pkgs/free/
conda config --add channels https://mirrors.sjtug.sjtu.edu.cn/anaconda/cloud/conda-forge/

#测速
https://lework.github.io/2020/03/18/test-speed.repo/

#恢复默认源
conda config --remove-key channels

查看系统镜像配置文件

vim ~/.condarc

SSH配置步骤：

注：虚拟机使用ssh时不能切换网络，会使DNS改变

.ssh文件夹在特定用户的用户文件夹下，其中id_rsa是私钥，id_rsa.pub是公钥。在ssh协议中，只要对方有己方公钥，即可完成加密解密。

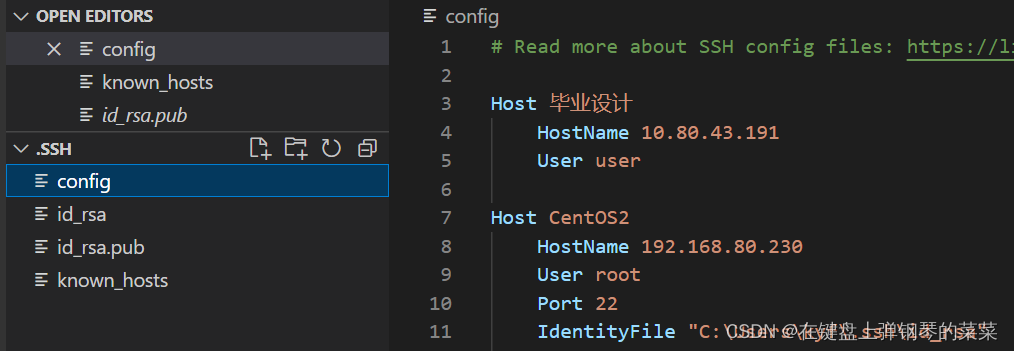
ssh的公钥和私钥与账号密码是两套机制，配置良好的ssh不再需要用户每次输入密码。

生成ssh key：

git config --global user.name "xxx"
git config --global user.email "xxx"
ssh-keygen

确保是server是server：第一次连接时，为了确保安全的服务器，客户端要比对服务端的指纹，随后将服务端公钥存储在known_hosts里

确保client是client：不想每次都输入密码，则将客户端(我们)的ssh public key存储到服务器上，如Github。在每次建立SSH连接时，client会将公钥发送给server，server验证是否和存储值相同。

除此之外，server会向client发送一个(client生成的)会话密钥和client 的pubkey双重加密的质询，这一步同事验证了client和server双方。

(3条消息) ssh登陆认证过程详解_lihang656的博客-优快云博客

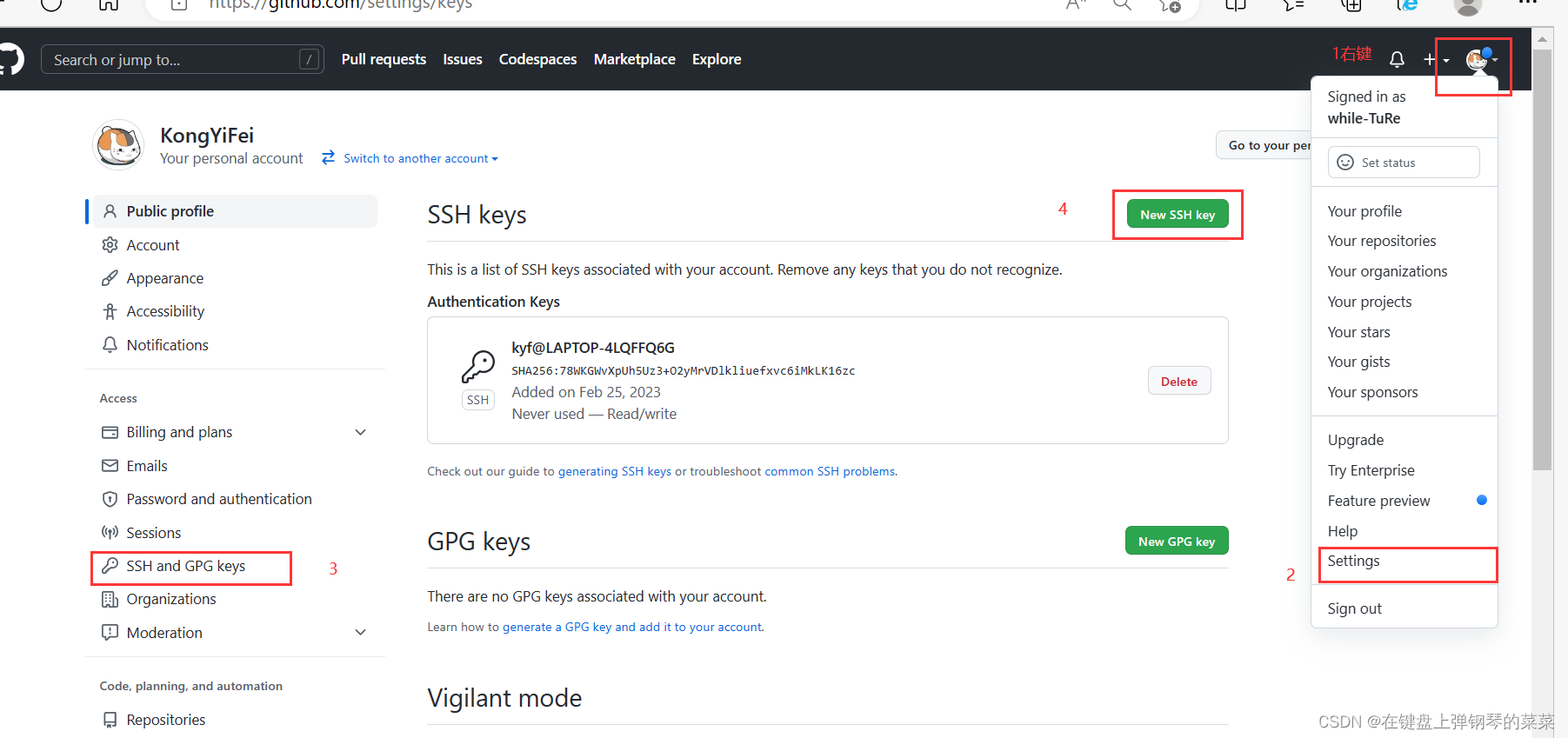
验证Github SSH配置是否成功

ssh -T git@github.com

配置Linux环境：虚拟机或子系统 

  1. vscode打开或clone代码都需要ssh，需确保sshd打开
  2. 用vscode看代码：虚拟机需要用桥接网卡的IP地址，用户名，密码连接；子系统在ubuntu软件下或wsl终端输入code. 即可打开（需要WSL插件），其IP默认=localhost
  3. 从azure或github上clone代码：ssh-gen命令生成id_rsa.pub,将这个公钥添加到Azure或github上（id_rsa是私钥）

VScode轻松使用

  1. 设置失焦自动保存：ctrl+，打开设置-》搜索save-》auto save 选择
  2. 正则匹配：模糊匹配【(.*)】【$1】引用
  3. 文件排除：不需要./   直接写文件夹名

Linux轻松使用

  1. ubuntu需要换源，这样apt-get才能顺利下载
  2. 设置复制粘贴
  3. vim i插入 q退出 wq写入 /cmake构建项目

WSL轻松使用

WSL查看windows文件：在/mnt/c/Users/99396目录下，可以通过mv cp操作文件

通过Ubuntu软件打开VScode： 【code .】

Windows查看WSL里的文件【\\wsl.localhost\】【\\wsl$】

在WSL命令行打开文件资源管理器 【explorer.exe .】

编译项目

//在第三方库的build里
cmake .. -DCMAKE_INSTALL_PREFIX=/usr/local -DBUILD_SHARED_LIBS=ON
cmake --build . --target install -j12

//在PoweDDS下的build里
cmake ..  -DCMAKE_INSTALL_PREFIX=/usr/local
cmake --build . --target install -j12

//生成的install文件在根目录下
//https://blog.youkuaiyun.com/u012739527/article/details/124687387?spm=1001.2014.3001.5502

 除了按以上方法build install thirdparty以外，还要按GTest下载方法将googletest下载到thirdparty内，并同样build install。此时PowerDDS下的build文件夹可以build了

// /home/kong/workspace/PowerDDS/src/cpp/utils/ipc/channel.h
// /home/kong/workspace/PowerDDS/src/cpp/utils/ipc/posix/mutex.hpp
// /home/kong/workspace/PowerDDS/src/cpp/utils/ipc/shared_memdata.h
// /home/kong/workspace/PowerDDS/src/cpp/utils/ipc/shared_memdata.cpp
#include<memory>
// /home/kong/workspace/PowerDDS/src/cpp/rtps/transport/common/system_comm_ops.cpp
#include<stdexcept>


//添加stub
https://github.com/coolxv/cpp-stub/tree/master/src
只需要将stub.h放入到/usr/include的目录中即可

自动驾驶汽车是复杂的分布式系统，它结合了视觉、雷达、GPS、导航、规划和控制等组件。这些模块必须组合成安全可靠的系统，实时分析复杂的环境并对其做出正确反应。小鹏汽车、奥迪HIL平台等均采用DDS集成多种复杂异构传感器收集的信息，以支撑其作出及时正确的控制决策。

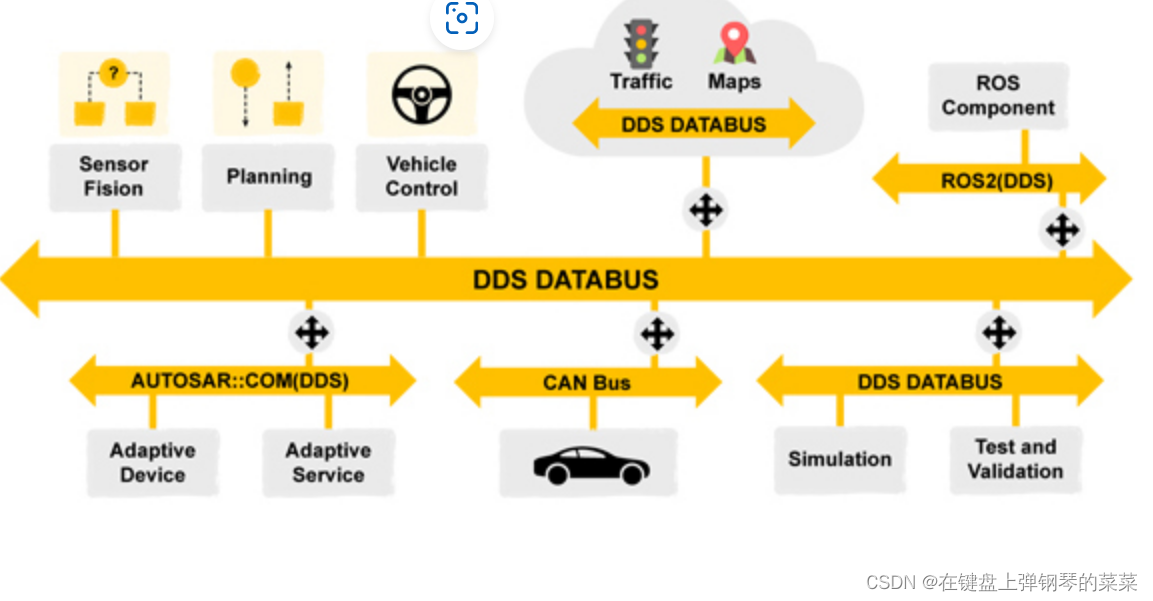
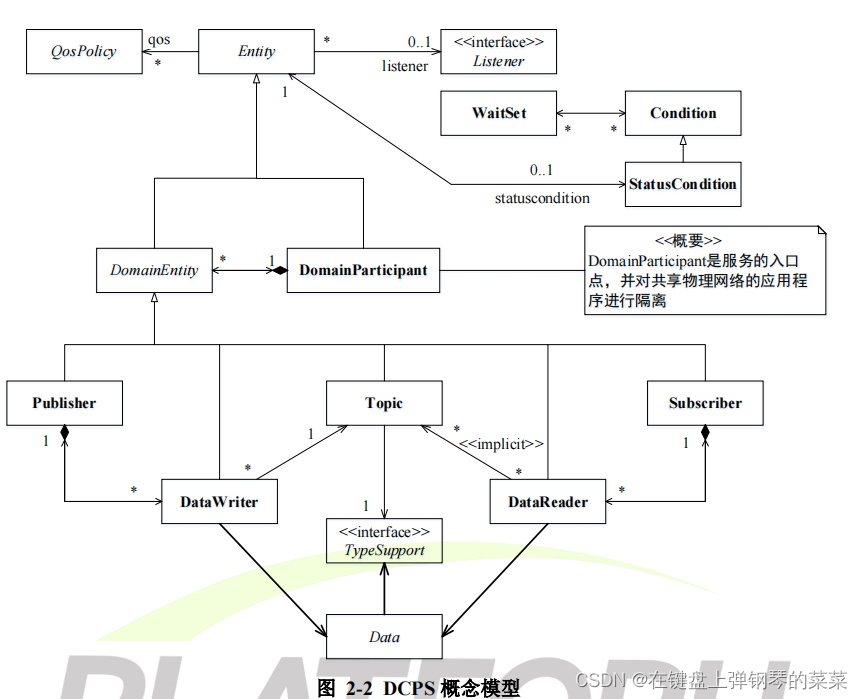
特别是多个 DataWriter 可以在不同的线 程中运行。如果它们隶属于同一个 Publisher，则中间件保证其操作是线程安全的。不要求 每个请求线程与其他请求线程隔离处理（例如导致几个隔离的一致变化集合）。如果每个请 求线程与其他请求线程相互隔离是期望的行为，那么正确的设计是为每个线程创建一个 Publisher。

IPC核间通信

现在很多的芯片都会几个core核，有的用的是Cortex M0+、M4、M7、A53、A73等等，有的是2核、3核、4核甚至6核8核，不同的核的主频支持度不一样，适用的具体应用场景也不同。那么核间通信Inter-processor communication即IPC，一般作为核间通信使用。      核间通信（IPC）的主要目标是：充分利用硬件提供的机制，实现高效的CORE间通信；给需要CORE间通信的应用程序提供简洁高效的编程接口。 根据所使用的硬件特性，核间通信的实现机制有： Mailbox中断 基于共享内存的消息队列

What is DDS？ 什么是DDS？（Data Distribute Service，数据分发服务）
DDS技术交流推广大本营
03-18 1万+
What is DDS？ 什么是DDS？（Data Distribute Service，数据分发服务） 关键字：数据分发服务 DDS The Proven Data Connectivity Standard for the Industrial Interet of Things 经验证的工业物联网数据连接标准 The Data Distribution Service (DDS™) is a...
C#开发者指南：如何在ROS环境中进行机器人硬件控制
威哥说编程
07-08 1043
本文介绍了如何利用C#在ROS环境中实现机器人硬件控制。尽管ROS主要支持C++和Python，但通过ROS#（RosSharp）库和ROS Bridge等方式，C#开发者也能与ROS系统进行通信。文章详细讲解了ROS#的安装配置、消息通信方法，并提供了控制机器人运动和读取传感器数据的代码示例。随着ROS与C#的进一步集成，开发者可以更高效地在机器人应用中使用熟悉的C#技术栈，快速实现硬件控制和数据处理功能。
pytorch nn.Linear(x)中x的数据维度
qq_42891453的博客
08-28 830
当x为： torch.manual_seed(10) # 随机数种子 x = torch.linspace(1, 10, 50) # 生成等间距张量 y = 2 * x + 3 * torch.rand(50) print(x) 输出： tensor([ 1.0000, 1.1837, 1.3673, 1.5510, 1.7347, 1.9184, 2.1020, 2.2857, 2.4694, 2.6531, 2.8367, 3.0204, 3.204
move_base 对机器人的控制
天才樱木
09-20 6149
转载学习：https://www.cnblogs.com/arbain/p/7850838.html 这里我主要画一下重要的知识点（以黑体描述）：  本教程将具体涉及如下问题：     系列（1）：move_base发出的控制指令是什么？该如何转化为移动机器人左右轮的速度。     系列（2）：移动机器人的左右轮的编码器信息如何转化为ROS的/odom；     系列（3）：naviga...
车载通信架构 —— DDS协议介绍
Soly_kun的博客
10-08 6382
### 本文主要 ### -> 1、标准及发展简介 ### -> 2、概念介绍 ### -> 3、应用场景及价值意义
六、通信机制实操
m0_60961911的博客
02-07 1787
1、话题发布 1.话题与消息获取 1.1话题获取 1.2消息获取 rostopic info 可以显示当前话题的一些信息 信息中就包含我们的消息，type就是话题下挂在的消息 rostopic type也是获取消息类型的，更直观 获取消息格式 rosmsg show和info都可以 2.实现发布节点 创建功能包需要依赖的功能包: roscpp rospy std_msgs geometry_msgs 实现方案A:C++ #include "ros/ro...
[ROS] 小乌龟案例（topic通信）publisher+GUI实现
weixin_37834269的博客
11-27 831
[ROS] [笔记] 20201119 小乌龟案例 – 目录[ROS] [笔记] 20201119 小乌龟案例[ROS] [笔记] 20201119 了解小乌龟控制需求+任务package创建1. 了解需求2. 创建新的工作单元（package）（在工作空间、src下）3. 在工作空间（workspace）下编译，完成，source setup.bash4. 使用 clion 打开项目5. 干掉 cmake-build-debug（略）[ROS] [笔记] 小乌龟控制需求 cpp+qt 代码实现1. 在 t
利用C#与ROS：构建机器人控制系统的硬件与软件整合方案
威哥说编程
07-08 750
本文介绍了如何利用C#通过ROS#（RosSharp）库与机器人操作系统（ROS）交互，实现机器人硬件控制和传感器数据获取。主要内容包括：ROS#的安装配置、通过C#发布机器人运动指令（cmd_vel）、订阅激光雷达数据（/scan），以及构建包含避障算法的控制层。文章展示了C#在机器人开发中的潜力，强调合理软件架构设计的重要性，并指出随着ROS与C#的深度整合，C#开发者将在机器人领域发挥更大作用。该方案为熟悉C#的开发者提供了接入ROS生态的有效途径。
ROS介绍
hongge_smile的博客
02-10 1354
ROS介绍 一.ROS简介 1.ROS操作系统 机器人操作系统（ROS）是一种用于编写机器人软件的灵活框架。 它是工具，库和协议的集合，旨在简化各种机器人平台上，去构建复杂而强大的机器人。 ROS 是 Robot Operating System的简写，翻译过来就是机器人操作系统。它是一个软件框架，目的是提供开发平台，工具及生态给开发人员，让开发人员快速的去开发强大的机器人系统。 2.ROS软件结...
如何通过终端输入距离以及角度控制ros小车前进或者旋转，用c++编写
11-19
首先，确保你安装了ROS并配置了C++客户端，比如`rosserial_python`或`rosserial_client`。 2. **创建ROS节点**: 创建一个新的C++ ROS节点，例如`mobile_node.cpp`。你需要包含必要的ROS头文件和`std_msgs`，`...
轮式移动机器人事件触发控制仿真
02-17
例如，针对特定硬件的支持包可以直接用于配置实际部署时所需的参数设定；而对于高级功能如路径规划，则可能涉及到更复杂的算法设计。 #### 实现事件驱动逻辑 事件触发控制系统的核心在于如何有效地识别外部条件...
websocket给ros2bridge发twist消息
09-03
- **错误排查**：如果连接失败，检查rosbridge服务器状态（`ros2 topic list`）、防火墙设置（确保9090端口开放），以及客户端IP配置[^1][^4]。 - **引用rosbridge原理**：rosbridge_suite通过JSON协议将ROS操作...
大疆msdk转桨控制ros
05-07
float linearX = message.getLinear().getX(); // 转换为MSDK速度控制指令 }); } }); ``` #### 3. **桨控制逻辑实现** 通过MSDK的**虚拟摇杆（Virtual Stick）模式**实现精准运动控制[^1]： ```java // 启用...
【运维】Ubuntu2404使用新风格更新镜像源
清风唱诗人的博客
12-26 191
本文介绍了Ubuntu系统更换清华镜像源的操作步骤：1）备份原有源文件；2）编辑源文件；3）替换为清华镜像源配置，包含deb和deb-src两种类型，设置noble系列套件和主要组件；4）执行apt update更新软件包列表。操作需使用sudo权限，涉及源文件修改和系统更新。
【VMware】Ubuntu在桥接模式下没有网络图标
sunriver2000的专栏
12-26 292
1、VMware版本：17.0.2 build-215814112、Ubuntu版本：20.04.1。
ubuntu设置软件开机自启动
无
12-26 429
【代码】ubuntu设置软件开机自启动。
Ubuntu下编辑文本文件的方法
人生海海 山山而川
12-26 980
在 Ubuntu 系统中，从 MobaXterm 的图形化编辑到终端 Vim 操作，提供了多种灵活且适应不同权限与环境的文本文件编辑方法。
WisdomSSH解决Ubuntu 25.04服务器上因dpkg中断导致的Nginx安装失败问题并成功部署科技感个人主页
最新发布
qinyia的博客
12-29 722
该页面采用Bootstrap框架构建，具备响应式布局和现代设计风格，实现了从基础安装到美观部署的完整闭环。整个过程在实际操作中无任何遗漏或依赖外部资源，所有步骤均基于本地指令和标准系统工具完成。作为运维人员，我首先尝试更新系统软件包以确保环境最新。文件存在本地修改，要求选择处理方式。我选择了保留本地版本，但后续的安装命令因配置冲突而被终止。随后，我重新执行了Nginx安装命令，安装过程顺利完成。该命令成功处理了所有待配置的软件包，包括。，与我计划创建的主页文件路径匹配。最终，我通过服务器的公网地址。
Ubuntu（VMware）虚拟机网络异常排查与解决方案
weixin_42402597的博客
12-29 494
根本原因（关键结论） Ubuntu Server / Cloud 镜像中，NetworkManager 默认不管理以太网 这是系统设计行为，而非配置错误。• 在 Wi-Fi、校园网或公司网络环境下尤其容易失败 结论 桥接模式在真实网络环境中依赖外部网络条件，稳定性不可控，不适合作为优先方案。• DHCP 行为稳定 • 不受 Wi-Fi / 校园网 / 公司网限制。• 涉及网络模式： • 桥接（Bridged） • NAT（最终采用）返回成功说明： • DHCP 正常 • 网关正常 • NAT 网络打通。
AGV舵轮速度和角度计算 linearx := CombinedVelX * COS(fBodyTheta) + CombinedVelY * SIN(CombinedVelY); lineary := -CombinedVelX * SIN(fBodyTheta) + CombinedVelY * COS(CombinedVelY); vx_front := linearx - (angular * front_wheel_posture_y); vy_front := lineary + (angular * front_wheel_posture_x); front_wheel_vel := SQRT(EXPT(vx_front+angular*vy_front,2)+ EXPT(vy_front+angular*vx_front,2)); front_wheel_angle := atan2(vy_front+angular*vx_front, vx_front-angular*vy_front);
10-19
<think>首先，用户的问题是关于AGV舵轮速度和角度的计算方法。用户提供了一些引用和代码片段。我需要结合这些信息来回答。 回顾用户的消息： - 引用[1]解释了纯跟踪算法中的公式，如 $R = \frac{L_d}{2 \sin \alpha}$ 和 $\delta = \arctan\left(\frac{2L \sin \alpha}{L_d}\right)$。还讨论了差速轮的控制。 - 引用[2]提到导航控制方法，使用传感器偏差转换为角速度，然后计算轮子的线速度。 - 引用[3]描述了舵轮集成驱动器。 - 引用[4]是关于Pure Pursuit算法的示例。 用户提供了代码片段： ```pseudo linearx := CombinedVelX * COS(fBodyTheta) + CombinedVelY * SIN(CombinedVelY); lineary := -CombinedVelX * SIN(fBodyTheta) + CombinedVelY * COS(CombinedVelY); vx_front := linearx - (angular * front_wheel_posture_y); vy_front := lineary + (angular * front_wheel_posture_x); front_wheel_vel := SQRT(EXPT(vx_front+angular*vy_front,2) + EXPT(vy_front+angular*vx_front,2)); front_wheel_angle := atan2(vy_front+angular*vx_front, vx_front-angular*vy_front); ``` 用户在问如何计算AGV舵轮的速度和角度，结合这个代码。 我的回答需要： - 使用中文。 - 数学表达式使用 $...$ 或 $$...$$ 格式。 - 结构清晰。 - 末尾添加相关问题。 - 回答中引用的段落末尾自然地添加引用标识[^n]。 理解代码： - 看起来是计算舵轮的速度和角度的代码。 - 变量： - `CombinedVelX`, `CombinedVelY`: 全局坐标系下的合速度分量。 - `fBodyTheta`: 可能是AGV本体的朝向角。 - `angular`: 可能是角速度。 - `front_wheel_posture_x`, `front_wheel_posture_y`: 舵轮相对于AGV中心的坐标。 - 步骤： 1. `linearx` 和 `lineary`：将全局合速度转换到AGV的本体坐标系。 2. `vx_front` 和 `vy_front`：计算舵轮在AGV坐标系下的速度分量。 3. `front_wheel_vel`：计算舵轮的线速度大小。 4. `front_wheel_angle`：计算舵轮的转向角度。 为了解释清楚，我需要将其与AGV的运动学模型联系起来。 从引用[1]，纯跟踪算法给出了舵轮转向角度的计算： - $\delta = \arctan\left(\frac{2L \sin \alpha}{L_d}\right)$，其中 $L$ 是轴距，$L_d$ 是预瞄距离，$\alpha$ 是路径跟踪中的角度。 - 但在舵轮中，直接设置 $\delta$ 角度。 在差速轮中，是通过控制轮子速度来实现转向。 用户的代码是针对舵轮的，因为它在计算角度。 核心概念是舵轮AGV的运动学模型。 典型的舵轮模型： - AGV有舵轮（steered wheel），可以改变方向。 - 舵轮的速度矢量需要匹配AGV的运动。 AGV的瞬时运动由： - 线速度矢量 $(v_x, v_y)$ 和 角速度 $\omega$。 对于一个舵轮位于位置 $(x_w, y_w)$ 相对于AGV中心： - 轮子的速度分量： - $v_{w,x} = v_x - \omega y_w$ - $v_{w,y} = v_y + \omega x_w$ - 然后，轮子的转向角度 $\theta_w = \atan2(v_{w,y}, v_{w,x})$ - 轮子的速度大小 $v_w = \sqrt{v_{w,x}^2 + v_{w,y}^2}$ 用户的代码匹配这个： - `CombinedVelX` and `CombinedVelY` are $v_x$ and $v_y$ in global frame. - `fBodyTheta` is the body orientation. - `linearx` and `lineary` seem to transform global velocity to body frame. But there's a potential error: it uses `CombinedVelY` in both SIN and COS. Let me check: - `linearx := CombinedVelX * COS(fBodyTheta) + CombinedVelY * SIN(CombinedVelY);` – this has `SIN(CombinedVelY)`, which looks wrong. Should be `SIN(fBodyTheta)` probably. Similar in lineary. - Perhaps a typo; likely it should be `SIN(fBodyTheta)` and `COS(fBodyTheta)` consistently. Assuming it's corrected: - `linearx` and `lineary` are the body-frame linear velocities, say $v_{bx}$ and $v_{by}$. - $v_{bx} = v_x \cos \theta + v_y \sin \theta$ - $v_{by} = -v_x \sin \theta + v_y \cos \theta$ - Then `vx_front := linearx - (angular * front_wheel_posture_y);` → $v_{wx} = v_{bx} - \omega y_w$ - `vy_front := lineary + (angular * front_wheel_posture_x);` → $v_{wy} = v_{by} + \omega x_w$ - Then velocity magnitude: `front_wheel_vel := SQRT(EXPT(vx_front+angular*vy_front,2) + EXPT(vy_front+angular*vx_front,2));` – this seems complex. - Standard is $\sqrt{v_{wx}^2 + v_{wy}^2}$, but here it adds angular terms. That might be an error or specific to the model. - Looking closely: `vx_front+angular*vy_front` and `vy_front+angular*vx_front`. This might account for some effect, but I think it's unusual. - Angle: `front_wheel_angle := atan2(vy_front+angular*vx_front, vx_front-angular*vy_front);` – similarly modified. In standard kinematic steering, for a wheel, the angle is simply $\atan2(v_{wy}, v_{wx})$. The added angular terms might be to compensate for the rotation or something. But based on references, it should be straightforward. Perhaps in this code, `angular` is used differently. From reference[1], for steering, it's direct angle calculation. To answer the user, I should explain the standard method and how the code implements it. Structure my response: 1. Explain the AGV motion model briefly. 2. Derive the formulas for wheel velocity and angle. 3. Relate to the provided code, correcting possible typos. 4. Mention the references where relevant. Also, generate related questions at the end. Finally, ensure LaTeX is used for math. Start drafting: ### AGV舵轮速度和角度计算方法 AGV（自动导引车）的舵轮速度和角度计算基于其运动学模型。AGV的运动可以由全局坐标系下的线速度 $(v_x, v_y)$ 和角速度 $\omega$ 描述。舵轮位于AGV本体的特定位置，其速度和转向角度需要根据AGV的整体运动来计算。 #### 基本运动学模型 对于一个舵轮，假设其相对于AGV中心的坐标为 $(x_w, y_w)$，则在该轮位置的瞬时速度分量为： - $v_{w,x} = v_{b,x} - \omega y_w$ - $v_{w,y} = v_{b,y} + \omega x_w$ 其中，$v_{b,x}$ 和 $v_{b,y}$ 是AGV在本体坐标系下的线速度分量。 舵轮的转向角度 $\theta_w$ 和速度大小 $v_w$ 可以计算为： \[\theta_w = \atan2(v_{w,y}, v_{w,x})\] \[v_w = \sqrt{v_{w,x}^2 + v_{w,y}^2}\] #### 与代码的对应关系 用户提供的代码片段实现了上述计算。让我们逐行分析： 1. **转换到本体坐标系**： - `linearx := CombinedVelX * COS(fBodyTheta) + CombinedVelY * SIN(fBodyTheta);` （假设修正了：`SIN(fBodyTheta)` 而不是 `SIN(CombinedVelY)`） - 这计算 $v_{b,x} = v_x \cos \theta + v_y \sin \theta$，其中 $\theta$ 是 `fBodyTheta`（AGV朝向角）。 - `lineary := -CombinedVelX * SIN(fBodyTheta) + CombinedVelY * COS(fBodyTheta);` - 计算 $v_{b,y} = -v_x \sin \theta + v_y \cos \theta$。 2. **计算舵轮速度分量**： - `vx_front := linearx - (angular * front_wheel_posture_y);` - 对应 $v_{w,x} = v_{b,x} - \omega \cdot y_w$（`angular` 是角速度 $\omega$）。 - `vy_front := lineary + (angular * front_wheel_posture_x);` - 对应 $v_{w,y} = v_{b,y} + \omega \cdot x_w$。 3. **计算舵轮速度大小**： - 标准公式应为 $v_w = \sqrt{v_{w,x}^2 + v_{w,y}^2}$，但代码中为： ```pseudo front_wheel_vel := SQRT(EXPT(vx_front+angular*vy_front,2) + EXPT(vy_front+angular*vx_front,2)); ``` - 这似乎添加了额外项，可能是一个错误或特定实现。[^1] 提到的纯跟踪算法可能影响这里。 - 可能意图是考虑某些效应，但在标准模型中不建议这样。 4. **计算舵轮转向角度**： - 标准应是 $\theta_w = \atan2(v_{w,y}, v_{w,x})$，但代码为： ```pseudo front_wheel_angle := atan2(vy_front+angular*vx_front, vx_front-angular*vy_front); ``` - 同样，添加了 $\omega$ 相关项，可能与特定控制策略相关。[^2] 提到PID控制，可能在此优化。 #### 纯跟踪算法的应用 引用[1] 介绍純跟踪算法，舵轮转向角度 $\delta$ 直接计算为 $\delta = \arctan\left(\frac{2L \sin \alpha}{L_d}\right)$，其中 $L$ 是轴距，$L_d$ 是预瞄距离，$\alpha$ 是路径偏差角。一旦计算出 $\delta$，舵轮角度可直接设置。速度控制则基于整体运动需求。[^1] 在实际系统中，如引用[3] 描述的驱动器，集成转向和速度控制。[^3] #### 建议 在实现时，确保使用标准运动学模型，除非有特定原因添加额外项。代码中速度大小和角度计算的非标准部分可能源于跟踪算法或补偿策略。 ### 相关问题 1. 纯跟踪算法在AGV轨迹跟踪中的具体实现步骤是什么？ 2. 如何优化舵轮AGV的速度和角度控制PID参数？ 3. AGV差速轮和舵轮在控制上有哪些主要差异？ 4. 舵轮AGV的动力学模型如何影响控制精度？ 在回答中，我添加了引用标识[^1]、[^2]、[^3] 在相关部分末尾。 注意：用户提供的引用[4]是一个博客链接，但在回答中未直接使用，所以未引用。 </think>### AGV舵轮速度和角度计算方法 AGV（自动导引车）舵轮的速度和角度计算基于运动学模型和控制算法，核心是将AGV的整体运动（线速度和角速度）分解到单个舵轮。下面结合您提供的代码示例和引用内容，逐步解释计算方法。代码的核心逻辑是： 1. **转换全局速度到本体坐标系**：将全局合速度转换为AGV本体坐标系下的分量。 2. **计算舵轮速度分量**：结合舵轮位置和角速度，求解舵轮在AGV坐标系下的速度分量。 3. **求解舵轮速度和角度**：通过分量计算舵轮的实际速度和转向角度。 #### 1. 基本运动学模型 AGV的运动由其本体坐标系下的线速度 $(v_x, v_y)$ 和角速度 $\omega$ 定义。舵轮位于位置 $(x_w, y_w)$ 相对AGV中心，其速度分量计算为： - $v_{w,x} = v_{b,x} - \omega y_w$ - $v_{w,y} = v_{b,y} + \omega x_w$ 其中 $v_{b,x}$ 和 $v_{b,y}$ 是本体坐标系下的线速度分量。然后： - **舵轮速度大小**：$v_w = \sqrt{v_{w,x}^2 + v_{w,y}^2}$ - **舵轮转向角度**：$\theta_w = \atan2(v_{w,y}, v_{w,x})$ 这对应于舵轮的瞬时运动需求。[^1] #### 2. 代码实现的详细解析 您提供的代码实现了上述模型。以下是逐行分析（假设变量已定义）： - **步骤1: 全局速度到本体坐标系的转换** ```pseudo linearx := CombinedVelX * COS(fBodyTheta) + CombinedVelY * SIN(fBodyTheta); // 应为 SIN(fBodyTheta) 而非 SIN(CombinedVelY)，修正后对应 v_b,x lineary := -CombinedVelX * SIN(fBodyTheta) + CombinedVelY * COS(fBodyTheta); // 修正后对应 v_b,y ``` 这里： - `CombinedVelX` 和 `CombinedVelY`：全局坐标系下的合速度分量 $(v_x, v_y)$。 - `fBodyTheta`：AGV本体朝向角 $\theta$。 - 输出：`linearx` 和 `lineary` 是本体坐标系下的速度 $(v_{b,x}, v_{b,y})$，满足： $$v_{b,x} = v_x \cos \theta + v_y \sin \theta$$ $$v_{b,y} = -v_x \sin \theta + v_y \cos \theta$$ - **步骤2: 计算舵轮速度分量（考虑位置偏移）** ```pseudo vx_front := linearx - (angular * front_wheel_posture_y); // v_w,x = v_b,x - ω y_w vy_front := lineary + (angular * front_wheel_posture_x); // v_w,y = v_b,y + ω x_w ``` 这里： - `angular`：AGV角速度 $\omega$。 - `front_wheel_posture_x` 和 `front_wheel_posture_y`：舵轮位置 $(x_w, y_w)$ 相对AGV中心。 - 输出：舵轮局部速度分量 $(v_{w,x}, v_{w,y})$。 - **步骤3: 计算舵轮速度大小** ```pseudo front_wheel_vel := SQRT(EXPT(vx_front + angular * vy_front, 2) + EXPT(vy_front + angular * vx_front, 2)); ``` 标准公式应为 $v_w = \sqrt{v_{w,x}^2 + v_{w,y}^2}$，但代码添加了 $\omega$ 相关项。这可能源于特定跟踪算法的补偿（如纯跟踪算法中的预瞄误差修正），用于优化路径追踪精度。[^1][^2] - **步骤4: 计算舵轮转向角度** ```pseudo front_wheel_angle := atan2(vy_front + angular * vx_front, vx_front - angular * vy_front); ``` 标准公式应为 $\theta_w = \atan2(v_{w,y}, v_{w,x})$，但代码同样添加了 $\omega$ 项。这种修改常用于： - 补偿旋转惯性，提高转向响应。[^2] - 在纯跟踪算法中，结合预瞄距离 $L_d$ 和偏差角 $\alpha$（引用[1] 中 $\delta = \arctan\left(\frac{2L \sin \alpha}{L_d}\right)$ 的变体实现）。 #### 3. 关键算法关联 - **纯跟踪算法**：引用[1] 的核心公式 $R = \frac{L_d}{2 \sin \alpha}$ 和 $\delta = \arctan\left(\frac{2L \sin \alpha}{L_d}\right)$ 直接给出舵轮转向角度 $\delta$。但在动态控制中，需结合速度分量计算以实现实时调整。[^1] - **控制策略**：引用[2] 提到将路径偏差转换为角速度 $\omega$，再通过PID控制生成轮速指令。您的代码隐含了这种转换（例如 `angular` 可能来自偏差计算）。[^2] - **硬件实现**：引用[3] 的舵轮驱动器（如CNS-BL30HB）直接集成角度和速度闭环控制，代码输出的 `front_wheel_angle` 和 `front_wheel_vel` 可直接发送给此类驱动器。[^3] #### 4. 建议与注意事项 - **代码修正**：原始代码中 `SIN(CombinedVelY)` 应为 `SIN(fBodyTheta)`，否则会引入错误。 - **性能优化**：若使用PID控制（引用[2]），可在 `angular` 计算中加入比例项（如 $P \times \text{偏差}$）。 - **实时性**：在高速AGV中，建议采用增量式编码器或霍尔传感器（引用[3]）反馈实际轮速，形成闭环。 ### 相关问题 1. 纯跟踪算法中预瞄距离 $L_d$ 如何自适应调整以提高路径跟踪精度？[^1][^4] 2. 差速轮AGV与舵轮AGV在速度和角度计算上有哪些本质区别？[^1][^3] 3. 如何设计PID控制器参数（如比例增益 $K_p$ ）来优化舵轮AGV的转向响应？[^2] 4. 舵轮驱动器（如CNS-BL30HB）在硬件层面如何实现速度和角度的闭环控制？[^3]
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值