上手机器学习系列-第3篇（下）-聊聊logistic回归

书接上回

在之前的上、中篇，我们分别聊了logistic回归的基本思想、sklearn中的实验方法，本篇中我们一起读一下sklearn中logistic的源代码，一窥其究竟，进一步加深我们对该方法的理解。

代码地址

Github中sklearn的地址为：https://github.com/scikit-learn/scikit-learn，在下属子录中，依次去找sklearn -> linear_model -> _logistic.py, 就能找到我们想看的代码了。

看的过程中，建议结合sklearn官方文档来进行理解。

Logistic回归源代码

本小节我们结合一个实际使用案例来探索源代码的调用逻辑。

我们先梳理一下sklearn调用的固定套路：

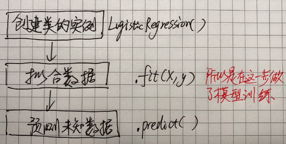
起点

回顾上节我们建立一个logistic回归模型时的执行命令：

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0)

所以这里首先是创建了一个类LogisticRegression的实例，这也是我们正式引用该模型的起点。所以我们先去源代码中找该类的定义。

在其源码文件中，我们看到了两个相似的类定义，一个叫

class LogisticRegression(BaseEstimator, LinearClassifierMixin,SparseCoefMixin)

另一个叫

class LogisticRegressionCV(LogisticRegression, BaseEstimator, LinearClassifierMixin):

从名字也可以看出LogisticRegressionCV一定是增加了交叉验证（Cross Validation）功能的版本。我们先来搞懂基础版本是怎么做的。

拟合数据

创建了LogisticRegression的实例之后，我们就去拟合数据了，回忆一下具体的做法是：

clf = clf.fit(X_train, Y_train)

所以接下来就要去看fit是怎么定义的。原代码比较长，我们不复制了，逐段来走读一下。

最好是带着问题来读，找我们重点关注的部分，否则容易陷入细节中。fit了数据，到底是怎么fit的，根据logistic回归的算法原理， 我们猜想是把特征数据X代入某个线性方程，然后定义一个损失函数，再来求解该损失函数，得到让其最小化/或者最大化的参数。那么就需要去fit中找这个求解损失函数的地方。

看的过程中， 我们就会发现，原来这跟使用的参数solver有关系啊！从LogisticRegression使用文档上的介绍能更清楚地了解solver有哪些可选项：

solver{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default=’lbfgs’
Algorithm to use in the optimization problem.

For small datasets, ‘liblinear’ is a good choice, whereas ‘sag’ and ‘saga’ are faster for large ones.

For multiclass problems, only ‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ handle multinomial loss; ‘liblinear’ is limited to one-versus-rest schemes.

‘newton-cg’, ‘lbfgs’, ‘sag’ and ‘saga’ handle L2 or no penalty

‘liblinear’ and ‘saga’ also handle L1 penalty

‘saga’ also supports ‘elasticnet’ penalty

‘liblinear’ does not support setting penalty='none'

Note that ‘sag’ and ‘saga’ fast convergence is only guaranteed on features with approximately the same scale. You can preprocess the data with a scaler from sklearn.preprocessing.

New in version 0.17: Stochastic Average Gradient descent solver.

New in version 0.19: SAGA solver.

Changed in version 0.22: The default solver changed from ‘liblinear’ to ‘lbfgs’ in 0.22.

从以上内容中，我们可看出来每个solver求解方法适用于什么样的场景，并与哪一种惩罚项比较搭配。以后在创建LogisticRegression时，我们就可以自己指定更多自定义的参数了。而且从源代码中，作者还贴心地给出了每种优化方法的参考文献来源（1217行~1236行），看看人家的代码注释，真是信息量丰富啊。

当solver为liblinear时，我们看到这样一段：

这里就直接return self了，所以如果是liblinear求解方法，这里调用了_fit_liblinear 去求解self.coef_, self.intercept_, n_iter_。如果你继续去挖这个方法的实现，可以发现它来自于用CPython写的一个求解方法，这里我们暂不展开了。

当solver为其它时， 我们看到了这样一段：

sag代表Stochastic Average Gradient，saga是其改进版本。不纠结细节的话，我们猜想这里定义的max_squared_sum是打算要输入给某一个损失函数。
往下找的时候，发现在下面这一段使用上了：

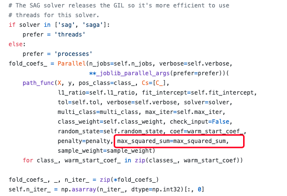
而这里的path_func又是通过下面的命令定义的：

path_func = delayed(_logistic_regression_path)

上面出现的Parallel，delayed 都是python并行编程中的一种技巧，与本算法无关，我们有选择性忽视这些信息，继续找线索。delayed里面的传入参数_logistic_regression_path 的定义中，我们看到：

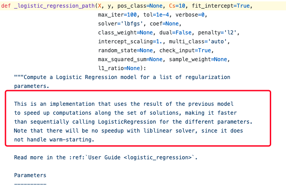
所以这个函数里面就实现sag、saga这两个solver的求解方法，且利用了并行编程，所以实现了更快的速度。这也呼应了我们在上面看到过的一句对不同solver的解释时提到sag、saga对于大规模数据集更快速：

如果继续找，会发现最终是使用了下面这样一段来求解：

感兴趣的同学可以继续去看这个方法的实现，它是在另一个文件中实现的方法，这里只是直接调用了。可见现实世界中，大的软件包就是一块一块的砖头垒起来的，有着一层一层的依赖关系。

回到主线上，继续往下读源码。

这里定义的classes_、n_classes 都是为了用于下面的并行计算。这里至于为啥当n_classes = 2时，要人为改为1，笔者的理解是二分类时，其实我们只需要去预测class = 1 的那一个类，剩下的自然就是另一类了。而多分类时，是one - vs -others， 针对每一个类都要做一次求解。_

带CV的版本

我们再来看看LogisticRegressionCV定义的有哪些不同之处。在实际使用时，该类的实例创建方法为：

clf = LogisticRegressionCV(cv=5, random_state=0).fit(X, y) 

可见这里核心是理解这个cv的参数怎么使用。
我们关注的第一点不同是folds = list(cv.split(X, y))，根据我们对交叉验证方法原理的理解，这里是把数据集均拆了若干份，然后肯定是逐一拿出一份做为验证集。所以要去找它是怎么循环使用这些拆分的数据。

往下找，果然找到一个for循环，也是用到了上文已经提到的那个并行计算方法中。

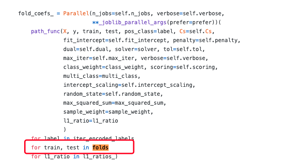
针对交叉验证，对于参数的最终求解又是怎么在多个fold的结果上进行综合呢？

其它的内容，主体逻辑就与不带KV版本的相似了。

结语

本篇啰啰嗦嗦讲了这么多，其实是希望与读者一起通读一篇sklearn中对于logistic回归的实现过程，虽然其中可能仍有一些细节我们并不清楚其底层是怎样实现的，但相比于仅调用一个类的接口，相信我们对于该方法已经有了更深入的了解。也顺便复习了算法本身的一些设计。

至此，我们就完成了上、中、下三篇对于logistic回归的分享，其中并未面面俱到，而是有选择地对一些知识点进行了思考。希望读到这些文章的朋友能有所裨益。

欢迎关注公众号