学习笔记 Day 16 (数据结构算法 -- 1)

算法的五大特征:

1 输入:具有0个或者多个输入

2 输出:算法至少有1个或者多个输出

3 有穷性:在有限的步骤之后会自动结束而不会无限循环,而且每一个步骤可以在接受的时间内完成

4 确定性:算法中的每一步都有确定的含义,不会出现二义性

5 可行性:算法中每一步都是可行的,每一步都能执行有限的次数完成

第一个题目:

代码如下:

lists = []
for a in range(1,1001):
    for b in range(1,1001):
        c = 1000 - b - a
        if a**2 + b**2 = c**2:
            print((a,b,c))
            lists.append((a,b,c))
print(len(lists))

时间复杂度:

描述算法时间上面的效率问题的,用每个程序经过多少个基本运算来衡量

大o表示法:

复杂度形成的函数的近似函数称为这个时间复杂度的大o表示法.

最坏时间复杂度:

算法工作最多完成多少基本操作,即最坏时间复杂度.主要关注的是最坏时间复杂度

时间复杂度,基本计算规则:

1 基本操作,只有常数项,为1

2 顺序结构,按加法计算

3 循环结构,按乘法

4分支结构,取最大值,(两个分支,取复杂度最大的那个)

5 判断算法效率时,只需要关注操作数量的最高此项,其它次要项可忽略

6 没有特殊说明时,我们都是用 最坏时间复杂度

常见时间复杂度:

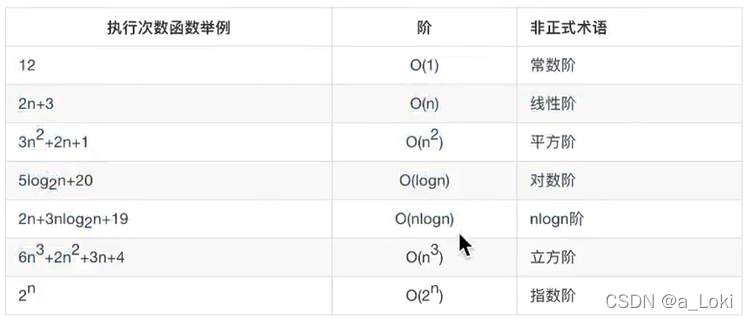
消耗时间从大到小:

 代码时间测量模块timeit:

列表类型不同操作的时间效率:

import timeit
from timeit import Timer

def t1():
    li = []
    for i in range(10000):
        li.append(i)

def t2():
    li = []
    for i in range(10000):
        li += [i]

def t3():
    li = [i for i in range(10000)]

def t4():
    li = list(range(10000))

# 计算每一个列表创建的时间

timeit1 = Timer('t1()','from __main__ import t1') # 最后时间的计算是在外部完成,所以需要从main中调用t1

timeit2 = Timer('t2()','from __main__ import t2')

timeit3 = Timer('t3()','from __main__ import t3')

timeit4 = Timer('t4()','from __main__ import t4')

print('append:',timeit1.timeit(1000)) # .timeit(1000) 计算多少次复杂度
print('+:',timeit2.timeit(1000))
print('列表推导式:',timeit3.timeit(1000))
print('range:',timeit4.timeit(1000))

结果如下:

 列表内置操作的时间复杂度:

 字典内置操作的时间复杂度:

 数据结构:

数据结构就是对数据基本类型的一次封装.

程序 = 算法 + 数据结构

总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体

抽象数据类型:

把数据类型和数据类型运算捆绑在一起进行封装.