用MATLAB设计FIR滤波器

滤波器

滤波器定义

“滤波器(filter),是一种用来消除干扰杂讯的器件,将输入或输出经过过滤而得到纯净的直流电。对特定频率的频点或该频点以外的频率进行有效滤除的电路,就是滤波器,其功能就是得到一个特定频率或消除一个特定频率。”

滤波器种类

滤波器按照频率来分类，可分为高通、低通、带通、带阻以及全通滤波器，根据所需选择合适滤波器。

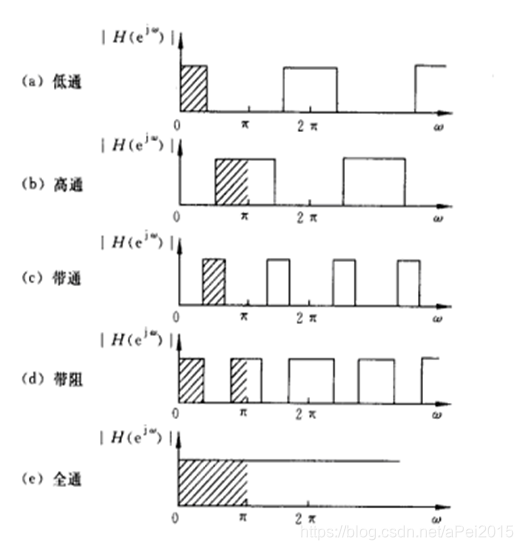
滤波器设计

滤波器的设计方法可分为两大类，一类是IIR，另一类是FIR。对于FIR的设计，一般可以采用等波纹以及窗的方法。

滤波器设计要求

采样频率50khz，带通滤波器，通带15KHz，阻带20KHz，阻带衰减50dB，用凯撒窗设计带通滤波器。

Matlab程序设计滤波器

首先在Matlab中设置所需参数：

fs = 50000;
T = 1/fs;
L = 4000;
t = (0:L-1)*T;

然后从r32文件中读取信号数据：

filename=['文件路径'];
fid=fopen(filename,'r');
Na=4000;
dat=fread(fid,[32,Na],'float');
data=dat(1,:); %data即为所导入信号

绘制信号时域图：

plot(t,data)

得到：

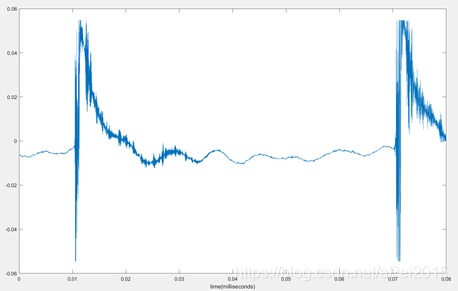
再对其进行FFT：

NFFT = 2^nextpow2(L);
Y = fft(data,NFFT)/L;
f=fs/2*linspace(0,1,NFFT/2+1);
figure
plot(f,2*abs(Y(1:NFFT/2+1)))
title('Single-sided Amplitude Spectrum of y(t)')
xlabel('Frequency(Hz)')
ylabel('|Y(f)|')

得到：

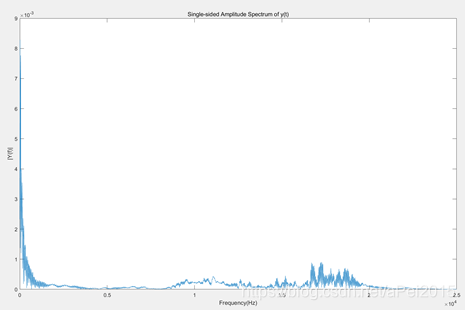
设计滤波器：

fs = 50000;
f = [13000 15000 20000 22000];
dev = [0.01 0.02 0.01];
a = [0 1 0];
[n,wn,beta,ftype] = kaiserord(f,a,dev,fs);
b = fir1(n,wn,'bandpass');
freqz(b)

得到滤波器的幅值相位图：

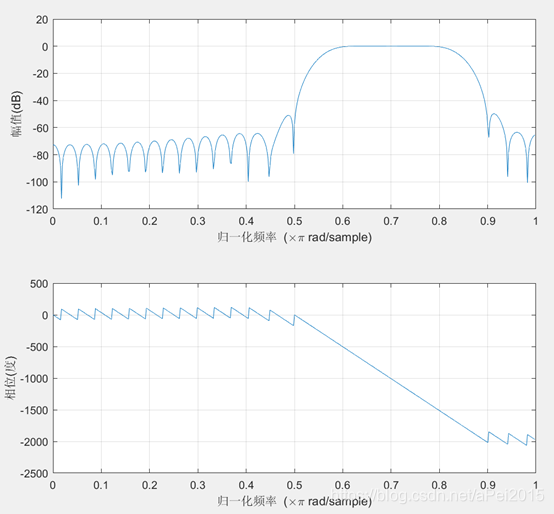
所设计滤波器的分子系数存于b中，使所给信号通过所设计的滤波器，所用程序如下：

d=filter(b,1,data);
plot(t,d)

得到滤波后的信号时域图：

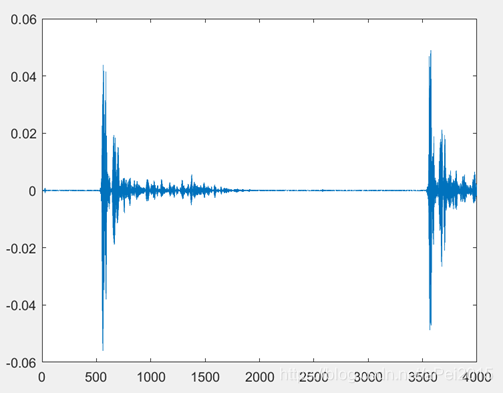
对其进行FFT：

Y _af= fft(d,NFFT)/L;
f_af=fs/2*linspace(0,1,NFFT/2+1);
figure
plot(f_af,2*abs(Y_af(1:NFFT/2+1)))
xlabel('Frequency(Hz)')

得到：

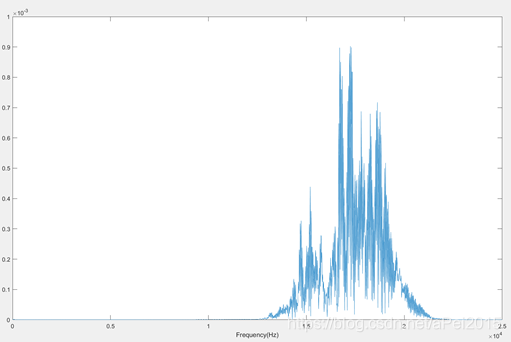
利用Matlab工具箱设计滤波器

另外，还有一种更加快捷的设计方法，即使用Matlab自带的工具箱filterDesigner来设计滤波器：
在Matlab的命令行窗口中输入filterDesigner，得到如下窗口：

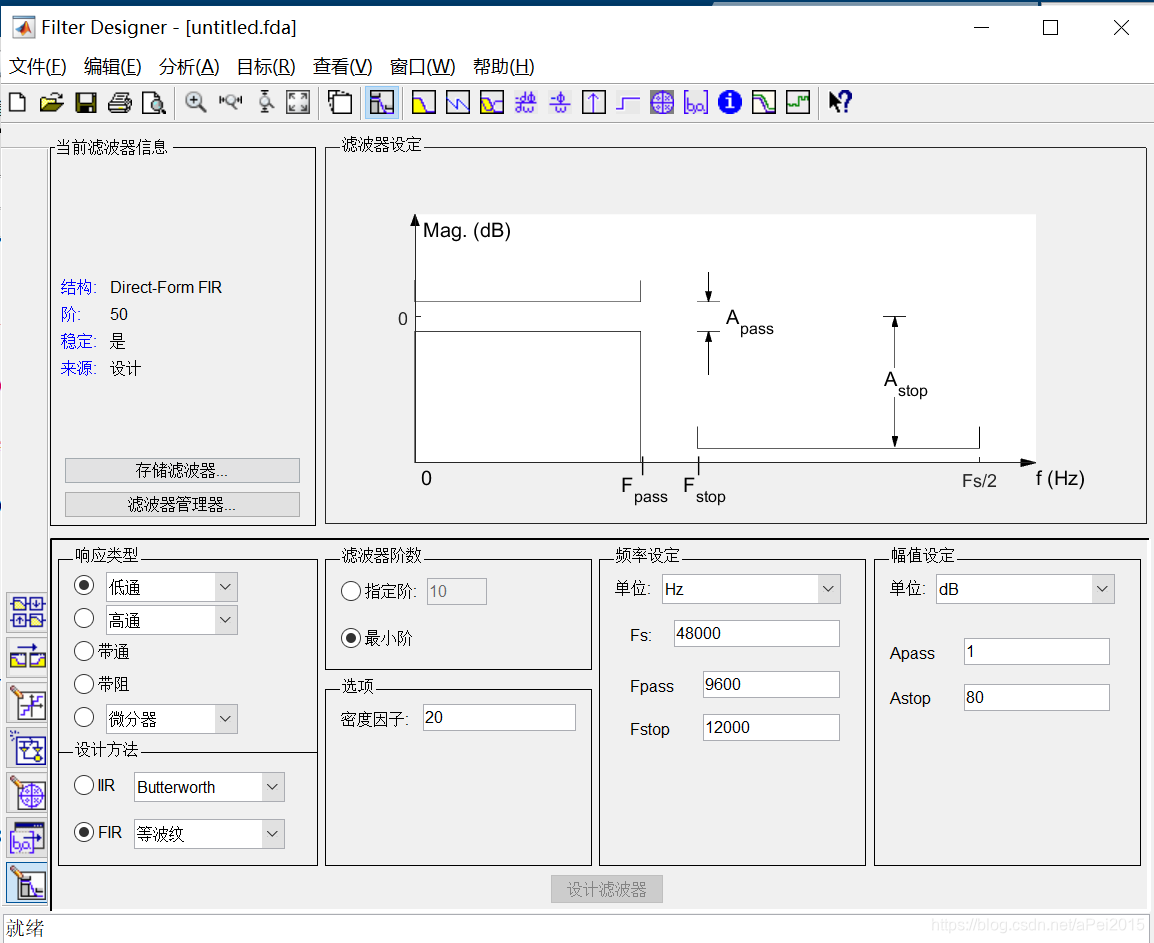
通过选择设置，可以得到滤波器的系数，以本题为例：

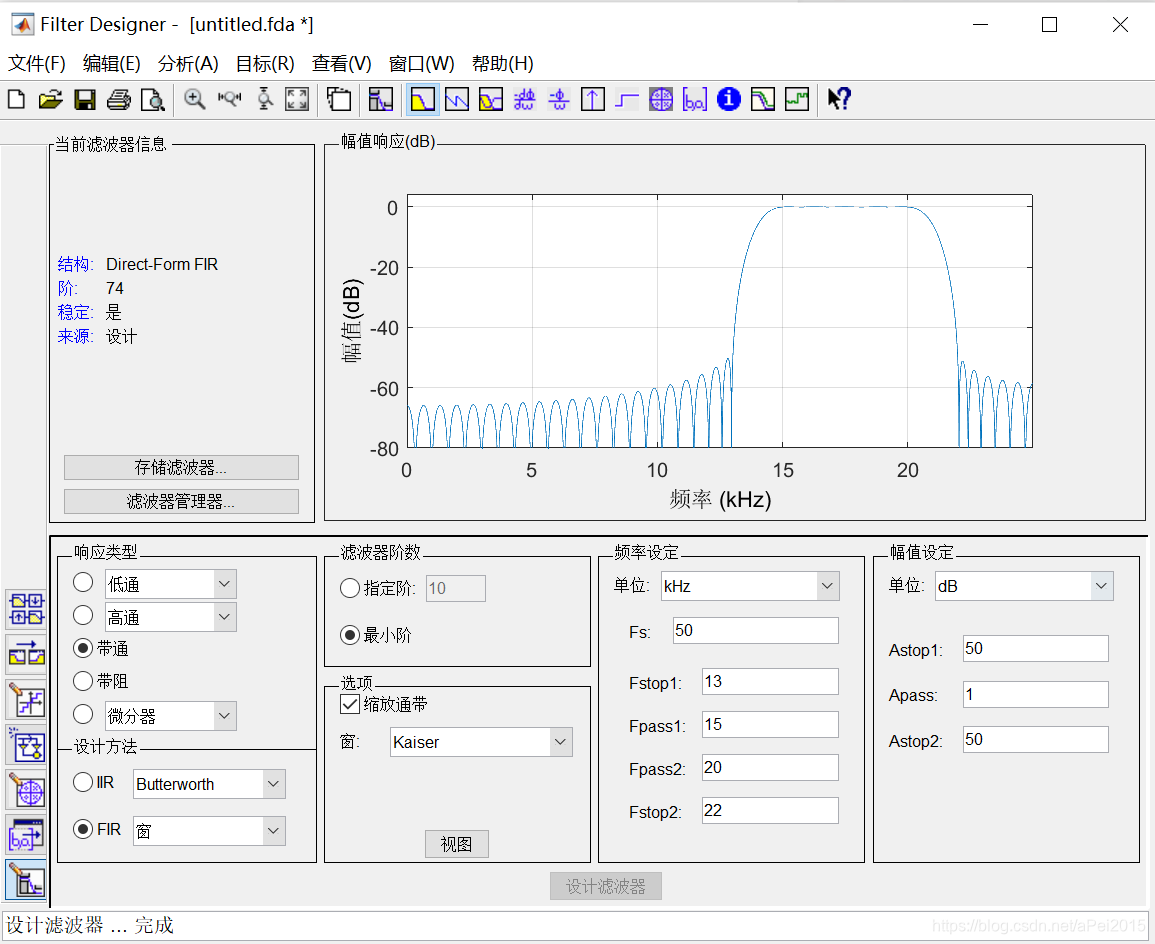
其系数如下：

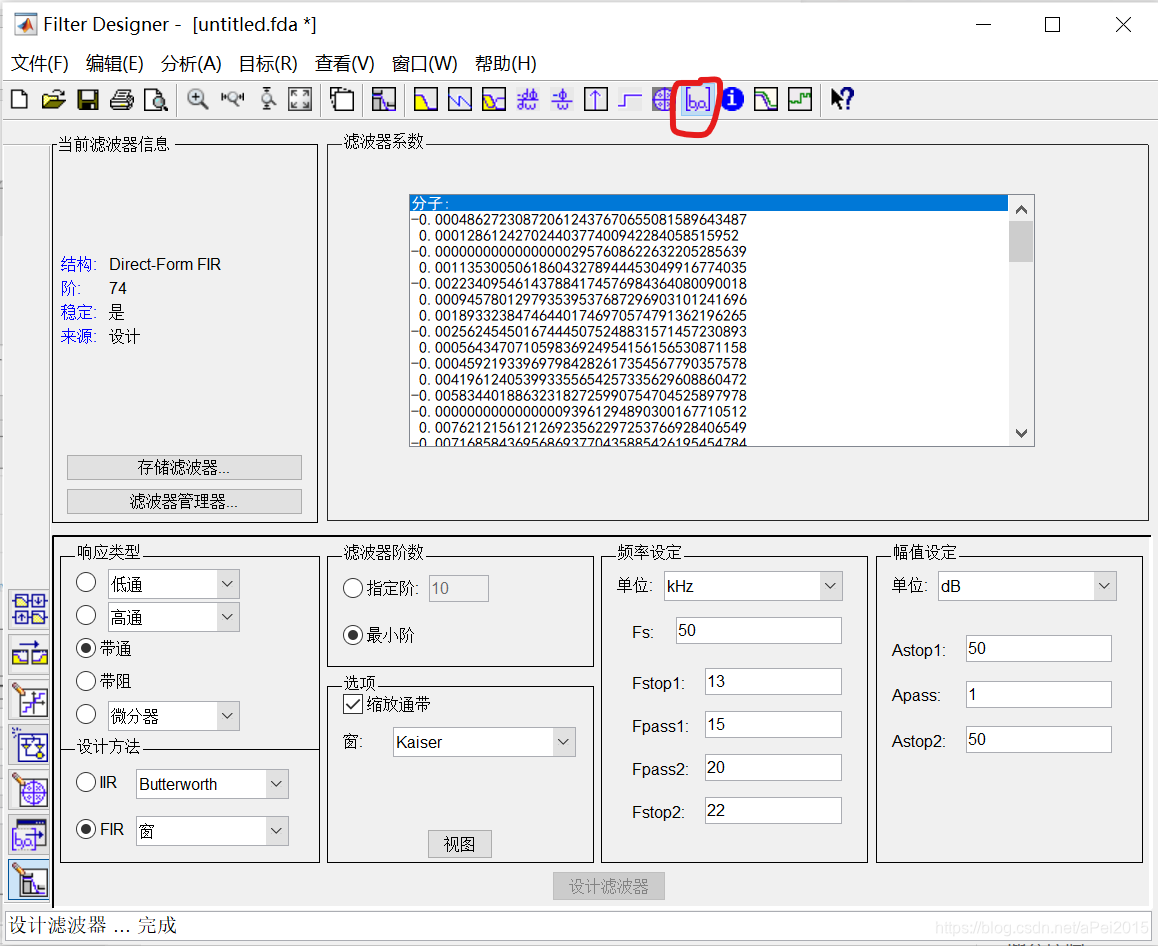
可对其到处头文件，进行数据处理。

总结

本人对于数字信号处理这门课的学习比较冲忙，对于很多知识点都是比较模糊，希望在后续所需时能够进一步的加深理解。
在FIR滤波器设计的过程中，遇到一个比较困惑的点是，根据其他的案例，滤波器系数是包含分子系数以及分母系数，但本例产生的滤波器仅含分母系数，比较困惑，请大佬们指教！