机器学习5---支持向量机

原创

于 2018-09-10 10:14:01 发布 · 519 阅读

·

1

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

本文介绍了支持向量机（SVM）的基础知识，包括线性可分SVM的概念，如何寻找最优超平面以最大化间隔，以及如何通过拉格朗日乘数法和对偶问题求解SVM模型。此外，还讨论了在原始空间无法划分时如何利用核函数将数据映射到高维空间，以解决线性不可分问题，常见的核函数类型也进行了说明。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 线性可分的支持向量机

1.1 支持向量机（SVM）基本型

对于给定的在样本空间中线性可分的训练集，我们有多重办法对其进行划分，以二分类问题为例，如图：

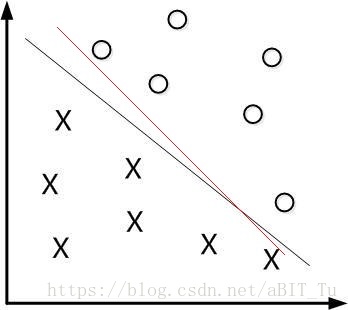
红线和黑线（超平面）都能将两类样本很好的划分开，但是当新样本进入时，黑线比红线更加有可能正确划分新的样本，换句话说：越位于两类样本“中心”的划分超平面越能够容忍样本的局部扰动，其的泛化能力越好。

基于以上思想，我们准备求解最优超平面。

首先，记超平面的线性方程为 $w^{T}x+b=0$ ，其中 $w$ 为法向量。根据点到直线的距离公式，得到样本空间任一点x超平面的距离可以写成 $r=\frac{|w^{T}x+b|}{||w||}$ 。

接着，为了方便计算，我们将两类样本使用正类和负类表示，即若 $y_{i}=+1$ ，则 $w^{T}x_{i}+b\geqslant +1$ ;若 $y_{i}=-1$ ，则 $w^{T}x_{i}+b\leqslant -1$ ，能够使得等号成立的样本向量称之为“支持向量”，因为它们是离超平面最近的训练样本，它们确定了两个类别之间的“间隔”。

然后，找到最优超平面也就转换成寻找“最大间隔”问题，即

$\underset{w,b}{max} \frac{2}{||w||}$ (

最低0.47元/天解锁文章

200万优质内容无限畅学

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。