HDU6038-Function（置换群）

Function

                                                                      Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
                                                                                                Total Submission(s): 934    Accepted Submission(s): 420

Problem Description

You are given a permutation  a  from  0  to  n−1  and a permutation  b  from  0  to  m−1 .

Define that the domain of function  f  is the set of integers from  0  to  n−1 , and the range of it is the set of integers from  0  to  m−1 .

Please calculate the quantity of different functions  f  satisfying that  f(i)=bf(ai)  for each  i  from  0  to  n−1 .

Two functions are different if and only if there exists at least one integer from  0  to  n−1  mapped into different integers in these two functions.

The answer may be too large, so please output it in modulo  109+7 .

 

Input

The input contains multiple test cases.

For each case:

The first line contains two numbers  n,   m .  (1≤n≤100000,1≤m≤100000)

The second line contains  n  numbers, ranged from  0  to  n−1 , the  i -th number of which represents  ai−1 .

The third line contains  m  numbers, ranged from  0  to  m−1 , the  i -th number of which represents  bi−1 .

It is guaranteed that  ∑n≤106,   ∑m≤106 .

 

Output

For each test case, output " Case # x :  y " in one line (without quotes), where  x  indicates the case number starting from  1  and  y  denotes the answer of corresponding case.

 

Sample Input

  

   3 2
1 0 2
0 1
3 4
2 0 1
0 2 3 1
  

 

Sample Output

  

   Case #1: 4
Case #2: 4
  

 

Source

2017 Multi-University Training Contest - Team 1

 

题意：给两个数列a（元素个数为n）和b（元素个数为m），求满足f(i) = b[f(a[i])] 的组合情况有多少种

题解：由第二个样例：

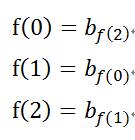
对于这组数来说，假如我们先指定了f（0）对应的在b中的值，那么根据第2个式子，就可以得出f（1），根据f（1）就又可以得出f（2），最后根据f（2）就可以检验f（0）的值是否正确。

这也就是说，对于a中的一个循环节，只要确定了其中一个数所映射的值，那么其它数就都被相应的确定了。

所以需要先计算出a和b中的循环节个数和每个循环节对应的个数，然后根据循环节的约数关系就可以判断是否成立

答案就是：当b中的循环节的长度是a的循环节长度的约数的时候，a循环节可以指定数字的个数是b的循环节长度

这里有一个规律就是：0~n 的排列，是一定存在循环节的，而且多个循环节是不会有交叉的，所以最后的结果应该相乘

#include <iostream>  
#include <cstdio>  
#include <cstring>  
#include <string>  
#include <algorithm>  
#include <map>  
#include <cmath>  
#include <set>  
#include <stack>  
#include <queue>  
#include <vector>  
#include <bitset>  
#include <functional>  
using namespace std;
#define LL long long  
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;

int n, m;
int a[1000009], b[1000009];
int xa[1000009], xb[1000009];

struct node
{
	int x, sum;
}x[1000009], y[1000009];

LL mpow(LL x, LL y, LL p)
{
	LL ans = 1;
	while (y)
	{
		if (y & 1) ans = (ans * x) % p;
		x = (x * x) % p;
		y >>= 1;
	}
	return ans;
}

int main()
{
	int cas = 0;
	while (~scanf("%d %d", &n, &m))
	{
		for (int i = 0; i < n; i++) scanf("%d", &a[i]);
		for (int i = 0; i < m; i++) scanf("%d", &b[i]);
		int cnt1 = 0, cnt2 = 0;
		for (int i = 0; i < n; i++)
		{
			if (a[i] == -1) continue;
			int cnt = 0;
			if (a[i] != -1)
			{
				int k = a[i];
				while (a[k] != -1)
				{
					cnt++;
					int kk = k;
					k = a[k];
					a[kk] = -1;
				}
			}
			xa[cnt1++] = cnt;
		}
		for (int i = 0; i < m; i++)
		{
			if (b[i] == -1) continue;
			int cnt = 0;
			if (b[i] != -1)
			{
				int k = b[i];
				while (b[k] != -1)
				{
					cnt++;
					int kk = k;
					k = b[k];
					b[kk] = -1;
				}
			}
			xb[cnt2++] = cnt;
		}
		sort(xa, xa + cnt1);
		sort(xb, xb + cnt2);
		int tot1 = -1,tot2=-1;
		for (int i = 0; i<cnt1; i++)
		{
			if (i == 0 || xa[i] != xa[i - 1]) x[++tot1].x = xa[i], x[tot1].sum = 1;
			else x[tot1].sum++;
		}
		for (int i = 0; i<cnt2; i++)
		{
			if (i == 0 || xb[i] != xb[i - 1]) y[++tot2].x = xb[i], y[tot2].sum = 1;
			else y[tot2].sum++;
		}
		LL ans = 1;
		for (int i = 0; i <= tot1; i++)
		{
			LL sum = 0;
			for (int j = 0; j <= tot2&&x[i].x>=y[j].x; j++)
				if (x[i].x % y[j].x == 0) sum = (sum + 1LL * y[j].x * y[j].sum) % mod;
			ans = (ans * mpow(sum, x[i].sum, mod)) % mod;
		}
		printf("Case #%d: %lld\n", ++cas, ans);
	}
	return 0;
}