神经网络基础介绍（一）

        今天我们来介绍神经网络的一些基础知识，例如传递函数，学习率，递归函数等一些的基础知识，本文章是参考b站的教学视频。

       我们以吃豆人为例子，顾名思义，吃豆人以豆子为食，但是在一个环境下，豆豆的毒性和大小相关，如果吃了毒性过大的豆子，吃豆人就会受伤。目前，该环境的豆豆的毒性和大小关系如下。

        目前，我们很容易看出豆豆的毒性和大小关系是一个过原点的一次 函数，但是呢，吃豆人并不知道这层关系，它只会吃一个豆子，对豆子大小和毒性的关系进行修改。假设吃豆人对豆豆的关系认知如下：

        看出来，这关系认识的非常差， 有一种方法就是吃完豆豆根据豆豆的毒性来调节一次函数斜率的大小，使其符合现实。调节方法该如何实现呢，首先让我们引用误差e，e用来描述吃豆人认为豆豆毒性和实际毒性的误差，这里为实际豆豆毒性-预测豆豆毒性，我们得用误差来调节一次函数的斜率。如果误差为正数，我们就提高斜率，误差为负数我们就降低斜率。接下来我们就要应用一个新的要素，就是学习率alpha，这个就是控制我们调节斜率的速度。学习率越大，调节的速度就越快，但是可能会在正确解附近产生震荡。斜率调节方式为：

        

        可能有人发现我又多乘了一个x，这是之前只考虑了x为正的情况，当x为负的时候调节方法与x为正的时候相反，大家可以自己证明。python代码如下：

import dataset
import matplotlib.pyplot as plt

x, y = dataset.get_beans(100)

plt.title("Size-Toxicity Function", fontsize=12)
plt.xlabel("beans size")
plt.ylabel("Toxicity")

w = 0.5

for m in range(100):
    for i in range(100):
        x1 = x[i]
        y1 = y[i]
        y_pre = w*x1
        e = y[i] - y_pre
        alpha = 0.01
        w = w + alpha*e*x

print(w)
y_pre = w*x

plt.plot(x, y_pre)
plt.scatter(x, y)
plt.show()

        这里我们就得到了一个比较符合豆豆大小和毒性的关系图。但是我们发现用实际豆豆毒性-预测豆豆毒性来表示误差可能会出现问题，这里我们用和来表示预测豆豆的毒性和实际毒性。

   

   

        通过展开误差e我们发现了e是关于k的一元二次函数，且是一个开口向上的抛物线，且在顶点处，e最小。图像如下：

         这里只是一个豆豆的结果，如果将所有豆豆关于e和w的一元二次函数相加的话其结果也依然是一个一元二次函数。将所有的误差相加再除以样本的个数，我们就得到了均方误差：

        

   

   

        上面的函数称为代价函数，因为其本身还是一个一元二次方程，我们可以利用一元二次方程求中线的方法快速得到最低点的坐标，，这个也称为正规方程。

import dataset
import matplotlib.pyplot as plt
import numpy as np

xs, ys = dataset.get_beans(100)

w = 0.1
y_pre = xs*w

es = (ys - y_pre)**2 #numpy里的数组计算是每个元素进行原算，数组的大小不变

sum_e = np.sum(es)/100

print(sum_e)

ws = np.arange(0, 3, 0.1)

es = []
for w in ws:
    y_pre = w*xs
    e = np.sum((ys - y_pre)**2)/100
    es.append(e)

plt.title("Cost Function", fontsize=12)
plt.xlabel("w")
plt.ylabel("e")
plt.plot(ws, es)
plt.show()

w_min = np.sum(xs*ys)/np.sum(xs*xs)
print("e最小点w："+str(w_min))

y_pre = xs*w_min
plt.plot(xs, y_pre)
plt.scatter(xs, ys)

plt.show()

 

        以上就是python里的代码了。但是这个方法只适用于较小的数据量，因为其一次性就计算出了所有的数据，当数据量变大时就需要更大的存储空间和算力了。接下来我们看代价函数的图像：

 

        这里我们将预测函数的斜率设为w，将代价函数的斜率设置为k，通过图像我们可以发现，我们可以通过一元二次函数的斜率来判断目前的斜率和准确斜率之间的关系，当某点的斜率为正时，说明该点对应的w在准确值的右边，且斜率越小，距离准确值就越近。因此，我们可以通过斜率来控制w的大小。某一点所对应的斜率的大小如下：

        

        

        得到斜率后，我们就可以通过斜率来控制w的大小了，这里我们还是会用到学习率alpha，调节方式为：

        

        

        这个方法就是梯度下降，其python代码如下：

import dataset
import matplotlib.pyplot as plt
import numpy as np

xs, ys = dataset.get_beans(100)

w = 0.1

for i in range(100):
    x = xs[i]
    y = ys[i]
    k = 2*(x**2)*w+(-2*x*y)
    alpha = 0.1
    w = w - alpha*k
    plt.clf()
    y_pre = xs * w
    plt.xlim(0, 1)
    plt.ylim(0, 1.2)
    plt.plot(xs, y_pre)
    plt.scatter(xs, ys)
    plt.pause(0.01)

plt.show()

        

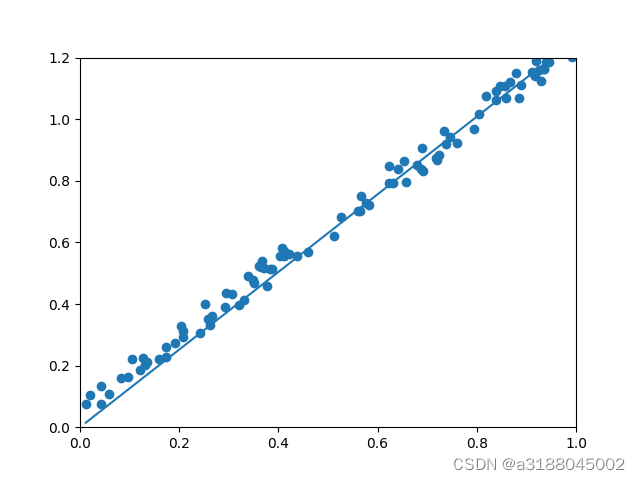
        从代码看，我们是用的是单个样本的来经行梯度下降，虽然会有震荡和波动，但是最后还是会回归到最优解。这种方法为随机梯度下降，如果使用全部的样本进行梯度下降，则称为批量梯度下降，但是如果数据量过大的话就和上面的正规方程差不多麻烦了，如果将两种方法相结合，我们就得到了mini-梯度下降，即每次选择样本中的n个样本作为一批进行梯度下降。

        如果现在的环境发送了变化，及豆豆的毒性和大小的关系不经过原点，其关系图和吃豆人的认知函数如下：

        我们这时候再用上面的方法就没有效果了，或者说效果不好。现在我们要引入了一个截距参数b，这样我们就可以实现预测函数的移动了。

        这时候我们来观察代价函数：

   

   

        这里我们就要用3维图来观察了e和w，b的关系了，我们发现，无论b取何值，e都是关于x的一元二次函数，我们分别取不同的b，就可以得到下图：

        我们可以看出e关于b，w的图像是一个曲面，且有一个最低点，这个点就是我们所要求的w和b。这里我们可以用上面求斜率的方法来进行梯度下降，只不过这里的方法是求梯度。，其方法为：

       

        

       用代价函数来修正w和b的过程就称之为反向传播，梯度的调整方法与上面一样，这里就不详细介绍了。代码如下：

import dataset
import matplotlib.pyplot as plt
import numpy as np

xs, ys = dataset.get_beans(100)

plt.xlim(0, 1)
plt.ylim(0, 1.2)

w = 0.1
b = 0.1

plt.scatter(xs, ys)
plt.show()

for m in range(100):
    for i in range(100):
        x = xs[i]
        y = ys[i]

        dw = 2*x**2*w + 2*x*b - 2*x*y
        db = 2*b + 2*x*w - 2*y
        alpha = 0.01
        w = w - alpha*dw
        b = b - alpha*db
        y_pre = xs * w + b

    plt.clf()
    plt.xlim(0, 1)
    plt.ylim(0, 1.2)
    plt.plot(xs, y_pre)
    plt.scatter(xs, ys)
    plt.pause(0.01)

plt.show()

        上面就是线性规律的预测方法，并且介绍了一些常见的名词，之后会介绍非线性的规律预测。