1~10
10.颜色转换
#include <stdio.h>
double Max(double a,double b,double c){
double max;
max=(a>b)?a:b;
max=(c>max)?c:max;
return max;
}
double Min(double a,double b,double c){
double min;
min=(a<b)?a:b;
min=(c<min)?c:min;
return min;
}
int main()
{
double R,G,B;
double H,S,V;
scanf("%lf%lf%lf",&R,&G,&B);
R/=255,G/=255,B/=255;//很屑的单位转换
V=Max(R,G,B);
double min=Min(R,G,B);
if(V==0)S=0;//分母不为0
else S=(V-min)/V;
double diff=V-min;//额外diff注意设成浮点类型,想象一下如果是int是否会进入循环
//假设此时V,min都小于1
if (V!= min) {
if (V == R) {
H = 60 * ((G - B)/diff);
} else if (V == G) {
H = 60 * (2 + (B - R)/diff);
} else if (V == B) {
H = 60 * (4 + (R - G)/diff);
}
if (H < 0) {
H += 360;
}
}else H=0;
printf("%.4lf,%.4lf%%,%.4lf%%\n", H, S*100, V*100);//注意加了百分号%%
return 0;
}11~20
11.分数的加减乘除
#include<stdio.h>
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
int main()
{
int u1,u2;
int d1,d2;
scanf("%d/%d %d/%d",&u1,&d1,&u2,&d2);
int D=gcd(d1,d2);
int d11=d1/D;
int d21=d2/D;
D=(d1/D)*(d2/D)*D;
int u=u1*d21+u2*d11;
int res1=gcd(u,D);
printf("(%d/%d)+(%d/%d)=%d/%d\n",u1,d1,u2,d2,u/res1,D/res1);
int U=u1*d21-u2*d11;
int res2=gcd(U,D);
printf("(%d/%d)-(%d/%d)=%d/%d\n",u1,d1,u2,d2,U/res2,D/res2);
int d12=d1*d2;
int u12=u1*u2;
int la=gcd(d12,u12);
printf("(%d/%d)*(%d/%d)=%d/%d\n",u1,d1,u2,d2,u12/la,d12/la);
int d22=d1*u2;
int u22=u1*d2;
int si=gcd(d22,u22);
printf("(%d/%d)/(%d/%d)=%d/%d\n",u1,d1,u2,d2,u22/si,d22/si);
}但是目前有两个问题:
1.如果作差出现0的话,辗转相除法用不了,运行会报错
2.也是辗转相除,引入负的公约数,'-'会出现在分母(
但是既然它给的数据是科学合理的,以上
12.幂数模
#include<stdio.h>
int main()
{
unsigned long long a,b,m;//注意到2^63
unsigned long long s=1;
scanf("%llu%llu%llu",&a,&b,&m);
//a%=m;(这是笔者第一次的答案,这次取模很有可能导致s=0)
while(b){
if(b&1){
s*=a;
s%=m;//防止数据爆炸,乘完就取模
}
a*=a;
a%=m;
b>>=1;//同上
}
s%=m;//最后一道防线
printf("%llu\n",s);
return 0;
}13.对称数
#include<stdio.h>
#include<string.h>
int main()
{
char a[50]="\0";//记得初始化
scanf("%s",a);//a就是它的地址了
int j=strlen(a);
int point=0;//便于判断是否出现非对称的数字
for(int i=0;i<=j;i++){
a[i]-='0';
if(a[i]==2||a[i]==3||a[i]==4||a[i]==5||a[i]==7){
printf("No\n");
point=1;
break;
}
}
if(point==0)
printf("Yes\n");
return 0;
}
[点击并拖拽以移动]
15.倍数和
#include<stdio.h>
#include<stdlib.h>//后面要用到malloc
int main()
{
int *a,l;//10^9所以就用int了,不浪费哈
scanf("%d",&l);
a=(int *) malloc (sizeof(int)*l);
for(int i=0;i<l;i++)
scanf("%d",&a[i]);//如果写成scanf("%d\n")反而读不进来,\n会被认为是空格
for(int i=0;i<l;i++){
int sum=0;//每次一个新的n都要初始化哦
for(int k=3;k<a[i];k++){//也可以从1或者2开始,没必要
if(k%3==0||k%5==0)
sum+=k;
}
printf("%d\n",sum);
}
free(a);//借了要还回去哦!
return 0;
}
[点击并拖拽以移动]
16.方阵
#include<stdio.h>
#include<stdlib.h>
int main()
{
int n;
scanf("%d",&n);
int **a=(int **)malloc(sizeof(int*)*n);//行,每一行,都是一个数组
for(int i=0;i<n;i++)
a[i]=(int *)malloc(sizeof(int)*n);//列
for(int i=0;i<n;i++){
a[i][i]=0;
for(int k=i+1;k<n;k++)
a[i][k]=k-i;//横着看,每一位上的数字可以理解为,该点与a[i][i]的距离
for(int j=i-1;j>=0;j--)
a[i][j]=i-j;
}
for(int i=0;i<n;i++){
for(int k=0;k<n;k++){
printf("%d",a[i][k]);
if(k<n-1)
printf(" ");
else printf("\n");//注意格式
}
}
free(a);//注意释放内存
return 0;
}
19.小数转化为分数
#include<stdio.h>
int main()
{ //实际上利用1.2=6/5
//1.2*4!=(int)(1.2*4)而1.2*5==6
double num;
scanf("%lf",&num);
int n=1,k=1;
while(n*num!=(int)(num*n))
n++;
printf("%d/%d",(int)(num*n),n);
return 0;
}21~30
23.阶乘倍数
零零散散卡了两三天....
这里感谢Rwmwdy.学长的思路
- n!会超时
- 原问题关键在于从1到n中尽可能快地找到k的因子,使它们相乘为k(也有可能为k的倍数:如12=2*2*3,此时出现两个2,所以为了引入第二个因子2,我们不得不取4,那么最终的结果就是24=2*k=4!)
- 那么我们需要找到所有的因子吗,实质上,我们只关心最大的因子p,如果一切顺利的话,p!就是我们想要的结果
- 但是问题来了,第一,像2*2*2*3*3=72的情形,最大因子为36,而实际输出为9;第二,一定需要从2遍历到(k-1)吗?
- 为了回答上述问题,我们做这样的思考,对于k=m*q(假设m<q),那么必然有m<=sqrt(k),q>=sqrt(k),m和q总是成对出现,找到了m也就等于找到了q,也就是说我们只需要遍历从2到sqrt(k)
- 按理来讲,只需要找到小于或等于sqrt(k)的最大因子即可
- 但事实上,如果我们进一步削弱k,使得m*q=k/2(2只是为了举例,这里可以是任何小于sqrt(k)的k的因数),那q岂不是更小
- 当然k(这里的k是找到合适的数字便对它取整的结果)此时可能已经小于sqrt(k)并且小于此时正在遍历的数字
- 不过没关系,还记得第二条吗,不断扩大k,知道它第一次超过sqrt(k),便是最小的n(其实这里我也不能严格说明情况)
- 这里模拟一下遍历的情形,假设k为48,那么就需要从2遍历至6(sqrt(48))
-
2 3 4 5 6 ...... 8 48/2=24 24/3=8 8/4=2 2(no change) 2(nochange) 2 2*4(第一次超过6的情形) #include <stdio.h> #include <math.h> int main() { long long k, p = 1; scanf("%lld", &k); long long num = k; for (long long i = 2; i <= sqrt(num); i++) { if (k % i == 0) k /= i; if (k == 1){ p = i; break; } } if (k != 1){ if (k == num) { printf("%lld", num); return 0; } else{ for (long long i = sqrt(num)+1;; i++) //注意从sqrt(num)+1开始 //试想若num为9这样的由两个质数3合成的平方数 //那么i%k==0,p=i=sqrt(num)? { if (i % k == 0){ p = i; break; } } } } printf("%lld", p); return 0; }感谢这位热心市民🦌同学的指正!
27.竖式乘法
#include<stdio.h>
//计位数
int Cnt(int a) {
int cnt_result=0;
while(a) {
a/=10;
cnt_result++;
}
return cnt_result;
}
//乘法 ,右对齐
int Print(int sum,int mylen,int number,int judge) {
for(int i=0; i<sum; i++) {
if(judge==1&&i==0) printf("x");//为了打印'x'出来,不想再写一遍函数了
else if(i<(sum-mylen)) printf(" ");
else {
printf("%d\n",number);
break;//记得打印数字之后会占位,应该打印完break,否则就会反复输出这个数字
}
}
return 0;
}
//分割线
int Print1(int sum) {
for(int i=0; i<sum; i++) {
if(i<sum-1) printf("-");
else printf("-\n");
}
return 0;
}
//下半部分加法 ,每次向左推进一位
int Print3(int sum,int mylen,int number,int cnt) {
for(int i=0; i<sum; i++) {
if(i<(sum-mylen-cnt)) {
if(sum-mylen-cnt==1&&i==0) printf("+");//为了在最后一行输出'+'
else printf(" ");
} else {
printf("%d\n",number);
break;
}
}
return 0;
}
int main() {
int a,b,cnt,cnt_a,cnt_b=0;
int cnt1=0;
scanf("%d%d",&a,&b);
cnt=Cnt(a*b);
cnt++;
cnt_a=Cnt(a);
cnt_b=Cnt(b);
Print(cnt,cnt_a,a,0);
Print(cnt,cnt_b,b,1);
Print1(cnt);
int b1=b;
if(b>9)
//做判断,若是乘以一位数,就不用做后续的加法了咩
{
while(b1) {
int digit=b1%10;
int result=a*digit;
if(result==0){
for(int i=0;i<cnt;i++){
if(i<cnt-cnt1-1){
printf(" ");
}
else{
printf("0\n");
break;
}
}
}
else Print3(cnt,Cnt(result),result,cnt1);
cnt1++;
b1/=10;
}
Print1(cnt);
}
Print(cnt,Cnt(a*b),a*b,0);
return 0;
}
28.毕达哥拉斯三元组
#include<stdio.h>
int main()
{
int n,a,b,c;
scanf("%d",&n);
for(a=0;a<(n-3)/3;a++){
//至于为什么是(n-3)/3
//也是为了让a尽可能地大,但是又比n小,更快
for(b=a+1;b<(n-1)/2;b++){
c=n-a-b;
//注意此处直接假设c满足一组条件,更快
if(a*a+b*b==c*c){
printf("%d",a*b*c);
return 0;
}
}
}
}
29.最大数字
#include <stdio.h>
// 找到最大的不递减数字
// 计位数
// 从最高位开始遍历
// 发现递减,上一位减一,该位为9,其余依次为9
int main()
{
int num, cnt = 0, sum = 1, point = 0, pos;
scanf("%d", &num);
int num1 = num;
while (num1)
{
num1 /= 10;
cnt++;
sum *= 10;
}//为了从高位开始取数,
//目前想到的解释是,更块,
//(从低位取反正也需要一直找到最高位上不满足条件那个
sum /= 10;
int headNumber = num / sum;
num %= sum;
sum /= 10;
//为了取两项作比较,只需要找两个位置
for (int i = 0; i < cnt-1; i++)
{//注意此处是cnt-1.因为cnt-1时已经取到了cnt位
int nowNumber = num / sum;
num %= sum;
sum /= 10;
if (nowNumber < headNumber)
{
headNumber--;
pos = i;
point = 1;
}
printf("%d", headNumber);
headNumber = nowNumber;
if (point == 1) break;
}
if(point==0) printf("%d",headNumber);
if (point == 1)
{
for (int i = pos + 1; i < cnt; i++)
{
printf("9");
}
}
return 0;
}
30.好数字
#include<stdio.h>
#define Mod 1000000007
//巩固一下宏定义吧
int main()
{
unsigned long long n,sum=1;
scanf("%llu",&n);
for(unsigned long long i=0;i<n;i++){
if(i%2==0) sum=(sum*5)%Mod;
else sum=(sum*4)%Mod;
//乌鱼,这是抄的答案,好吧,确实也不会溢出
}
printf("%llu",sum);
return 0;
}31~40
31.哈萨德数
#include<stdio.h>
int Har(int n){
int t=n,s=0;
while(t){
s=s+t%10;
//这是好的写法,不会改变t的值
t/=10;
}
if(s&&n%s==0) return n/s;
return 0;
}
int main()
{
int n,cnt=0;
scanf("%d",&n);
while(Har(n)){
n=Har(n);
cnt++;
if(n==1) break;//大家可以自行代入一下n=1的情况
}
printf("%d",cnt);
return 0;
}32.运动会
在这道题之前我们需要了解一下
解题思路以及你可能不了解的欧拉函数
#include <stdio.h>
//欧拉函数
int euler(int n){
int res=n;
int a=n;
//其实笔者也不清楚,为什么用a替换n之后就ac了,
//不过ai说尽量不要改变传入的n的值(可是n也没传地址来啊?疑惑...
for(int i=2;i*i<=a;i++){
if(a%i==0){
res=res/i*(i-1);
while(a%i==0){
a/=i;
}
}
}
if(a>1) res=res/a*(a-1);
//这个表达式实际上就是--a,可是--a 就行不通
return res;
}
//计算从2到n-1的欧拉函数值之和
//为什么是n-1呢,因为我们以观察者为(0,0)建立坐标系
//所以6*6的方阵边界是n-1=5
long long add_euler(int n){
long long sum=0;
for(int i=2;i<n;i++){
sum+=euler(i);
//个人感觉这里不是很需要数组来储存每个i对应的欧拉值
}
return sum;
}
int main() {
int n;
scanf("%d",&n);
if(n==1){
printf("0");
return 0;
//特殊判断1
}
else printf("%lld",add_euler(n)*2+3);
//(1,0)(0,1)(1,1)在上述讨论中并未涉及,所以加3
//坐标可以交换位置如(4,5)(5,4),所以乘2
return 0;
}
33.基思数
#include <stdio.h>
#include<stdlib.h>
#include<math.h>
//计位数为cnt
//前cnt项之和为cnt+1项
//判断每一项与n是否相等
//判断每一项是否大于n,是的话就停止
//计位数,一是为数组申请内存,二是为了从最高位取数字
int Cnt(int n){
int cnt=0;
while(n){
n/=10;
cnt++;
}
return cnt;
}
int IsKeith(int num){
int cnt=Cnt(num),sum=0;
int num1=num;
int s=pow(10,cnt-1);
//为了从最高位取数字,视觉上的从前往后吧...
int *store=(int *)malloc(sizeof(int)*(cnt+1));
//这里取cnt+1大小的数组
for(int i=0;i<cnt+1;i++){
if(i==cnt) store[i]=sum;
else{
store[i]=num1/s;
num1%=s;
s/=10;
sum+=store[i];
}
}
if(store[cnt]==num) return 1;
else{
while(store[cnt]<num){
sum=0;
for(int i=0;i<cnt+1;i++){
if(i!=cnt){
store[i]=store[i+1];
sum+=store[i];
}
else store[i]=sum;
}
}
if(store[cnt]==num){
free(store);
//记得释放内存
return 1;
}
else{
free(store);
return 0;
}
}
}
int main()
{
int num;
scanf("%d",&num);
int flag=IsKeith(num);
if(flag==1) printf("Yes");
else printf("No");
return 0;
}37.可变参数累加
#include<stdio.h>
#include<stdarg.h>
int sum(int num,...){
va_list args;
//声明使用列表
int total=num;
va_start(args,num);
//初始化列表即va_start(name,theFirstNumber)
for(int i=0;;i++){
int val=va_arg(args,int);
//读取输入文件va_arg(name,theTypeOfListMember)
//值得注意的是,这里使用一次va_arg函数,就会读入一个成员
//笔者第一次的写法是if(va_arg(args,int)==0) break;
total+=val;
if(val==0) break;
}
va_end(args);
//释放
return total;
}
int main()
{
int a,b,c,d,e,f;
scanf("%d%d%d%d%d%d",&a,&b,&c,&d,&e,&f);
int res=sum(a,b,0)-sum(c,d,e,f,0);
printf("%d",res);
return 0;
}38.光线追踪
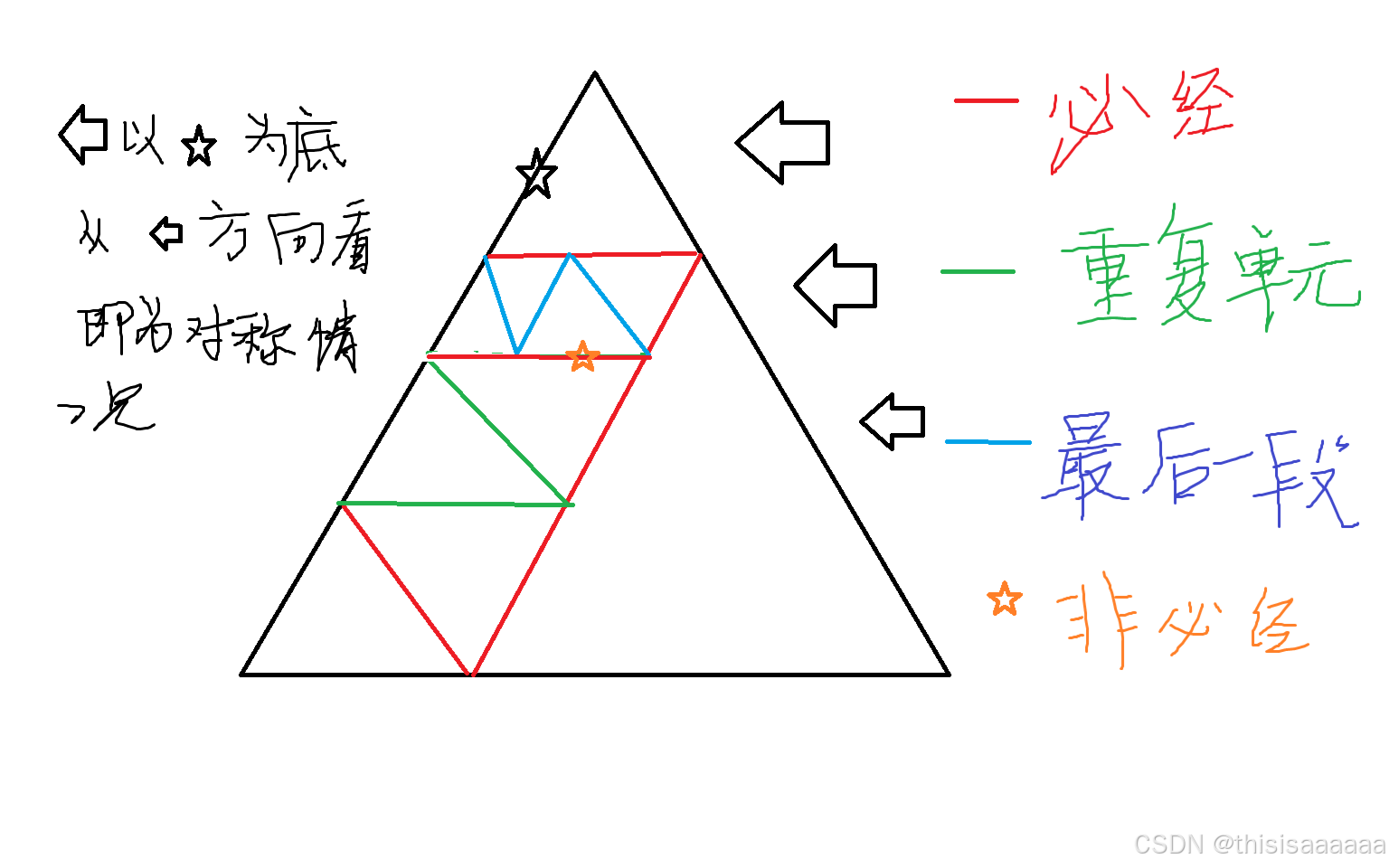
#include<stdio.h>
long long check(long long n,long long x){
//这里假设在边的上半部分射入
long long res=n+x+x;
//n+x是所有光线的必经之路
//欸,发现问题,似乎最后一段红色不是必经的
for(long long i=2;;i++){
if(n-i*x>x) res+=2*x;
//判断能否进行重复单元
else if(n-i*x==x){
res+=x;
//恰好能走一个
break;
}
else{
long long cnt=x/(n-i*x);
res+=(n-i*x)*(2*cnt-1);
//加上图中蓝色部分
break;
}
}
return res;
}
int main()
{
long long n,x;
scanf("%lld%lld",&n,&x);
if(2*x>n) x=n-x;//如果从下半部分射入,其实是对称的
printf("%lld",check(n,x));
return 0;
}39.二进制
#include<stdio.h>
#include<math.h>
//计位数,从前向后取
//如果该位数大于7,占位,并继续分解并且占位
//若该位小于等于7,&4 2 1,有就打印2(2)+
//1要特殊输出2(0))
int Cnt(int num){
int cnt=0;
while(num){
//num>>=1;你发现num被强制除以2了
//不论该二进制位上有没有1
//但是好像num--并没有什么luan用
cnt++;
if(num&1) num--;
num>>=1;
}
--cnt;
return cnt;
}
void breakDown(int num){
int cnt=1,flag=0;
int cnt1=Cnt(num);
//不知道为啥,cnt<<=cnt1就不行
cnt=pow(2,cnt1);
while(num){
if(num>7){
flag=1;
//用2(占位
printf("2(");
num%=cnt;
breakDown(cnt1);
cnt1=Cnt(num);
cnt=pow(2,cnt1);
}
else{
while(num){
if(num>=4){
printf("2(2)");
num%=4;
if(num) printf("+");
}
else if(num>=2){
printf("2");
num%=2;
if(num) printf("+");
}
else{
printf("2(0)");
//笔者第一次就忘了更新num导致如下图
num=0;
}
}
}
if(flag==1) {
printf(")");
//记得把flag推倒,不信?试试9呢
flag=0;
if(num) printf("+");
//接着判断是否需要在)后面加+
}
}
}
int main()
{
int num;
scanf("%d",&num);
breakDown(num);
return 0;
}注意循环的嵌套,条件判断的位置,谢谢:(

41~50
41.货运优化
笔者开始总是每用一个新的箱子就想着把1*1的货物装进去,但是先后装的顺序没什么影响,反而让代码变成shi山
此外,也没有必要用二维数组,除了内存之外,每次打字也很麻烦不是吗
特别注意到装3*3货物的情况,向上取整,家人们,都用起来好吗
用绝对值也很方便,不用多次计算多的或者少的空间
#include <stdio.h>
#include<math.h>
int main()
{
int box[7]= {0};
//记录每一次的货物情况
int all[100000]={0};
//记录每一行的货物所需箱子数目
int cnt=0;
while(1){
int flag=0,sum=0,s=0;
for(int i=1;i<7;i++){
//虽然说,应该以0开始计数,但是真的很不适应呀
//放过自己
scanf("%d",&box[i]);
if(i>3) sum+=box[i];
if(box[i]!=0) flag=1;
}
if(flag==0) break;
//有0就终止
sum+=ceil(box[3]/4.0);
//向上取整
int left=box[4]*5-box[2];
//看还能装多少2*2的货物
if(left>=0) box[2]=0;
else box[2]=fabs(left);
int val=0;
switch(box[3]%4){
case 1:val=5;
break;
case 2:val=3;
break;
case 3:val=1;
break;
}
//3*3的货物装完之后最多剩余一个集装箱
left=val-box[2];
if(left>=0) box[2]=0;
else box[2]=fabs(left);
if(box[2]>0) sum+=ceil(box[2]/9.0);
//接下来开始装1*1的货物
for(int k=2;k<7;k++){
s+=box[k]*k*k;
}
left=sum*36-s-box[1];
if(left<0){
sum+=ceil(fabs(left)/36.0);
}
all[cnt++]=sum;
}
for(int i=0;i<cnt;i++)
printf("%d\n",all[i]);
return 0;
}
42.波士顿房价
#include<stdio.h>
//计算x,y的平均值
//计算每一个x*y
//double类型
int main()
{
int house[50][2]={0},n;
double s=0,s1=0,s2=0,s3=0;
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int k=0;k<2;k++){
scanf("%d",&house[i][k]);
if(k==0) {
s1+=house[i][k];
s3+=house[i][k]*house[i][k];
}
else s2+=house[i][k];
}
s+=house[i][0]*house[i][1];
}
s2/=n;
s1/=n;
double up=s-n*s1*s2;
double down=s3-n*s1*s1;
double b=up/down;
double a=s2-b*s1;
printf("Y=%.4lf+%.4lf*X",a,b);
return 0;
}
43.完美矩阵
#include<stdio.h>
#include<math.h>
int main()
{
int n,m,sum=0;
int a[300][300];
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++){
for(int k=0;k<m;k++){
scanf("%d",&a[i][k]);
}
}
int min=m>n?n:m;
//题目有点问题,这里就是寻找符合条件的子方阵
int cnt,flag;
for(int k=2;k<=min;k++){
//k为子方阵的边长
for(int i=0;i<n+1-k;i++){
//假设p为子方阵的第一排最右边的点
//i是最左边的点
//则有,p-i+=k并且p<=n-1
for(int j=0;j<m+1-k;j++){
//核心就是检验以某一点展开的子矩阵是否满足条件
cnt=0,flag=0;
for(int i1=i;i1<k+i;i1++){
for(int j1=j;j1<k+j;j1++){
if(i1==i||j1==j||i1==k+i-1||j1==k+j-1){
if(a[i1][j1]==0) {
flag=1;
break;
}
}else if(a[i1][j1]==1) cnt++;
}
if(flag==1) break;
}
if(flag==0&&fabs((k-2)*(k-2)-2*cnt)<=1) sum++;
}
}
}
printf("%d",sum);
return 0;
}44.托运行李
#include<stdio.h>
//托运两个行李
//随身携带一个,不超过a[][4]
//两个不超过总的重量a[][3]
//ooutput YES NO
//double类型
int main()
{
int bag[40000][5]={0},n;
scanf("%d",&n);
//input
for(int i=0;i<n;i++){
for(int k=0;k<5;k++){
scanf("%d",&bag[i][k]);
}
}
//检查随身携带
//为了尽可能地满足条件,让随身携带的重量最大(满足条件)
for(int i=0;i<n;i++){
int cnt=0,sum=0,along[5]={0};
for(int k=0;k<3;k++){
if(bag[i][k]<=bag[i][4])
along[cnt++]=bag[i][k];
sum+=bag[i][k];
}
if(cnt==0){
printf("NO\n");
continue;
}else{
//据说这叫冒泡排序,就是一步一步把最大的放在最左边
//比如,你可以试着排一下,1 2 3 4
for(int q=1;q<cnt;q++){
for(int j=0;j<cnt-q;j++){
if(along[j]<along[j+1]){
int temp=along[j];
along[j]=along[j+1];
along[j+1]=temp;
}
}
}
sum-=along[0];
if(sum<=bag[i][3])
printf("YES\n");
else printf("NO\n");
}
}
return 0;
}45.计算行列式
移步ac这位学长(也许
但是我是这样子的 wa(泪
#include<stdio.h>
#include<stdlib.h>
void freeMatrix(int **a,int size){
for(int i=0;i<size;i++){
free(a[i]);
}
free(a);
}
//创建子矩阵
int** new(int size){
int **matrix=(int **)malloc(sizeof(int *)*size);
for(int i=0;i<size;i++)
matrix[i]=(int *)malloc(sizeof(int)*size);
return matrix;
}
int calculate(int **matrix,int size){
int ret=0;
if(size==1)
return matrix[0][0];
for(int i=0;i<size;i++){
int **subMatrix=new(size-1);
for(int k=0;k<size-1;k++){
for(int j=0;j<size-1;j++){
if(j<i){
subMatrix[k][j]=matrix[k+1][j];
} else {
subMatrix[k][j]=matrix[k+1][j+1];
}
}
}
int sgn=i%2==1?-1:1;
ret+=matrix[0][i]*sgn*calculate(subMatrix,size-1);
freeMatrix(subMatrix,size-1);
}
return ret;
}
int main()
{
int n;
scanf("%d",&n);
int **matrix=new(n);
for(int i=0;i<n;i++){
for(int k=0;k<n;k++){
scanf("%d",&matrix[i][k]);
}
}
printf("%d\n",calculate(matrix,n));
freeMatrix(matrix,n);
return 0;
}
/*
3
2 6 3
1 0 2
5 8 4*/
46.回文数之和
#include<stdio.h>
#include<stdlib.h>
/*
写一个对n进制进行检查的函数
将每一位分解放入数组中
进行记位数
对前几位和后几位依次进行比较*/
int cnt(int num,int k){
int count=0;
while(num){
num/=k;
count++;
}
return count;
}
int *decompose(int num,int k){
int *pos;
int count=cnt(num,k);
pos=(int*)malloc(sizeof(int)*count);
for(int i=0;i<count;i++){
pos[i]=num%k;
num/=k;
}
return pos;
}
int check(int *pos,int num,int k){
int count=cnt(num,k);
for(int i=0;i<=count/2;i++){
if(pos[i]!=pos[count-i-1]){
free(pos);
return 0;
}
}
free(pos);
return 1;
}
int main()
{
int num,k,sum=0;
scanf("%d%d",&num,&k);
for(int i=1;i<num;i++){
int flag=check(decompose(i,k),i,k)+check(decompose(i,10),i,10);
if(flag==2) sum+=i;
}
printf("%d",sum);
return 0;
}47.稀疏矩阵
难道是我没看清楚吗(苦恼
为什么这里是任意满足即可
#include<stdio.h>
int main()
{
int n,m;
scanf("%d%d",&n,&m);
int number=0;
double cnt=0;
for(int i=0;i<n;i++){
for(int k=0;k<m;k++){
scanf("%d",&number);
if(number!=0) cnt++;
}
}
double judge=(double)(cnt/(m*n));
if(cnt<=m||cnt<=n||judge<=0.05)
printf("Yes");
else printf("No");
return 0;
}49. 蒙特卡洛法求积分
它实际上只取了n-1次函数值,但是除的是n(不理解
#include<stdio.h>
#include<math.h>
//#include<time.h>
#include<stdlib.h>
/*
写五个函数
计算函数的N个值相加*/
double fun(int m,double x){
switch(m){
case 1:
return pow(x,4)*exp(-x);
case 2:
return x*x+1;
case 3:
return cos(x);
case 4:
return sqrt(x)*(x-2);
case 5:
return 2*sin(x)-5*cos(x);
}
return 0;
}
int main()
{
int m,N;
double a,b,sum=0;
scanf("%d%lf%lf%d",&m,&a,&b,&N);
double c=b-a;
srand(RAND_MAX);
for(int i=1;i<N;i++){
//乐
sum+=fun(m,a+((double)rand()/RAND_MAX)*c);
}
printf("%.6lf",c*sum/N);
return 0;
}50.素数筛
移步往期内容,有更详细一点的思路
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
int main()
{
int n,cnt=0;
scanf("%d",&n);
int *prime;
bool *judge;
prime=(int*)malloc(n*sizeof(int)+1);
judge=(bool*)malloc(n*sizeof(bool));
int i,j,k;
for(j=0;j<=n;j++) judge[i]=0;
for(i=2;i<=n;i++){
if(judge[i]==0){
prime[++cnt]=i;
}
for(k=1;k<=cnt;k++){
if(prime[k]*i<=n)
judge[prime[k]*i]=1;
else break;
if(i%prime[k]==0) break;
}
}
printf("%d",cnt);
free(judge);
free(prime);
return 0;
}51~60
55.元宇宙A+B
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
//做元宇宙加法
//对每一位的数字相加,满36进一
void swap(char *str){
int len=strlen(str);
for(int i=0;i<len/2;i++){
char temp;
temp=str[i];
str[i]=str[len-1-i];
str[len-1-i]=temp;
}
}
int main()
{
char str1[15]={'\0'};
char str2[15]={'\0'};
int num1[15]={0};
int num2[15]={0};
//因为字符串只能处理一个字符,而例如9+8结果为两位数,所以考虑再创一个数组
scanf("%s%s",str1,str2);
//注意到只有一行数据 空格隔开
int len1=strlen(str1);
int len2=strlen(str2);
int len=len1>len2?len1:len2;
int temp=0;
swap(str1);
swap(str2);
//为了从低位加到高位
//你也许会说,从高位开始遍历不就可以吗
//那进位怎么办呢?
for(int i=0;i<len;i++){
if(str1[i]=='\0') num1[i]=temp;
//没有这一行的话,如果str1的长度比len小,那么就不会记录进位
if(str1[i]>='0'&&str1[i]<='9'){
num1[i]=str1[i]-'0'+temp;
}
if(str1[i]>='A'&&str1[i]<='Z'){
num1[i]=str1[i]-'A'+10+temp;
}
temp=0;
if(str2[i]>='0'&&str2[i]<='9'){
num2[i]=str2[i]-'0';
}
if(str2[i]>='A'&&str2[i]<='Z'){
num2[i]=str2[i]-'A'+10;
}
num1[i]+=num2[i];
while(num1[i]>35){
num1[i]-=36;
//注意是减36,不是35!
temp++;
if(i+1>=len) len++;
//更新位数
}
}
for(int i=len-1;i>=0;i--){
if(num1[i]>9){
printf("%c",'A'+num1[i]-10);
}else printf("%d",num1[i]);
}
return 0;
}
61~70
68.有效表达式
留个坑。。。
#include<stdio.h>
int triangle[100][100];
int comb(int n,int k);
int main(){
int n;
scanf("%d",&n);
printf("%d",comb(2*n,n)/(n+1));
return 0;
}
//通过组合数的性质求,在杨辉三角形中一个数等于它肩上的两个数字之和
int comb(int n,int k){
if(k == 0 || k == n) triangle[n][k] = 1;
else triangle[n][k] = comb(n-1,k) + comb(n-1,k-1);
return triangle[n][k];
}























 9648
9648

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








