双腕带高尔夫挥杆分析系统

高尔夫挥杆分析系统与双腕带及运动分析算法

摘要

本文开发了一种带有惯性传感器和挥杆动作分析算法的高尔夫姿态分析系统，可用于高尔夫球场。具体而言，我们开发了一种可佩戴于左右手腕的腕带，用于分析佩戴者的高尔夫挥杆动作。通过分析高尔夫球手左右手腕的动作，可以更准确地判断其挥杆动作，从而为高尔夫球手提供挥杆建议。实验结果表明，该便携式设备及其挥杆运动检测算法是一种有前景的高尔夫训练工具。

索引词 —高尔夫挥杆动作，陀螺仪，加速度计，APS，IMU

一、引言

信息技术的进步推动了基于视频或可穿戴传感器的发展，包括动作识别、智能家居系统、医疗保健系统和视频监控[1]‐[6]，这些系统基于人体活动识别提供个人安全和动作识别功能。动作识别利用摄像头传感器或各种其他传感器设备来识别人体移动[7][8]。这些传感器（可穿戴或视频）包括磁力计、陀螺仪和摄像机。

近年来，运动分析领域受到了广泛关注，该技术被广泛应用于体育[9][10]的多种场景中。由于难以在体育技术的所有方面识别出优良的技术，运动员对于提升此类技能具有重要作用。

运动矫正和康复辅助。随着计算能力和速度的提升，计算机研究人员可以利用计算机传感器进行运动动作分析，将运动员的动作与特定动作数据库直接进行比较。此外，运动分析可以提供有关速度和旋转角度的详细数据，以便运动员和教练分析其姿势。

高尔夫是一项越来越多人感兴趣的流行运动。然而，高尔夫挥杆是一种非常快速且复杂的动作，使得高尔夫球手难以识别自己的挥杆动作。如果高尔夫球手能够了解自身的挥杆行为，就可以发掘有用信息，帮助改进挥杆并提高成绩。因此，已经开发出多种高尔夫训练系统，用于捕捉高尔夫挥杆过程中的人体动作，并为训练提供有用信息。

关于高尔夫挥杆追踪系统的研究包括在人体受试者身上放置特殊标记、视觉系统、Kinect、传感器或特殊紧身衣物，这些方法可以通过利用有益数据[10]‐[22]来识别和追踪动作。

标记和光学动作捕捉系统可被视为测量的黄金标准，因为它们能够提供与其他仪器[13][14]相比可靠的旋转和位置。然而，光学动作捕捉系统价格昂贵且需要更大的空间。此外，带有标记的服装可能会干扰受试者，从而可能影响正在测量的体育活动。因此，在分析高尔夫挥杆时，这类系统难以应用。此外，在高尔夫球场的广阔场地中也不实用。最近，许多研究人员试图开发在视频场景中无需直接使用标记的人体动作追踪技术[10]。然而，从背景中获取的人体动作在追踪精度方面尚不够准确，这在动作识别和人体动作分析中尤为明显。此外，当存在与背景颜色相似的颜色时，该技术还存在无法识别动作的缺点。

近年来，由于惯性传感器具有小巧尺寸、低成本和轻重量的特点，基于惯性传感器的高尔夫挥杆动作捕捉已被广泛研究。这些传感器可安装在高尔夫球杆上，以测量高尔夫挥杆的握把角度和握把速度[18][19]；或者安装在身体上，以获取身体旋转和移动信息[20][21]。然而，这些进展在高尔夫球场上的实际应用中并不实用。一种克服此问题的方法是在手腕上佩戴腕带。通过分析双手的动作，可以预测高尔夫球的精确飞行轨迹。

本文中，我们开发了一种带有惯性传感器和挥杆动作分析算法的高尔夫姿态分析系统，可在高尔夫球场使用。具体而言，我们为两只手腕开发了腕带，以分析佩戴者的高尔夫挥杆动作。通过分析高尔夫球手的左右手腕动作，可以更准确地分析其高尔夫挥杆。

本文其余部分组织如下。在第二节中，我们介绍相关工作。第三节介绍了提出的姿态参考系统（ARS）。第四节介绍了提出的算法。在第五节中，我们描述了实验结果。最后，第六节给出了我们的结论。

II. 相关工作

要充分理解高尔夫挥杆，必须单独了解高尔夫挥杆的每个步骤，并开发能够识别高尔夫挥杆动作的算法。

A. 高尔夫挥杆

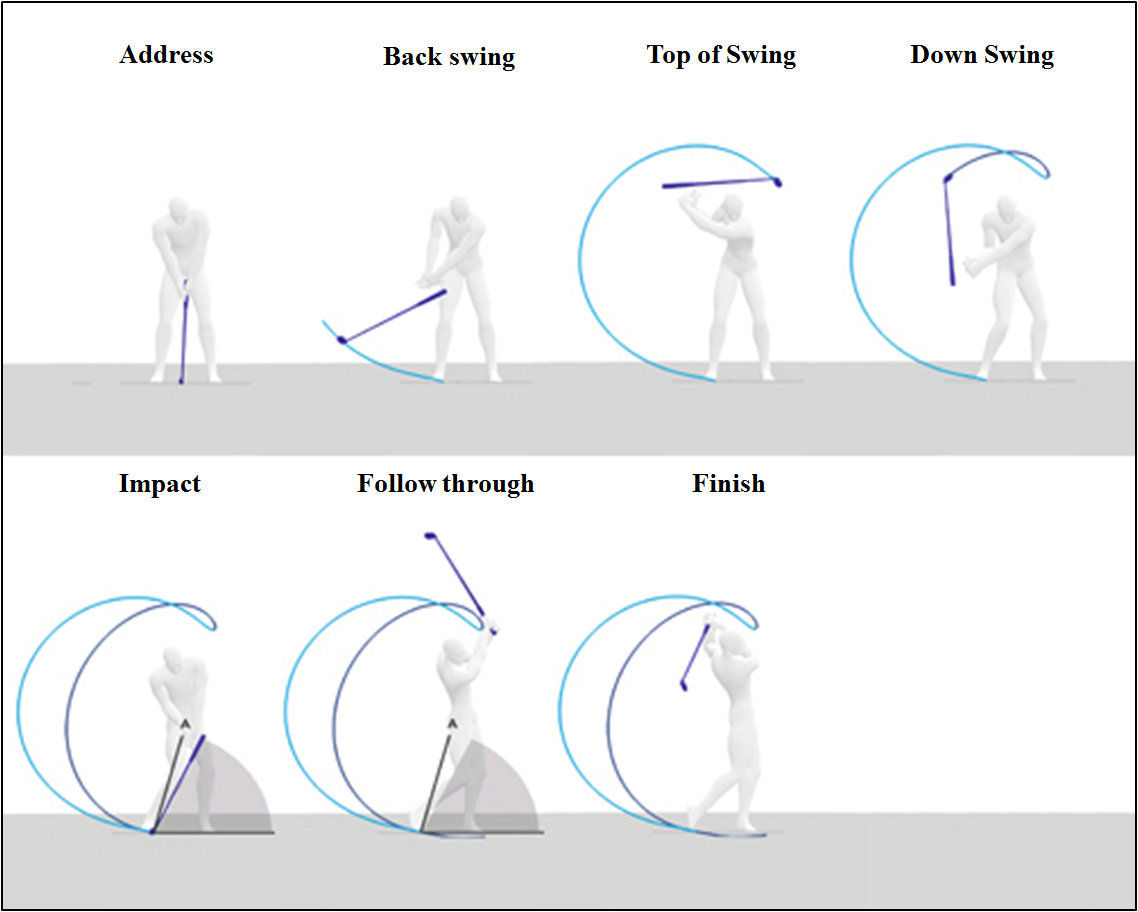
图1显示每次高尔夫挥杆需要7个身体动作步骤：准备姿势、上杆、挥杆顶点、下杆、击球点、随挥和收杆[25]。

如第一个动图所示，高尔夫球手将杆头置于高尔夫球前方。从准备姿势进入上杆动作时，手腕、手臂和肩膀以一定的旋转角度向上移动，同时臀部围绕身体轴线旋转。

在挥杆最高点时，球杆的握把末端达到最高位置，并形成最大旋转角度。从最高点进入下杆动作时，臀部、肩膀、手臂和手腕的扭转或旋转角度逐渐释放，球杆向下挥动。

击球点之后，动作转入随挥，最终到达收杆[24][25]。

B. 姿态参考系统（ARS）

图2展示了姿态参考系统根据动作捕捉设备接收的数据估算出的加速度、位置和方向值。首先，利用从传感器接收的加速度计和陀螺仪传感器数值计算出多个四元数值。具体而言，线性加速度、沿轴的线速度以及位置均被计算为四元数。

系统根据线性加速度、线速度和位置来识别高尔夫挥杆动作，并用于分析高尔夫挥杆动作的准确性。此外，姿态参考系统（ARS）通过三维建模显示挥杆动作分析，同时显示传输的线性加速度、线速度和位置信息，为高尔夫球手提供其挥杆动作的相关信息。红线框内的内容展示了本文提出的高尔夫挥杆动作分析系统及三维建模。ARS各模块的操作算法如下。

四元数

一个四元数是计算使用公式(1)中显示的坐标，通过标量ƞ和向量ɛ进行计算。四元数的逆可以通过改变向量ɛ的符号获得。
$$
q = {\eta, \epsilon} = {\eta, \epsilon_x, \epsilon_y, \epsilon_z}
$$
$$
q^{-1} = {\eta, -\epsilon}
$$
(1)

如公式(2)所示，旋转角度可以用四元数表示。这里，$\theta_x, \theta_y, \theta_z$ 表示物体相对于 $x, y, z$ 的旋转角度。
$$
\theta_x = \arctan\left(\frac{2(\epsilon_1\epsilon_2 + \epsilon_3\epsilon_4)}{1 - 2(\epsilon_2^2 + \epsilon_3^2)}\right)
$$
$$
\theta_y = \arcsin\left(2(\epsilon_1\epsilon_3 - \epsilon_4\epsilon_2)\right)
$$
$$
\theta_z = \arctan\left(\frac{2(\epsilon_1\epsilon_4 + \epsilon_2\epsilon_3)}{1 - 2(\epsilon_3^2 + \epsilon_4^2)}\right)
$$
(2)

转换线性加速度计四元数

全局加速度可以通过将局部加速度旋转到全局坐标来计算。全局坐标的旋转值可以通过四元数获得，旋转矩阵可以表示为公式(3)。其中，R 是旋转矩阵。
$$
R =
\begin{bmatrix}
R_{11} & R_{12} & R_{13} \
R_{21} & R_{22} & R_{23} \
R_{31} & R_{32} & R_{33}
\end{bmatrix}
=
\begin{bmatrix}
1 - 2\epsilon_2^2 - 2\epsilon_3^2 & 2(\epsilon_1\epsilon_2 + \epsilon_3\epsilon_4) & 2(\epsilon_1\epsilon_3 - \epsilon_2\epsilon_4) \
2(\epsilon_1\epsilon_2 - \epsilon_3\epsilon_4) & 1 - 2\epsilon_1^2 - 2\epsilon_3^2 & 2(\epsilon_2\epsilon_3 + \epsilon_1\epsilon_4) \
2(\epsilon_1\epsilon_3 + \epsilon_2\epsilon_4) & 2(\epsilon_2\epsilon_3 - \epsilon_1\epsilon_4) & 1 - 2\epsilon_1^2 - 2\epsilon_2^2
\end{bmatrix}
$$
(3)

从公式(3)得到的旋转矩阵用于计算局部加速度的倾斜加速度，如公式(4)所示。在公式(4)中，Acc是三轴加速度数据，localAcc是基于传感器轴的加速度，而tiltAcc表示相对于全局轴的加速度。
$$
Acc_{tilt} = R \times Acc_{local}
$$
(4)

倾斜加速度是包含重力的物体加速度。通过从倾斜加速度中减去重力，可以得到物体的线性加速度。公式(5)即为线性加速度。其中，linAcc是线性加速度。
$$
Acc_{lin} = Acc_{tilt} - [0,0,9.8]
$$
(5)

转换线性速度

通过对加速度积分可以获得速度。公式(6)表明初始速度被设为零。其中，Vel 是三个轴的速度。
$$
Vel_t = Vel_{init} + \int_0^t Acc_{lin} dt, \quad Vel_{init} = 0
$$
(6)

传感器具有一定的固有误差。每个传感器的误差不同，且由于积分运算误差导致误差增大。此外，积分运算的结果仅在一个方向上增加，这称为漂移效应。如果不知道每个设备的其他误差，我们将应用高通滤波器来减少漂移效应。公式(7)显示了经过高通滤波器后的速度。其中，dt为时间变化，f为频率，rc为截止频率，HP_Vel_ 表示应用高通滤波后的速度。
$$
HP_Vel_t = \alpha \cdot HP_Vel_{t-1} + \alpha \cdot (Vel_t - Vel_{t-1})
$$
$$
\alpha = \frac{dt}{dt + rc}, \quad rc = \frac{1}{2\pi f}
$$
(7)

位置

通过对速度积分可以获得位置。使用公式(8)来获取随时间变化的位置。其中，Pos表示三个轴的位置。
$$
Pos_t = Pos_{init} + \int_0^t HP_Vel dt, \quad Pos_{init} = 0
$$
(8)

为了减小积分动作的漂移效应，还应用了高通滤波器，如公式(9)所示。其中，HPPos_ 是应用高通滤波器后的三轴位置。
$$
HP_Pos_t = \alpha \cdot HP_Pos_{t-1} + \alpha \cdot (Pos_t - Pos_{t-1})
$$
$$
\alpha = \frac{dt}{dt + rc}, \quad rc = \frac{1}{2\pi f}
$$
(9)

III. 所提出的系统

本文使用姿态参考系统来分析高尔夫挥杆动作。姿态参考系统采用了惯性测量单元MPU‐6050。将惯性测量单元采集的数据转换为四元数后，可通过位置、方向和速度四元数来分析高尔夫挥杆的动作。

A. 基于IMU（惯性测量单元）的设备

在本文中，我们开发了如图3所示的所提出的系统，该系统由电源模块、MCU板和硅胶腕带组成。电源模块负责电池的充放电管理。MCU板包含微控制器、传感器和蓝牙。微控制器采用通用处理器。IMU使用具有三轴加速度的加速度计和陀螺仪传感器。加速度灵敏度级别可设置为± 4, ± 8, ± 16 g，陀螺仪的灵敏度可设置为500、1000和2000度。在本文中，我们使用的加速度灵敏度级别为± 16 g，陀螺仪灵敏度级别为2000度。通过传感器测量的六轴数据未经处理即通过蓝牙传输，用于结合传输的数据获取高尔夫挥杆动作。蓝牙模块使用HC06以 115200比特每秒的速率传输数据。本仪器使用的采样率为250赫兹。由于高尔夫球手的球杆速度通常在75英里每小时（120公里/小时）到120英里每小时（192公里/小时）之间，因此杆头每次采样的移动距离为13厘米至21厘米。

收集到的数据可通过电脑或智能手机进行分析，以告知用户其高尔夫挥杆动作的准确性。

B. 坐标系的定义

通过分析从两个腕带获取的数据，可以确定高尔夫挥杆动作的准确性。

图4展示了双腕带在两只手腕上的全局坐标系和局部坐标系的定义。图4(a)显示了全局坐标。当高尔夫球手处于准备击球姿势时，全局坐标系的原点位于握把末端。在水平面上，球的轨迹方向为Y轴，高尔夫球手姿势的前后方向为X轴，垂直方向为Z轴。无论进行何种高尔夫挥杆动作，全局坐标始终保持在同一位置不变。

图4(b) 显示了局部坐标。上方的图显示了右手腕的局部坐标，下方的图显示了左手腕的局部坐标。在水平面中，x轴为手腕的前后方向，y轴为手腕的侧向，z轴为手腕的垂直方向。当采用准备姿势时，局部坐标被初始化。

双腕带识别出高尔夫球手的两只手腕处于该位置，并传输局部坐标。高尔夫挥杆从高尔夫球手采取准备姿势开始，直到收杆结束。挥杆过程中，双腕带实时测量并将数据传输至计算机。双腕带内置加速度传感器，可在高尔夫球手静止时用于预测重力方向。通过将估计的重力方向映射到全局坐标，实现对高尔夫挥杆的分析。

C. 挥杆动作分析系统与三维可视化

所提出的系统在高尔夫挥杆过程中对两只手腕进行分析。如图2所示，利用传输的线速度、线速度和映射后的全局位置坐标进行运动分析和三维建模。速度用于计算当前位置值，在运动分析或三维建模中并不需要。因此，如图5所示，仅使用高尔夫挥杆的加速度和位置信息来进行动作分析。

这七个步骤被分为三组：从准备到顶点、从顶点到击球、从击球到收杆，用于分析目标挥杆动作。特别是，我们的系统会分析七个步骤中的关键部分：上杆、下杆和随挥。高尔夫球手会多次重复高尔夫挥杆以获得平均挥杆数据。系统利用这些测量数据存储每个挥杆步骤的平均线性加速度和位置。所存储的线性加速度和位置数据可与当前挥杆数据进行比较，从而为高尔夫球手提供挥杆建议。通过这种运动分析，高尔夫球手能够正确识别错误的挥杆动作。

我们的系统还使用三维建模来显示挥杆动作。因此，高尔夫球手可以更准确地感知自己的挥杆区间与平均挥杆之间的差异。高尔夫球手能够识别并纠正其平均挥杆中的差异，并利用这些信息来修正自身的挥杆动作。

IV. 实验结果

我们将佩戴腕带在两只手腕上进行高尔夫挥杆的结果进行比较。此外，我们还根据ARS算法对每一步计算的结果进行了比较。该实验旨在确定挥杆动作。

A. 高尔夫挥杆分析

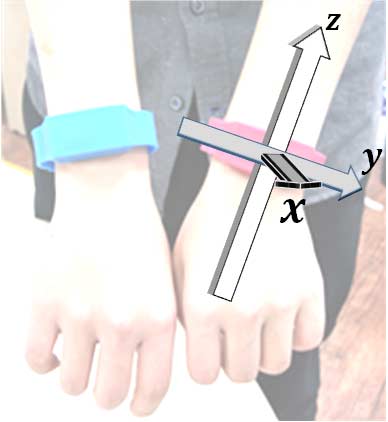
图6显示了基于左右手腕确定高尔夫挥杆动作的过程。首先，根据来自陀螺仪传感器和加速度传感器的数据计算四元数值，如图2所示。四元数包含四个分量，因此我们未尝试对其进行可视化。图6(a)显示了利用获得的四元数和加速度在全局坐标中计算出的倾斜加速度。为了能够准确地进行运动分析，将计算得到的加速度转换为线性加速度。因此，通过对全局坐标的倾斜加速度进行积分，可计算出线性加速度（图6(b)）。该线性加速度用于计算三维建模和姿态分析所需的速度。速度通过线性加速度计算得出。图6(c)展示了各个方向上的线速度。在获得线速度后，执行高通滤波计算以消除噪声并补偿传感器误差。使用高通滤波可以获得去除漂移效应的线速度，如图6(d)所示。此处计算出的线速度用于分析高尔夫动作。

最后，图6(e)显示了用于计算每一步位置的线速度积分。当执行积分结果时，需要使用高通滤波器，因为总会发生漂移现象。图6(f)显示了应用高通滤波器后的位置。高尔夫挥杆动作通过上述过程计算出的速度、坐标和加速度来确定。挥杆姿势可以通过将测量到的挥杆动作与平均挥杆动作进行比较来校正。

B. 高尔夫挥杆的比较

在本文中，我们比较了平均挥杆动作与个人挥杆动作相结合以分析高尔夫球手的挥杆动作。为了得到平均挥杆动作，通过重复20次挥杆计算了挥杆的平均速度和平均位置。

我们计算了平均挥杆与个人挥杆之间的差异。计算了存储的平均挥杆与个人挥杆之间的速度差异。特别是，我们计算了相对于平均挥杆动作的误差。表 I、表 II 和表 III 显示了10次挥杆后每次挥杆与平均挥杆动作的差异结果。

表 I 上杆过程中的平均摆动加速度和个人挥杆加速度误差

No	LEFT X（m/s²）	LEFT Y（m/s²）	LEFT Z（m/s²）	RIGHT X（m/s²）	RIGHT Y（m/s²）	RIGHT Z（m/s²）
1	1.97	1.96	1.04	1.13	1.45	1.20
2	1.21	1.29	0.86	1.15	1.58	1.19
3	0.99	0.59	0.72	0.82	0.57	0.69
4	1.17	0.80	0.82	1.11	0.97	0.74
5	1.89	2.65	2.42	1.45	1.18	1.22
6	1.14	1.68	1.32	1.19	1.12	1.13
7	2.25	2.33	1.96	1.33	0.70	0.78
8	0.93	0.89	0.75	1.42	1.22	1.07
9	1.02	1.17	0.76	1.11	0.50	0.64
10	1.17	0.83	0.85	1.07	0.57	0.88
平均值	1.37	1.42	1.15	1.18	0.99	0.96

表 II 下挥杆期间平均挥杆加速度和个体挥杆加速度误差

No	LEFT X（m/s²）	LEFT Y（m/s²）	LEFT Z（m/s²）	RIGHT X（m/s²）	RIGHT Y（m/s²）	RIGHT Z（m/s²）
1	13.96	17.12	11.20	8.77	13.75	8.31
2	2.31	1.66	1.75	1.46	2.45	0.95
3	1.82	1.31	1.62	2.28	2.77	1.21
4	1.80	1.37	1.95	1.45	2.10	1.15
5	2.60	3.09	2.20	3.06	0.94	2.24
6	3.76	5.05	3.14	1.92	0.67	2.19
7	4.51	4.92	3.33	3.07	2.64	1.00
8	1.91	1.25	1.63	1.64	0.60	2.04
9	1.94	1.20	2.03	1.90	1.21	0.87
10	2.14	3.00	2.00	1.03	1.36	1.16
平均值	3.68	4.00	3.08	2.66	2.85	2.11

表 III 随挥阶段的平均挥动加速度与个体挥动加速度误差

No	LEFT X（m/s²）	LEFT Y（m/s²）	LEFT Z（m/s²）	RIGHT X（m/s²）	RIGHT Y（m/s²）	RIGHT Z（m/s²）
1	2.90	3.36	2.03	3.27	2.27	4.45
2	2.34	2.43	2.18	2.03	2.50	3.43
3	2.33	2.00	2.00	2.81	2.94	3.31
4	2.49	2.19	2.84	2.02	2.90	3.05
5	2.05	2.56	2.07	2.64	3.44	2.83
6	1.95	1.24	2.41	2.33	3.32	2.63
7	2.66	1.92	3.87	2.79	2.68	3.29
8	2.08	2.24	2.16	18.21	24.14	25.01
9	5.50	5.03	5.90	2.51	3.00	2.36
10	2.32	1.85	1.69	2.57	2.96	2.49
平均值	2.66	2.48	2.72	4.12	5.02	5.28

图7比较了左腕上杆、下杆和随挥各阶段的误差，这些数据是根据表 I、表 II 和表 III 计算得出的。图8比较了2号和3号右腕在上杆、下杆和随挥阶段的平均加速度，以及各阶段加速度的误差，这些数据同样基于表 I、表 II 和表 III 的计算结果。在图7和图8中，图像的左侧部分显示平均挥杆的加速度数据，中间部分显示2号与平均挥杆加速度之间的差异，右侧部分显示3号与平均挥杆加速度之间的差异。

表 I、表 II 和表 III 显示了每次挥杆与平均挥杆动作在10次挥杆后的差异结果。其中，左侧的平均挥杆数据是高尔夫球手挥杆20次时，上杆、下杆和随挥阶段的平均挥杆线速度。

分析表格可知，第二次挥杆与平均上杆几乎相似。然而，下杆和随挥的速度略快且力度稍大。可以确认，与其他阶段相比，该阶段相对于平均值的误差较大。特别是可以看出，在下杆过程中x轴的值小于平均值。击球后，球飞向右侧，高尔夫球手意识到这一点，并略微降低了右手腕，以确认x轴的值较小。如图7所示，No2的右手腕图像在上杆阶段与平均高尔夫挥杆加速度值的形状相似。在下杆的100–150样本区间，x轴的值较小，而在随挥的0–40样本区间，x轴的值较大。在下杆过程中，手臂位置略比平均靠前，可以看出随挥时迅速向内拉动。

第三挥杆在上杆阶段与平均挥杆最为相似。然而，在下杆阶段，右手腕的误差大于左手腕的平均值。因此，实际右手腕的移动速度比平均水平更快。我们可以看到杆头向逆时针方向转动，球飞向左方。此外，随挥的速度也快于平均水平。高尔夫球手迅速转动了他们的右手腕击打高尔夫球。在击打高尔夫球的瞬间，杆头速度正确，但球没有直线飞行。

在第6和第7次挥杆期间，段误差相比平均挥杆较大，但所有误差相似，因此高尔夫球的轨迹是直的。在第10次挥杆时，上杆类似，但左挥杆较快，可以看到球向右飞行。

该实验表明，双腕带可用于纠正高尔夫挥杆。

C. 高尔夫挥杆的三维建模

数据分析可用在表 I、表 II、表 III、图7 和图8 中，但此类分析对高尔夫球手而言不易理解。因此，本文通过三维建模，根据高尔夫球手的挥杆展示了平均挥杆的加速度误差和轨迹，如图9所示。

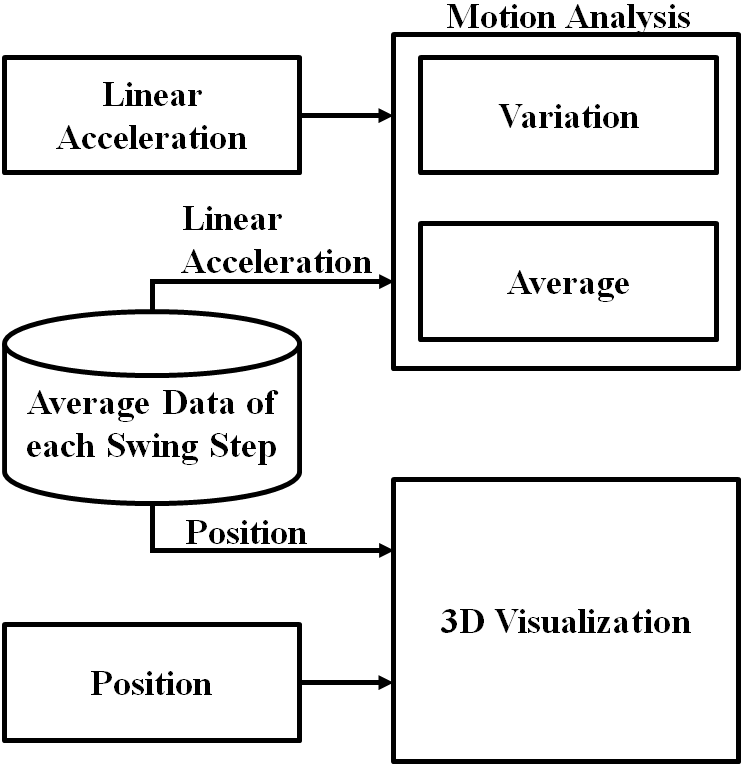
图9显示了通过三维模型得到的2号、3号和平均挥杆中左腕与右腕挥杆轨迹之间的加速度误差。挥杆轨迹中红色部分是平均挥杆与加速度差异较大的部分。图9显示No2和No3的挥杆在下杆时均快速击球。

表 I、表 II、表 III、图7 和图8 显示了相同的结果。如表 I、表 II、表 III、图7 和图8 所分析，图9 (a) 显示在随挥过程中右手腕移动更快。

高尔夫球手可以查看三维模型，了解其高尔夫挥杆的哪些部分与平均挥杆相似，以及他们的挥杆速度是更快还是更慢。此外，通过分析高尔夫挥杆的轨迹并向高尔夫球手提供反馈，可以实现对挥杆的精确分析。对于No2的情况，除击球点时刻的误差外，其余部分的平均挥杆轨迹和加速度均较为相似。

在本文中，高尔夫球手能够判断自己每次挥杆与平均挥杆的偏差程度。此外，通过识别错误的挥杆姿势，还可以指导初学者纠正其高尔夫挥杆动作。

V. 结论

本文中，我们系统的首要目的是通过客观数据识别为高尔夫球手提供建议。第一步是构建一种系统，该系统可以通过在两只手腕上佩戴腕带来分析高尔夫挥杆动作。因此，我们在两只手腕上使用了三维加速度传感器和陀螺仪传感器，以测量每只手腕的角度和线速度。

本文使用两个IMU传感器来确定高尔夫挥杆动作，从而弥补了仅使用安装在球杆或身体上的单个传感器的不足。

实验结果表明，高尔夫球手可以将当前的挥杆动作与平均挥杆动作进行比较。我们证实了可以通过双手腕的挥杆速度和位置信息来调整挥杆动作。

通过向高尔夫球手展示数据的同时还展示三维模型，使得高尔夫球手更容易理解高尔夫挥杆姿势信息。我们的目标之一是将所提出的系统应用于从初学者到专业选手的广泛技能水平的高尔夫球手。在本研究中，我们重点关注了初学者到中级水平的技能水平。

一个未来研究方向是将我们的系统应用于使用双手的各种锻炼，例如游泳和健身。我们还将使用该系统对各种动作进行分类。此外，我们将尝试根据这些分类的动作识别正确行为。