MEC服务器配置优化

移动边缘计算中的服务器配置优化：一种成本‐性能权衡的视角

摘要

在服务提供商构建移动边缘计算（MEC）平台之前，一个需要考虑的重要问题是边缘服务器上计算资源的配置。由于边缘服务器上的计算资源相较于云服务器有限，且服务提供商的部署预算也有限，因此为所有边缘服务器配备充足的计算资源是不现实的。此外，由于地理位置的不同，各边缘服务器的计算需求也存在差异。因此，本文基于选定部署位置的计算需求统计，研究了MEC环境中的服务器配置优化问题。我们的策略是将每个边缘服务器视为一个M/M/m排队模型，并据此建立系统的性能和成本模型。基于所提出的模型，我们提出了两个优化问题：成本约束下的性能优化和性能约束下的成本优化，并通过一系列快速数值算法对其进行求解。我们还进行了大量的数值仿真示例，以验证所提出算法的有效性。MEC服务提供商可利用我们的策略，为每个边缘服务器选择合适的处理器类型并确定最优处理器数量，以实现两个不同目标：（1）在给定成本约束下提供最优质的服务；（2）在保证服务质量的前提下最小化投资成本。本研究对服务提供商控制投资成本与服务质量之间的权衡具有重要意义。

关键词
成本‐性能权衡，边缘服务器，移动边缘计算，排队模型，服务器配置

1 引言

1.1 动机

近年来，移动应用极大地便利了人们的日常生活。人们通过移动应用提供的各种便携式服务进行社交、商务交易、办理公务以及娱乐。与此同时，移动设备（MDs，包括智能手机、手持计算机和其他垂直应用设备）正变得越来越智能和强大，以提供更强的计算能力来支持移动应用。然而，由于便携式设备在空间、电池容量、重量和散热方面的限制，移动设备（MDs）的计算能力仍然有限。随着便携式服务对复杂功能需求的不断增加，移动应用逐渐变得高能耗且计算密集型。将移动应用中的计算密集型任务从移动设备卸载到资源丰富的云，是解决这一问题的有效方法，使得移动用户能够获得高性能服务，同时有效延长设备的电池寿命。

然而，云的数据中心通常位于互联网的核心位置，与移动用户在地理上相距较远，不断增长的移动数据流量给骨干网络带来了巨大负担。随着移动设备（MDs）和移动应用的普及，网络引入的传输延迟已成为新的障碍。这对于一些对任务响应时间敏感的高性能移动应用（例如多人在线游戏、大规模图像处理、个人助手）而言是无法忍受的。事实上，这一挑战将变得更加严峻。根据思科最近的预测，到2023年，全球移动用户总数将从2018年的51亿（占全球人口的66%）增长至57亿（占全球人口的71%）。

作为一种有前景的计算范式，移动边缘计算（MEC）被提出以应对这一挑战。通过在移动基站内部或附近部署边缘服务器，MEC能够在移动网络边缘提供高质量、高带宽和低延迟服务。移动设备通过移动网络直接连接到边缘服务器，并将部分任务（即可卸载任务）在一跳范围内卸载到边缘服务器，从而减轻骨干网络的负载并延长其电池寿命。与云计算平台提供的服务相比，MEC平台所提供的服务具有无与伦比的用户体验质量。因此，MEC正受到学术界和工业界的越来越多的关注。

在服务提供商构建MEC平台之前，一个需要考虑的重要问题是边缘服务器上计算资源的配置。由于边缘服务器上的计算资源相比云服务器有限，且服务提供商的部署预算有限，因此为所有边缘服务器配备充足的计算资源是不现实的。此外，由于地理位置的不同，各边缘服务器的计算需求也不同。当边缘服务器配备的计算资源超过其计算需求时，部分可用计算资源将处于空闲状态。这些空闲计算资源会产生大量浪费性功耗，从而增加服务提供商的运营成本。根据最近的一项研究，服务器在空闲状态下的基本能耗占满载状态下服务器能耗的60%以上。因此，如何优化边缘服务器的计算资源配置（即服务器配置优化），对于MEC服务提供商控制投资成本与服务质量之间的权衡具有重要意义，也是MEC发展中亟待解决的关键问题。

1.2 我们的贡献

在本文中，我们研究了MEC环境中服务器配置优化的问题，其主要目标是根据给定的计算需求统计，优化边缘服务器上配置的处理器数量和类型。我们从服务提供商的角度考虑这样一个典型的应用场景：将在选定的基站部署边缘服务器以建立MEC平台。我们的投资预算是有限的，并希望系统建成后能够提供服务质量保证。因此，我们主要考虑两个关键因素，即系统性能和投资成本。

本文仅关注系统性能而非应用性能。这主要是因为在MEC环境中，移动应用提供的便携式服务多种多样，MEC服务提供商需要从整体角度考虑性能，即系统性能。我们采用平均响应时间作为系统性能指标。另一方面，服务提供商的投资成本包含多个部分，如设备采购、运营成本、维护成本、公用事业成本等。这些成本具有不同的量纲单位。为解决这一问题，我们假设MEC平台的经济寿命为3年，并在本文中采用单位成本作为投资成本指标。

然而，优化性能和成本可能是相互冲突的要求。性能的提升通常伴随着功耗的增加，而功耗是我们的投资成本的重要组成部分。因此，我们考虑投资成本与系统性能之间的权衡，即在给定的系统单位成本约束下最小化平均响应时间，以及在给定的平均响应时间约束下最小化系统单位成本。

平均响应时间约束。本研究的根本目的是找到一种边缘服务器的最优配置，以减少因空闲计算资源导致的冗余投资成本和能耗，并尽可能满足不同部署位置的潜在计算需求，从而降低多个边缘服务器之间任务迁移所引起的通信延迟。

需要注意的是，本文假设不同部署位置的计算需求统计是已知的。尽管由于地理位置的不同以及移动设备的移动性，边缘服务器的工作负载各不相同且动态变化，但我们认为可以通过对基站的历史移动数据流量进行时间序列分析，来预测边缘服务器在较长时间内的稳定计算需求，这部分内容不在本文讨论范围之内。实际上，我们的策略是在系统部署前求解一个服务器配置的静态优化问题，以获得最优服务器配置方案，并可在环境未发生显著变化前长期使用该方案。当经过一段时间后边缘服务器面临的计算需求发生较大变化时，我们可以再次利用该策略获得新的方案并继续使用。

本文的主要贡献可以总结如下。
- 我们建立了一个具有无限等待队列容量的M/M/m排队模型来刻画多个异构边缘服务器，并分别建立了MEC系统的性能模型和成本模型，从而能够解析地计算系统的性能和投资成本。
- 我们提出了两个优化问题，即成本约束下的性能优化（即在给定的系统单位成本约束下最小化平均响应时间），以及性能约束下的成本优化（即在给定的平均响应时间约束下最小化系统单位成本），从而可以从成本‐性能权衡的角度研究边缘服务器的服务器配置优化问题。我们还将这两个问题扩展到服务提供商在构建MEC系统前可从不同硬件供应商提供的多种类型处理器中进行选择的情形。
- 我们设计了一系列基于二分法算法的快速数值算法来解决上述问题。MEC服务提供商可以使用我们的算法选择合适的处理器类型，并为每个边缘服务器获得最优处理器数量，以实现两个不同的目标：（1）在给定成本约束下提供最优质的服务；（2）在保证服务质量的前提下最小化投资成本。
- 我们还进行了大量的数值仿真示例，以展示所提出算法的有效性。

据我们所知，这项工作是首次研究考虑成本‐性能权衡的MEC中服务器配置优化。因此，我们的研究成果为MEC中的计算资源配置问题提供了理论与实践贡献，可应用于MEC平台的部署。

本文的其余部分安排如下。在第2节中，我们回顾了相关工作，并总结了本研究的独特特征。在第3节中，我们定义了两个优化问题（即成本约束下的性能优化和性能约束下的成本优化），用于研究服务器配置问题，并基于排队论建立系统模型。在第4节中，我们对上述优化问题进行建模，并为每个问题开发了一种数值方法和一系列算法。在第5节中，我们进行了大量的数值仿真示例，以验证所提出算法的有效性。在第6节中，我们对本文进行总结，并展望了一些未来研究的方向。

2 相关研究

MEC有两个基本目标，即提高性能和降低成本或功耗，因为低性能会限制移动应用的功能并降低用户体验质量，而高能耗则可能导致严重的经济损失和环境问题。具体而言，有若干关键因素会影响MEC平台的性能和功耗，例如可用计算资源的数量、空闲计算资源的数量、任务卸载量、卸载任务调度、边缘服务器和移动设备的CPU周期频率，以及用于计算卸载的传输/通信速度等。因此，已有大量文献研究了如何从不同切入点考虑各种因素来优化性能和能耗，例如computation offloading optimization、power allocation optimization、dynamic resource allocation optimization等。在本节中，我们主要回顾相关从这三个切入点出发的研究。关于基于其他切入点的相关研究和详细综述，请参见参考文献11‐15、17、18。

计算卸载优化 。计算卸载的基本原理是权衡任务在移动设备和边缘服务器上的执行收益，合理进行任务分割与调度，从而加快计算速度并节省能量。大量文献针对任务分割、分配与执行等方面研究了这一问题。吕等人研究了云、边缘服务器和设备三层架构下的计算卸载策略。作者们提出了一种计算卸载算法，在满足移动设备延迟要求的同时最小化设备的能耗。谭等人在MEC环境中提出了一种负载均衡方案，在满足无线信道容量和链路竞争约束的前提下，最小化可卸载任务的响应时间。在文献21中，作者利用KKT条件，基于不同时隙的功耗和带宽容量实现了任务卸载策略。在文献22中，作者设计了一种面向多用户的分布式计算卸载算法，以最小化全系统计算开销。黄等人设计了一种计算卸载算法，在保证服务质量的前提下最小化系统功耗。类似的问题在文献24和25中也有研究。

在文献26中，Li建立了一个具有无限等待队列容量的M/G/1排队模型，用于刻画多个异构移动设备和边缘服务器，从而能够解析地计算MEC平台的性能和能耗。他研究了MEC环境中的计算卸载策略优化，以平衡功耗与性能。该工作采用了两种不同的CPU核心速度模型，即空闲速度模型和恒定速度模型，来分析移动设备的能耗，从而扩大了该策略的应用范围。他还研究了在MEC环境中多个移动用户进行非合作博弈情况下的计算卸载策略，并设计了一种能够找到纳什均衡的算法来解决此问题。

功率分配优化 。在MEC环境中，不仅需要关注远程基础设施的能耗，还需要关注与移动设备电池寿命相关的MDs能耗。因此，有必要对边缘服务器和移动设备进行合理的功率分配。毛等人提出了一种有效策略，旨在提升系统性能并实现绿色计算，以联合获得可卸载任务的最优调度、移动设备的最优功率分配以及传输功率分配的最优解。他们的算法通过动态调整移动设备的CPU周期频率、卸载决策以及移动设备的发射功率来实现。在文献29中，作者们提出了一种任务卸载的优化框架，该框架联合优化任务分配和移动设备的CPU周期频率，以最小化响应时间和移动设备的功耗。张等人开发了一种任务调度算法，以联合获得移动设备处理器的最优频率和传输功率分配的最优解，从而管理功耗‐性能权衡。李建立了M/G/1排队模型来刻画多个移动设备，并建立M/G/m排队模型来刻画一个边缘服务器。他通过构建非合作博弈框架，对竞争性移动边缘计算环境的稳定性进行了定量研究。在他的工作中，所有移动设备和移动边缘云均可通过动态调整CPU周期频率、卸载决策和传输功率分配，获得使其支付最小的最优动作。

动态资源分配优化 。在MEC中进行动态资源分配优化也是提高性能和降低成本的有效方法。在MEC环境中，可以动态分配多种类型的资源，包括服务器缓存、通信资源（例如无线带宽、通信信道）以及计算资源（例如容器和虚拟机）。张等人提出了一种策略，通过联合优化计算与通信资源分配来管理MEC网络中的能耗与延迟之间的权衡。Xu等人研究了MEC网络中的服务缓存优化问题，并设计了一种算法以确定哪些服务需要在边缘服务器上缓存，从而在给定的能耗约束下提升系统性能。在参考文献33中，作者们开发了一种算法，通过联合优化任务调度、移动设备的发射功率和边缘服务器资源分配来提高卸载增益。然而，他们的工作中计算资源仅通过边缘服务器的计算速率进行抽象表示。Ma等人设计了一种最优资源供应算法，联合确定云资源的利用率和最优边缘计算能力，以最小化服务提供的成本。但该工作仅使用一个简单参数来抽象边缘计算能力。毛等人开发了一种动态资源分配算法，联合获得计算卸载的最优发射功率与带宽分配，从而使任务卸载更有效。Zhou等人设计了一种策略，在虚拟机部署过程中动态调整CPU和内存资源，以最大化能效并最小化SLA违规率。Pašˇcinski等人设计了一种新的自主编排架构，并实现了全局集群管理器（GCM），用于实时监控相关应用程序的选定服务质量指标，从而在软件定义数据中心（SDDC）内自动选择地理上最优的计算资源，最终实现高服务质量。

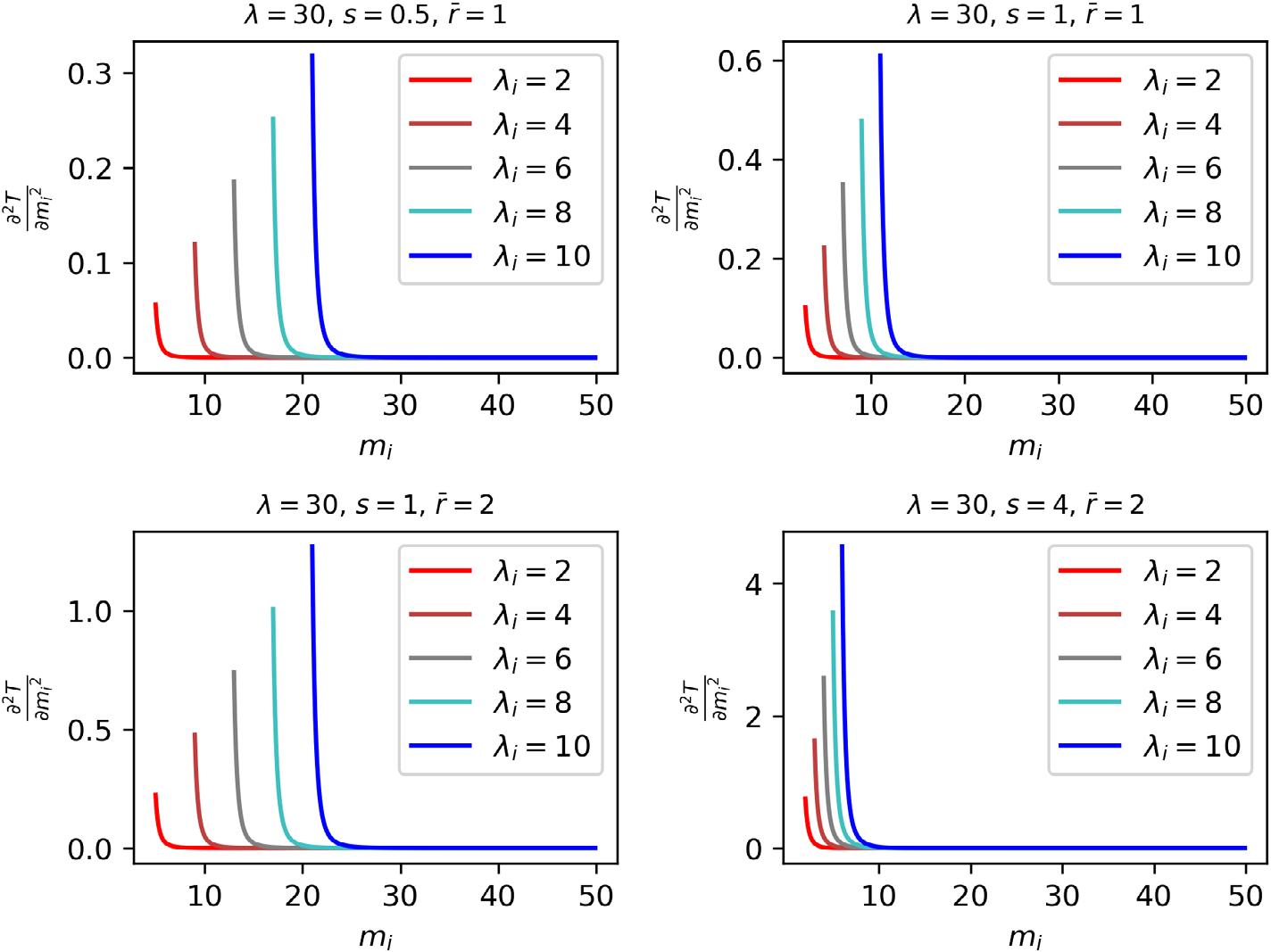
表1 与现有研究的比较表

适用阶段	主要约束	优化目标
计算卸载优化	MEC已建立	性能约束，能量消耗约束
功率分配优化	MEC已建立	性能约束，能耗约束
动态资源分配优化	MEC已建立	资源约束，性能约束，能耗约束
我们的研究	部署前	性能约束，成本约束

从上述文献综述可以看出，大多数现有研究都是在MEC平台已部署的前提下，针对不同的优化目标展开的。我们的工作与上述研究不同，我们考虑的是服务提供商在系统部署前的服务器配置策略。为了明确界定我们的研究，并突出本研究与现有研究之间的差异，我们在表1中进行了对比。

我们的研究具有以下独特特点。
- 我们从服务提供商的角度考虑一个应用场景，即在选定的基站中部署多个边缘服务器以构建MEC平台。由于我们的投资预算是有限的，并且系统在建立后需要提供服务质量保证，因此我们需要根据经过充分分析和预测的计算需求统计，确定在边缘服务器上配置的处理器的最佳数量和类型。
- 我们建立了M/M/m排队模型来描述多个边缘服务器，以便对卸载任务的平均响应时间（包括任务等待时间和任务处理时间）进行严格分析。
- 我们从设备采购（即处理器）、公用事业成本、维护成本和运营成本（即边缘服务器处理器的能耗）等多个方面分析投资成本，并使用单位成本来统一这些成本的不同量纲单位。
- 我们的策略能够提供一种最优服务器配置方案，以减少因空闲计算资源导致的冗余投资成本和能耗，以及因多个边缘服务器之间的任务迁移引起的通信延迟。

需要说明的是，我们的策略与其他优化方法（包括计算卸载优化、功率分配优化和动态资源分配优化）并不冲突，因为我们的策略与其他优化方法应用于MEC系统实施的不同阶段。在系统部署之前，MEC服务提供商可以根据我们的策略控制投资成本与系统性能之间的权衡，并对系统的性能和成本进行定量分析。在所有边缘服务器部署了适当的计算资源之后（即MEC平台已建立），可以从其他角度应用其他优化方法，以进一步提升系统性能或节约能耗。

3 问题定义与模型

3.1 问题定义

我们从服务提供商的角度考虑这样一个典型的应用场景：我们将在n个选定的基站部署S₁, S₂, …, Sₙ边缘服务器，以建立一个MEC平台。此外，我们假设通过基于历史移动数据流量的时间序列预测分析，获得了n个基站的稳定计算需求统计λ₁, λ₂, …, λₙ。我们的投资预算是有限的，并希望系统在建成后能够提供服务质量保证。我们的目标是解决以下两个问题。
- 成本约束下的性能优化 。在给定的成本约束C和上述条件下，确定在每个边缘服务器上配置的处理器的最优数量和类型，以使系统的平均响应时间最小化。
- 性能约束下的成本优化 。在给定的性能约束T̃和上述条件下，确定每个边缘服务器上配置的处理器的最优数量和类型，以使系统的单位成本最小化。

例如，图1表示一个小型MEC环境。在该环境中，我们将在选定的基站（如图1中的A和B）部署两个边缘服务器（如图1中的S₁和S₂），以建立系统。这些选定的基站位于高人口密度区域（如商业和住宅区），具有较高的潜在计算需求。未部署边缘服务器的基站（如图1中的C和D）将把其覆盖范围内移动设备的计算任务迁移到最近的边缘服务器进行处理（如图1中红色虚线箭头所示）。假设A的稳定计算需求（包括C的任务迁移）为λA，B的稳定计算需求（包括D的任务迁移）为λB。我们的主要目标是根据这两个边缘服务器各自的潜在计算需求λA, λB，确定处理器的最优数量和类型，使得在投资成本不超过给定成本约束的前提下，系统的平均响应时间最小；或在平均响应时间不超过给定性能约束的前提下，系统的单位成本最小。

为了解决上述两个问题，并对MEC平台的性能和投资成本进行严谨分析，我们首先需要建立数学模型。

3.2 边缘服务器模型

在MEC环境中，每个边缘服务器配置了不同数量的处理器，并具有不同的计算能力，因此这些边缘服务器是异构的。我们采用M/M/m排队模型来描述多个异构边缘服务器。设服务器Sᵢ上配置的相同处理器数量为mᵢ，即服务器处理器具有相同的执行速度s，单位为十亿条指令每秒（BIPS）。边缘服务器建模如下。

每个边缘服务器在忙于处理任务时，会维护一个具有无限容量的先进先出（FIFO）队列来缓存等待任务，并对到达的任务采用先到先服务（FCFS）的排队规则。随着现代计算机技术的发展，服务器内存变得越来越充足，且MEC系统中的任务响应时间并不很长，因此服务器缓冲区溢出在一定程度上可以忽略。此外，可卸载任务的到达时间具有随机性，其概率分布难以准确获知。然而，自然界中许多事件的发生服从泊松分布，许多其他概率分布也可用泊松分布近似。因此，我们假设每个边缘服务器接收的具有泊松分布的独立任务流（包括其覆盖区域内的用户任务以及从其他基站迁移来的任务），即到达Sᵢ的任务平均到达率为λᵢ，且到达Sᵢ的任务的到达间隔时间是一组独立同分布的指数随机变量，其平均值为1/λᵢ。可卸载任务所需执行的指令数（以十亿条指令为单位）是一组独立同分布的指数随机变量r，其平均值为r。因此，处理器的任务执行时间（以秒为单位）的平均值为x = r/s，即一个可卸载任务被分配给一个空闲处理器执行，直到完成为止。

根据排队论，我们可以得到每个边缘服务器的平均服务速率为 μ = 1/x = s/r。μ的值表示每个处理器每秒执行的任务的平均数量。我们还得到了Sᵢ的服务器利用率：
ρᵢ = λᵢ / (mᵢμ) = λᵢx / mᵢ = λᵢr / (mᵢs), (1)
表示Sᵢ处于繁忙状态的平均时间比例。注意，mᵢρᵢ = λᵢx = λᵢr/s的值表示在Sᵢ上执行任务的处理器的平均数量。

3.3 性能模型

在本节中，我们讨论如何表征MEC系统的性能。具体而言，我们使用平均响应时间作为性能指标。

根据排队论，在服务器Sᵢ的M/M/m排队系统中，有k个任务处于等待或执行状态的概率为
pᵢ,ₖ =
{
pᵢ,₀ (mᵢρᵢ)ᵏ / k!, k ≤ mᵢ;
pᵢ,₀ mᵢᵐⁱ ρᵢᵏ / mᵢ!, k ≥ mᵢ;
}
(2)
其中
pᵢ,₀ = (Σₖ₌₀ᵐ⁻¹ (mᵢρᵢ)ᵏ / k! + (mᵢρᵢ)ᵐⁱ / mᵢ! ⋅ 1/(1−ρᵢ))⁻¹. (3)

然后，我们得到新到达的任务必须被排队的概率为
Pq,ᵢ = Σₖ₌ₘᵢ^∞ pᵢ,ₖ = pᵢ,ₘᵢ / (1−ρᵢ) = pᵢ,₀ mᵢᵐⁱ / mᵢ! ⋅ ρᵢᵐⁱ / (1−ρᵢ). (4)

设Lᵢ表示Sᵢ中任务的平均数量。然后我们有
Lᵢ = Σₖ₌₀^∞ k pᵢ,ₖ = mᵢρᵢ + ρᵢ / (1−ρᵢ) Pq,ᵢ. (5)

应用利特尔法则，Sᵢ的平均任务响应时间为
Tᵢ = Lᵢ / λᵢ = x + Pq,ᵢ / (mᵢ(1−ρᵢ)) x = x(1 + Pq,ᵢ / (mᵢ(1−ρᵢ))). (6)

通过上述分析，我们可以得到系统的平均响应时间（以秒为单位）为
T = Σᵢ₌₁ⁿ (λᵢ / λ) Tᵢ = (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + … + (λₙ / λ) Tₙ, (7)
请注意方程（7）实际上是服务器规模m₁, m₂, …, mₙ的函数，即T(m₁, m₂, …, mₙ).

3.4 成本模型

在本节中，建立了一个分析模型来描述MEC系统的投资成本。

投资成本主要包含两个部分，即静态成本和动态成本。其中，静态成本主要来自硬件设备的采购以及边缘服务器的场地租金，还包括维护成本和公用设施（如空调）成本。然而，我们不考虑场地租金的影响，这主要是因为场地租金在部署位置选定后即已确定。动态成本主要来自边缘服务器处理器的能耗。需要注意的是，静态成本和动态成本具有不同的量纲单位。为解决这一问题，我们假设MEC平台的经济寿命为3年。本文采用系统单位成本作为成本指标。

设Cₛ表示系统的静态成本。我们有
Cₛ = (1+ω)cₚ Σᵢ₌₁ⁿ mᵢ, (8)
其中，cₚ表示速度为s的处理器的价格（以人民币计），ω表示维护和公用事业成本的比率系数（即维护和公用事业成本与边缘服务器规模呈线性关系）。因此，系统的静态单位成本为
C̄ₛ = (1+ω)cₚ Σᵢ₌₁ⁿ mᵢ ⋅ κ⁻¹, (9)
其中κ = 94,608,000是一个常数（3年 ⋅ 365天 ⋅ 24小时 ⋅ 60分钟 ⋅ 60秒），表示3年的总秒数。处理器的功耗主要由三部分组成，即动态功耗、静态功耗和短路功耗。动态功耗是主要组成部分，可以近似为
P_d = aC_esV_p²f_p,
其中，a为活动因子，C_es、V_p和f_p分别为处理器的有效开关电容、供电电压和时钟频率。对于处理器速度s，我们有s ∝ f_p。由于P_d ∝ f_p^α，其中α约等于3，为了便于讨论，我们使用s^α表示速度为s的处理器的动态功耗。请注意，本文中所有数值示例均设α = 3。

此外，处理器的动态功耗与其工作模型相关。根据一些现有研究，处理器通常具有两种工作模式，即空闲速度模型和恒定速度模型。当没有任务执行时，空闲速度模型的处理器速度为零，而恒定速度模型的处理器速度为s。由于服务提供商拟使用的处理器类型/工作模型尚不确定，本文采用这两种核心速度模型以提高策略的适用性。

根据方程（1），我们将具有速度s（单位为瓦特/秒）的处理器的平均功耗建模为
Pᵢ = mᵢ(ρᵢs^α + P ) = λᵢr s^(α−1) + mᵢP , (10)
对于空闲速度模型以及
Pᵢ = mᵢ(s^α + P ), (11)
对于恒定速度模型，其中P 表示速度为s的处理器的基本功率（包括静态功耗和短路功耗）。注意，在方程(10)中，当处理器处于空闲状态时，处理器速度为零，因为s^α乘以了Sᵢ的利用率。因此，我们可以得到系统的动态单位成本
C_d = c_e Σᵢ₌₁ⁿ Pᵢ, (12)

4 我们的解决方案

4.1 成本约束下的性能优化

在本节中，我们解决成本约束下的性能优化问题，即最小化
T(m₁, m₂, …, mₙ) = Σᵢ₌₁ⁿ (λᵢ / λ) Tᵢ = (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + … + (λₙ / λ) Tₙ
（表示所有边缘服务器任务响应时间的加权平均值），需满足约束条件 ρᵢ < 1（因为每个边缘服务器的负载不得超过其容量），对于所有 1 ≤ i ≤ n，即 mᵢ > λᵢx = λᵢr/s；以及 C = C̃（表示投资成本必须接近给定的成本约束）。

为了便于推导，我们对方程(14)和(15)进行简单的变换，并引入一个新的函数 G(m₁, m₂, …, mₙ) 来表示系统单位成本，即
G(m₁, m₂, …, mₙ) = Σᵢ₌₁ⁿ mᵢ = (C̃ - λr s^(α−1) cₑ) / ((1+ω)cₚ / κ + cₑP ), (16)
对于空闲速度模型，以及
G(m₁, m₂, …, mₙ) = Σᵢ₌₁ⁿ mᵢ = C̃ / ((1+ω)cₚ / κ + (s^α + P ) cₑ), (17)
对于恒定速度模型。

我们利用拉格朗日乘子法来解决此优化问题。然而，该方法将服务器规模 m₁, m₂, …, mₙ 视为一系列连续值，而处理器的数量只能是正整数。我们将在算法设计中讨论如何解决此问题，并暂时将服务器规模视为连续变量。

使用拉格朗日乘子法，我们推导出该优化问题的拉格朗日函数为
∇T(m₁, m₂, …, mₙ) = φ∇G(m₁, m₂, …, mₙ),
即，n个方程
∂T(m₁, m₂, …, mₙ) / ∂mᵢ = φ ∂G(m₁, m₂, …, mₙ) / ∂mᵢ,
对于所有 1 ≤ i ≤ n，其中 φ 是一个拉格朗日乘子。根据方程(7)、(16)和(17)，我们得到 ∂T / ∂mᵢ = (λᵢ / λ) ⋅ (∂Tᵢ / ∂mᵢ) = φ, (18)
对于所有 1 ≤ i ≤ n。注意上述 ∂G/∂mᵢ = 1，其在空闲速度模型和恒定速度模型中是相同的。

我们直接使用之前一项工作的结果，即
∂Tᵢ / ∂mᵢ = - (r/s) ⋅ [√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1] / [mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²] (19)
（为了确保本文的可读性，我们在附录中提供了上述方程的详细推导过程）。

根据方程(18)和(19)，我们可以得到
∂T / ∂mᵢ = - (λᵢr / λs) ⋅ [√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1] / [mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²] = φ. (20)

只需证明T是mᵢ的递减函数（即 ∂T/∂mᵢ < 0），因为方程(20)中的每一项均为正，除了开头的负号，即 λᵢr/λs > 0、√(2πmᵢ(1−ρᵢ)) > 0、(eρᵢ/e^(ρᵢ))^(mᵢ) > 0、(ρᵢ+ 3)/2 > 0和 -mᵢ(1−ρᵢ)ln ρᵢ > 0，其中 ρᵢ < 1（即 1−ρᵢ > 0和ln ρᵢ < 0）。

此外，根据方程(14)和(15)，显然C是mᵢ的增函数。因此，随着mᵢ的增加，系统性能将提升，但投资成本也会增加。注意到方程(20)实际上是mᵢ的函数，即φ(mᵢ)。要获得φ(mᵢ)的反函数较为困难。然而，根据我们的观察发现，T是mᵢ的凸函数，且φ(mᵢ)是mᵢ的增函数，因为方程(20)中分子的增长速率低于分母的增长速率，以及 ∂T/∂mᵢ < 0。

为进一步为了说明上述观察结果，我们取二阶偏导数 ∂²T/∂mᵢ²，即
∂²T / ∂mᵢ² = - (λᵢr / λs) (-2Fᵢ³ / Qᵢ² + Fᵢ² ∂Qᵢ / ∂mᵢ), (21)
其中
Qᵢ = √(2πmᵢ(1−ρᵢ)) Hᵢ (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1. (22)
由于
∂Fᵢ / ∂mᵢ = -Fᵢ / (2Qᵢ),
方程(21)可以重写为
∂²T / ∂mᵢ² = - (λᵢr / λs) (-2Fᵢ³ / Qᵢ² + Fᵢ² ∂Qᵢ / ∂mᵢ). (23)
很明显
∂Qᵢ / ∂mᵢ = √(π / (2mᵢ)) (1−ρᵢ) Hᵢ (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + √(2πmᵢ) ρᵢ / mᵢ Hᵢ (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) - Hᵢ ln ρᵢ ⋅ √(2πmᵢ(1−ρᵢ)) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + (1− ln ρᵢ − ρᵢ(2mᵢ+ 1) / (2mᵢ)) √(2πmᵢ(1−ρᵢ)) Hᵢ. (24)
事实上，∂²T/∂mᵢ²是mᵢ的函数。然而，基于数学推导分析 ∂²T/∂mᵢ²的正负性较为困难。因此，我们分别将2.0赋给 λ₁，4.0赋给 λ₂、…，10.0赋给 λ₅，即 λ = 30，然后在mᵢ从 ⌈λᵢr/s⌉（因为mᵢ > λᵢr / (λ₅s)）到50的范围内，获得相应的 ∂²T/∂mᵢ²。通过在坐标轴上绘制这些点，我们得到图2。可以观察到，随着mᵢ的增加，∂²T/∂mᵢ²从正值逐渐趋近于0。这与我们之前的观察结果一致。

由于该优化问题难以获得闭式解，因此在本节中，我们提出一种基于二分法算法的数值解法，分别在一定范围内搜索φ和mᵢ。

由方程（1）可得，对于所有 1 ≤ i ≤ n，mᵢ > λᵢr/s成立。因此，mᵢ的下界为
lbᵢ = ⌈λᵢr/s⌉.

由于φ(mᵢ)是mᵢ的增函数，令lb_max表示lbᵢ的最大值，即
lb_max = max₁≤ᵢ≤ₙ (lbᵢ),
基于方程(20)，我们得到φ的下界
lb_φ = φ(lb_max).
下界mᵢ（即，ubᵢ）和 φ的上界（即，ub_φ）可以通过重复将对应的下界加倍直到C > C̃系统单位成本。

总结上述讨论，给定n、λᵢ、s、r、cₚ、cₑ、ω、P*以及 C̃，我们用于寻找最优处理器配置m₁, m₂、…、mₙ以在给定成本约束C下最小化系统平均响应时间的算法可由算法1–4描述。

算法1. 查找 lb_φ
1: 输入: n, λ₁, λ₂, · · ·, λₙ, s, r̄。
2: 输出: lb_φ。
3: lb_φ, lb_max ← 0; λ ← λ₁ + λ₂ + · · · + λₙ; //初始化参数
4: for i in range(n): //查找所有 1 ≤ i ≤ n 中 lbᵢ 的最大值
5: lbᵢ ← ⌈λᵢr̄/s⌉;
6: if lbᵢ > lb_max:
7: lb_max ← lbᵢ;
8: end if
9: end for
10: lb_φ ← φ(lb_max); //该值由公式(20)计算得出，其中 mᵢ ← lb_max
11: return lb_φ。 //返回 φ 的下界

算法2. 查找 mᵢ，满足 φ
1: 输入：λᵢ, s, r̄, φ。
2: 输出：mᵢ。
3: ε ← 一个非常小的量；lbᵢ, ubᵢ ← ⌈λᵢr̄/s⌉； //初始化 ε, lbᵢ, 和 ubᵢ
4: while φ(ubᵢ) < φ: //φ(ubᵢ)的值由公式(20)计算得出，其中mᵢ ← ubᵢ
5: ubᵢ ← 2ubᵢ; //通过将自身翻倍，直到计算出的φ值大于给定值，来寻找mᵢ的上界
6: end while
7: while ubᵢ − lbᵢ > ε: //在[lbᵢ,ubᵢ]范围内使用二分法算法搜索mᵢ
8: mid ← (lbᵢ + ubᵢ) / 2;
9: if φ(mid) < φ: //φ(mid)的值由公式(20)计算得出，其中mᵢ ← mid
10: lbᵢ ← mid;
11: else:
12: ubᵢ ← mid;
13: end if
14: end while
15: mᵢ ← (lbᵢ + ubᵢ) / 2;
16: return mᵢ。 //当给定φ时，返回Sᵢ的处理器数量

算法3. 查找_配置_，满足_成本_约束
1：输入：C̃, n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P*, idle。//idle 是一个布尔值，表示处理器的工作模型
2：输出： m₁, m₂, · · ·, mₙ。//一组连续值构成的服务器配置方案
3： ε ← 一个极小量；lb_φ, φ ← Find_lb_φ(n, λ₁, · · ·, λₙ, s, r̄)；C̄ ← 0；//初始化参数
4：while C̄ < C̃：//通过不断倍增自身直到系统单位成本超过给定的成本约束，寻找 φ的上界
5：φ ← φ / 2；//由于φ < 0，倍增操作实际上是除以2。
6：for i in range(n)：
7：mᵢ ← Find_mi_，满足_φ(λᵢ, s, r̄, φ)；
8：end for
9：C̄ ← idle ? 公式(14)计算的值 : 公式(15)计算的值；
10：end while
11：ub_φ ← φ；
12：while ub_φ − lb_φ > ε：//通过二分法算法在区间[lb_φ,ub_φ]内搜索φ
13：mid ← (lb_φ + ub_φ) / 2；
14： for i in range(n)：//根据新的φ值（即 mid）获取服务器配置方案
15：mᵢ ← Find_mi_，满足_φ(λᵢ, s, r̄, mid)；
16：end for
17：C̄ ← idle ? 公式(14)计算的值 : 公式(15)计算的值；
18：if C̄ > C̃：
19：ub_φ ← mid；
20： else：
21：lb_φ ← mid；
22：end if
23：end while
24： φ ← (lb_φ + ub_φ) / 2；
25：for i in range(n)：//根据确定的φ获取服务器配置方案
26：mᵢ ← Find_mi_，满足_φ(λᵢ, s, r̄, φ)；
27：end for
28：return m₁, m₂, · · ·, mₙ。

算法4. 离散化_配置_并_计算_平均响应时间约束
1: 输入：m₁, m₂, · · ·, mₙ, C̃, n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P*, 空闲。
2: 输出：m₁, m₂, · · ·, mₙ。 //最终服务器配置方案
3: λ ← λ₁ + λ₂ + · · · + λₙ； //初始化参数
4: for i in range(n):
5: mᵢ ← ⌊mᵢ⌋；
6: end for
7: do: //获取最终配置
8: mᵢ ← Sort_by_Ti_desc(m₁, m₂, · · ·, mₙ)[0]； // Ti的值由公式(A7)计算
9: mᵢ ← mᵢ + 1；
10: C̄ ← 空闲 ? 由公式(14)计算的值 : 由公式(15)计算的值；
11: while C̄ < C̃ //增加处理器数量直到系统单位成本超过给定的成本约束
12: T̄ ← (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + · · · + (λₙ / λ) Tₙ； //Ti的值由公式(A7)计算
13: return m₁, m₂, · · ·, mₙ, 和 T̄。

算法2描述了如何根据 φ，通过二分法算法（第7‐15行）寻找mᵢ以确定Sᵢ（即Sᵢ的处理器数量）的详细过程。在该算法中，我们通过lbi计算得到lbi = ⌈λᵢr/s⌉（第3行），并通过不断加倍自身直到满足φ(ubᵢ) > φ来获得ubᵢ（第4‐6行）。

关于如何在给定成本约束下找到优化性能的服务器配置方案的细节在算法3中进行了描述。第3至11行描述了寻找φ的下界和上界的过程。我们通过将自身不断加倍直到ub_φ使得C̄ > C̃满足条件（即，通过将自身不断加倍直到系统单位成本超过给定的成本约束，从而获得 φ的上界）。该算法使用二分法算法在区间[lb_φ, ub_φ]内搜索（第12至24行），并通过第25至28行获得处理器配置。需要注意的是，第9行和第17行中的条件运算符“？”根据idle的值计算系统单位成本，因为处理器在两种不同的工作模型下的能耗不同。当idle为真时，处理器工作模型支持空闲速度模型，否则仅支持恒定速度模型。

请注意，算法3的输出是一组连续值，即一组小数值。这样的结果在应用环境中是无法实现的。因此，我们提供了算法4以进一步离散化配置。该算法的基本思想是先对m₁, m₂, …, mₙ进行向下取整（第4–6行，这将降低成本但会增加响应时间），然后反复增加任务响应时间最长的边缘服务器上的处理器数量，直到C̄ > C̃满足条件（第7–11行）。Sort_by_Ti_desc(m₁, m₂, …, mₙ) 是一个排序函数（第8行），它根据mᵢ计算每个边缘服务器的任务响应时间Tᵢ，并按降序排列。

4.2 性能约束下的成本优化

在本节中，我们求解性能约束下的成本优化问题，即最小化成本
C̄ = Σᵢ₌₁ⁿ mᵢ ⋅ ((1+ω)cₚ / κ + cₑP ) + λr s^(α−1) cₑ,
对于空闲速度模型（表示处理器支持空闲速度模型时MEC系统的单位成本），以及
C̄ = Σᵢ₌₁ⁿ mᵢ ⋅ ((1+ω)cₚ / κ + (s^α + P ) cₑ),
对于恒定速度模型（表示处理器仅支持恒定速度模型时MEC系统的单位成本），需满足约束条件ρᵢ < 1（因为每个边缘服务器的负载不得超过其容量），对所有 1 ≤ i ≤ n，即mᵢ > λᵢx = λᵢr/s；以及T = T̃（表示系统性能必须接近给定的性能约束）。

为了促进推导，我们使用一个新函数 J(m₁, m₂, …, mₙ) 来表示 T = T̃，即
J(m₁, m₂, …, mₙ) = (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + … + (λₙ / λ) Tₙ - T̃.

我们还使用拉格朗日乘子法来求解此优化问题，我们有
∇C̄(m₁, m₂, …, mₙ) = η∇J(m₁, m₂, …, mₙ),
即，n个方程
∂C̄(m₁, m₂, …, mₙ) / ∂mᵢ = η ∂J(m₁, m₂, …, mₙ) / ∂mᵢ,
对于所有 1 ≤ i ≤ n，其中 η 是一个拉格朗日乘子。对 ∂C̄/∂mᵢ 求偏导数，我们得到
∂C̄ / ∂mᵢ = (1+ω)cₚ / κ + cₑP , (25)
对于空闲速度模型，以及
∂C̄ / ∂mᵢ = (1+ω)cₚ / κ + (s^α + P ) cₑ, (26)
对于恒定速度模型。对偏导数 ∂J/∂mᵢ 求导，我们得到
∂J / ∂mᵢ = (λᵢ / λ) ⋅ (∂Tᵢ / ∂mᵢ) = ∂T / ∂mᵢ. (27)

根据方程(20)、(25)、(26)和(27)，我们得到
((1+ω)cₚ / κ + cₑP ) / η = - (λᵢr / λs) ⋅ [√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1] / [mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²], (28)
对于空闲速度模型，以及
((1+ω)cₚ / κ + (s^α + P ) cₑ) / η = - (λᵢr / λs) ⋅ [√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1] / [mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²], (29)
对于恒定速度模型。请注意，方程(28)和(29)是mᵢ的函数。

让我们将公式(28)重写为
η = ((1+ω)cₚ / κ + cₑP ) ⋅ [- (λᵢr / λs) ⋅ (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1) / (mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²)]⁻¹, (30)
即，η_idle(mᵢ)。此外，公式(29)变为
η = ((1+ω)cₚ / κ + (s^α + P ) cₑ) ⋅ [- (λᵢr / λs) ⋅ (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) (ρᵢ + 3/2 - mᵢ(1−ρᵢ) ln ρᵢ) + 1) / (mᵢ² (1−ρᵢ)² (√(2πmᵢ(1−ρᵢ)) (eρᵢ / e^(ρᵢ))^(mᵢ) + 1)²)]⁻¹, (31)
即，η_constant(mᵢ)。根据我们在第4.1节中的分析，显然 η_idle(mᵢ)和 η_constant(mᵢ)是mᵢ的减函数。

类似地，我们使用二分法算法在一定范围内搜索 η和mᵢ以获得数值解。由于mᵢ的下界是
lbᵢ = ⌈λᵢr/s⌉,
我们得到 η的上界是
ub_η = { η_idle(lb_max), the idle-speed model; η_constant(lb_max), the constant-speed model;}
其中 lb_max = max₁≤ᵢ≤ₙ (lbᵢ).

通过不断将ub_η减半，直到T < T̃，即可获得 η的下界（即，lb_η），因为T是mᵢ的递减函数。

综上所述，给定n、λᵢ、s、r、cₚ、cₑ、ω、P*以及 T̃，我们用于寻找最优处理器配置m₁, m₂、…、mₙ以在满足性能约束 T̃的前提下最小化系统单位成本的算法可由算法5–8描述。

算法5. 查找 ub_η
1: 输入：n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P*, 空闲。
2: 输出：ub_η。
3: ub_η, lb_max ← 0； λ ← λ₁ + λ₂ + · · · + λₙ；//初始化参数
4: for i in range(n)：//查找所有 1 ≤ i ≤ n中lbᵢ的最大值
5: lbᵢ ← ⌈λᵢr̄/s⌉；
6: if lbᵢ > lb_max：
7: lb_max ← lbᵢ；
8: end if
9: end for
10: // η_idle(lb_max)和 η_constant(lb_max)的值分别由公式(30)和(31)计算得出，其中mᵢ ← lb_max
11: ub_η ← 空闲 ? η_idle(lb_max) : η_constant(lb_max)；
12: return ub_η。// 返回 η的上界

算法6. Find mi with η
1：输入： λᵢ, s, r̄, cₚ, cₑ, ω, P*, η, 空闲。
2：输出：mᵢ。
3： ε ← 一个非常小的量；lbᵢ, ubᵢ ← ⌈λᵢr̄/s⌉ //初始化 ε, lbᵢ, 和 ubᵢ
4：do:
5：ubi ← 2ubi；
6：// η_idle(ubi)和 η_constant(ubi)的值分别由公式(30)和(31)计算得到，其中 mᵢ ← ubi
7：η_cal ← 空闲 ? η_idle(ubi) : η_constant(ubi)
8：while η_cal > η //通过将自身翻倍，直到计算出的 η值小于给定值，从而找到mᵢ的上界
9：while ubᵢ − lbᵢ > ε：//通过二分法算法在[lbᵢ,ubi]范围内搜索mᵢ
10：mid ← (lbᵢ + ubᵢ) / 2；
11：// η_idle(mid)和 η_constant(mid)的值分别由公式(30)和(31)计算得到，其中mᵢ ← mid
12：η_cal ← 空闲 ? η_idle(mid) : η_constant(mid)
13：if η_cal > η：
14：lbᵢ ← mid；
15：else：
16：ubi ← mid；
17：end if
18：end while
19：mᵢ ← (lbᵢ + ubᵢ) / 2；
20：return mᵢ。//当给定 η时，返回Sᵢ的处理器数量

Sort_by_Ti(m₁, m₂, …, mₙ) 也是一个排序函数（第8行），用于根据mᵢ计算每个边缘服务器的任务响应时间，并按升序排序。Sort_by_Ti(m₁, m₂, …, mₙ)[0]表示取排序后的第一个元素，即获取每周期性能最佳的边缘服务器，并将其处理器数量减少一个（第8–9行）。

4.3 处理器选择

在本节中，我们将这两个问题扩展到服务提供商在构建MEC系统之前可以从不同硬件供应商提供的多种类型处理器中进行选择的情况，即每种处理器类型具有不同的速度、价格和基础功耗。我们给出了算法9来解决该问题。

设x表示可选的处理器类型数量。然后，我们使用s₁, s₂, …, sₓ; cₚ₁, cₚ₂, …, cₚₓ; 以及 P ₁, P ₂, …, P*ₓ; 分别表示不同类型处理器的速度、价格和基础功耗。我们算法的框架可描述如下：
- 首先，对于每种类型的处理器，我们可以使用性能约束成本优化算法或成本约束性能优化算法来获得一个最优的处理器配置方案；
- 其次，对于每种处理器的最优配置，我们可以相应地计算系统的平均任务响应时间和系统单位成本；
- 最后，我们可以根据这些性能和成本指标，确定性能最高或单位成本最低的处理器类型。

具体而言，我们使用一个布尔值参数 op_performance 来控制算法输出，即当 op_performance 为 true 时，算法输出在给定成本约束下性能最优的处理器类型和配置；当 op_performance 为 false 时，算法输出在给定性能约束下成本最低的处理器类型和配置。Tᵢ 和 Cᵢ 分别表示使用第 i 种类型处理器后系统的平均任务响应时间和系统单位成本。表达式 Sort_Tᵢ (T₁, T₂, …, Tₓ)[0] 和 Sort_Cᵢ (C₁, C₂, …, Cₓ)[0] 表示对输入参数进行排序，并返回首个元素的索引。

算法7. 在_性能_约束下寻找_配置_
1: 输入： T̃, n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P , idle。 // idle 是一个布尔值，表示处理器的工作模型
2: 输出： m₁, m₂, · · ·, mₙ。 // 一组连续值构成的服务器配置方案
3: // 初始化参数
4: ε ← 一个很小的量；ub_η, η ← Find_ub_η(n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P , idle)；T̄ ← 一个很大的量；
5: while T̄ > T̃： // 通过将自身减半来寻找 η 的下界，直到系统性能满足性能约束
6: η ← 2η； // 由于 η < 0，减半操作实际上是乘以2。
7: for i in range(n)：
8: mᵢ ← Find_mi_with_η(λᵢ, s, r̄, cₚ, cₑ, ω, P , η, idle)；
9: end for
10: T̄ ← (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + · · · + (λₙ / λ) Tₙ； // Tᵢ 的值由公式(A7)计算得出
11: end while
12: lb_η ← η；
13: while ub_η − lb_η > ε： // 通过二分法算法在区间 [lb_η, ub_η] 内搜索 η
14: mid ← (lb_η + ub_η) / 2；
15: for i in range(n)： // 根据 η 的新值（即 mid）获取服务器配置方案
16: mᵢ ← Find_mi_with_η(λᵢ, s, r̄, cₚ, cₑ, ω, P , mid, idle)；
17: end for
18: T̄ ← (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + · · · + (λₙ / λ) Tₙ； // Tᵢ 的值由公式(A7)计算得出
19: if T̄ > T̃：
20: ub_η ← mid；
21: else：
22: lb_η ← mid；
23: end if
24: end while
25: η ← (lb_η + ub_η) / 2；
26: for i in range(n)： // 根据确定的 η 获取服务器配置方案
27: mᵢ ← Find_mi_with_η(λᵢ, s, r̄, cₚ, cₑ, ω, P*, η, idle)；
28: end for
29: return m₁, m₂, · · ·, mₙ。

算法8. 离散化 配置并计算 C̄
1: 输入: m₁, m₂, · · ·, mₙ, T̃, n, λ₁, λ₂, · · ·, λₙ, s, r̄, cₚ, cₑ, ω, P*, 空闲。
2: 输出: m₁, m₂, · · ·, mₙ。 //最终服务器配置方案
3: λ ← λ₁ + λ₂ + · · · + λₙ; //初始化参数
4: for i in range(n):
5: mᵢ ← ⌈mᵢ⌉;
6: end for
7: do: //获取最终配置
8: mᵢ ← Sort_by_Ti(m₁, m₂, · · ·, mₙ)[0]; //Ti的值由公式(A7)计算
9: mᵢ ← mᵢ − 1;
10: T̄ ← (λ₁ / λ) T₁ + (λ₂ / λ) T₂ + · · · + (λₙ / λ) Tₙ; //Ti的值由公式(A7)计算
11: while T̄ < T̃
12: C̄ ← 空闲 ? 由公式(14)计算的值 : 由公式(15)计算的值;
13: return m₁, m₂, · · ·, mₙ, 和 C̄。

算法9. 处理器_选择
1: 输入：
2: C̃系统单位成本, T̃平均响应时间约束, n, λ₁, λ₂, · · ·, λₙ, r̄, cₑ, ω, 空闲, op_性能, x, s₁, s₂, · · · sₓ, cₚ₁, cₚ₂, · · ·, cₚₓ, P ₁, P ₂, · · ·, P ₓ;
3: 输出：
4: 索引；//所选的处理器类型 (1 ≤ 索引 ≤ x)
5: m₁, m₂, · · ·, mₙ。// 选择处理器的服务器配置方案
6: λ ← λ₁ + λ₂ + · · · + λₙ; //初始化参数
7: for i in range(x):
8: if op_性能：
9: m₁, m₂, · · ·, mₙ ← 算法3；//输入 sᵢ, cₚᵢ, P ᵢ
10: m₁, m₂, · · ·, mₙ ← 算法4；//使用 sᵢ, cₚᵢ, P ᵢ
11: T̄ᵢ ← (λ₁ / λ) T̄₁ + (λ₂ / λ) T̄₂ + · · · + (λₙ / λ) T̄ₙ
12: else:
13: m₁, m₂, · · ·, mₙ ← 算法7；//包含 sᵢ, cₚᵢ, P ᵢ
14: m₁, m₂, · · ·, mₙ ← 算法8；//包含 sᵢ, cₚᵢ, P*ᵢ
15: C̄ᵢ ← 空