多边形问题

求多边形面积：（向量法）

题目大意：
一个机器人站在坐标系的原点，每一次可以沿平行于坐标轴方向走 1 个单位到下一个整点或者沿对角线方向走 sqrt(2)个单位到下一个顶点。给出一个步行序列，保证机器人最后回到原点，求其走的路线围成的多边形的面积。步行序列中的 2、4、6、8 分别表示向南、东、西、北走一格（东和北是 x y 轴的正方向），1、3、7、9 分别是东北、西北、东南和西南，5 只会在序列的最后一位出现，表示站在原地不动了。
输入：
第一行有一个整数 t，表示有 t 组测试数据。每一组测试数据有一行，包含一个长度小于等于 1000000 的字符串，字符串是由数字组成的，表示一个步行序列。
输出：
每一组测试数据输出一行，即围成的多边形面积。如果面积是整数，则输出一个整数，否则输出一位小数。
分析：
将三角形分解成以若干个小三角形。三角形的面积用向量计算；

#include<stdio.h>
#include<math.h>
#include<string.h>

#define MaxN 1000005
#define eps  1e-8

struct Point
{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;}
};

const int way[9][2] = {{-1,-1},{0,-1},{1,-1},{-1,0},{0,0},{1,0},{-1,1},{0,1},{1,1}};

typedef Point Vector;

Vector operator - (Point a,Point b)
{
    return Vector(a.x-b.x,a.y-b.y);
}

//采用eps的精度判断大/小于零
int epssgn(double x)
{
    if (fabs(x)<eps) return 0;
    else return x<0?-1:1;
}

/* 2向量求叉积，同时也可以求面积 */
double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

int main()
{
    int t,n,i,len;
    char c,str[MaxN];
    double res;
    long long ans;
    Point p0(0,0),p1,p2;
    freopen("poj1654.txt","r",stdin);
    freopen("poj1654ans.txt","w",stdout);
    scanf("%d",&t);
    while (t--)
    {
        scanf("%c%s",&c,str);
        len=strlen(str);
        if (len<=3)
        {
            printf("0\n");
            continue;
        }
        p1.x=p0.x+way[str[0]-'1'][0];
        p1.y=p0.y+way[str[0]-'1'][1];
        res=0;
        for (i=1;i<len-1;i++)
        {
            p2.x=p1.x+way[str[i]-'1'][0];
            p2.y=p1.y+way[str[i]-'1'][1];
            res+=Cross(p1,p2);
            p1=p2;
        }
        getchar();
        if (epssgn(res)<0) res=-res;
        ans=(long long )res;
        if (ans&1) printf("%lld.5\n",ans/2);
        else printf("%lld\n",ans/2);
    }
    return 0;
}

POJ1408【基础】
题目大意：
有一个 1×1 的正方形，左下角在原点，两条边和坐标轴正半轴重合。每条边上有 n 个点（不包括顶点，1<=n<=30），上下边上的点按序号对应连线后不会互相交叉，左右边上的点也是如此。这些连线将正方形分隔成(n-1)*(n-1)个四边形。求最大的四边形的面积。
输入：
有若干组测试数据。每一组测试数据第一行有一个整数 n，当 n=0 时测试数据结束。接下来有四行，每一行有 n 个小数，分别是下、上、左、右边上的点对应的坐标（上下边对应 x 坐标，左右边对应 y 坐标）。
输出：
每一组测试数据输出一行，包含一个整数，即最大的小四边形的面积。

题解：
依次求出各线的交点后枚举每一个小四边形求其面积。为了统一化处理，将正方形四个顶点也加入到交点集中。然后求多边形面积。

#include<cstdio>
#include<cmath>

using namespace std;

#define eps 1e-8
#define INF 1e20
#define MaxN 35
#define max(a,b) (a)>(b)?(a):(b)

struct Point
{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;} 
};

typedef Point Vector;

struct Line //ax+by+c=0 
{
    double a,b,c;
    Line(Point &p1,Point &p2)
    {
        a=p1.y-p2.y;
        b=p2.x-p1.x;
        c=p1.x*p2.y-p2.x*p1.y;
    }
    Line(){}
};

Point GetIntersect(Line &l1, Line &l2) //取交点 
{
    Point res;
    res.x=(l1.b*l2.c-l2.b*l1.c)/(l1.a*l2.b-l2.a*l1.b);
    res.y=(l1.c*l2.a-l2.c*l1.a)/(l1.a*l2.b-l2.a*l1.b);
    return res;
}

Vector operator - (Point a,Point b)    
{
    return Vector(a.x-b.x,a.y-b.y);
}

/* 2向量求叉积*/
double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

/*求多边形面积，要求点集按逆时针顺序*/
double ConvexPolygonArea(Point * p,int n)
{
    double area=0;
    int i;
    for (i=1;i<n-1;i++) area+=Cross(p[i]-p[0],p[i+1]-p[0]);
    return area/2;
}

int n;
Point map[MaxN][MaxN];
double p[4][MaxN];

void BuildMap()
{
    int i,j;
    for (i=0;i<=n+1;i++)
    {
        Point p1(0,p[2][i]),p2(1,p[3][i]);
        Line l1(p1,p2); //横边
        for (j=0;j<=n+1;j++)
        {
            p1=Point(p[0][j],0);
            p2=Point(p[1][j],1);
            Line l2(p1,p2);  //纵边
            map[i][j]=GetIntersect(l1,l2); //取交点。 
        }
    }
}

int main()
{
    int i,j;
    double area,ans;
    Point rect[4];
    freopen("poj1408.txt","r",stdin);
    freopen("poj1408ans.txt","w",stdout);
    while (scanf("%d",&n) && n)
    {
        for (i=0;i<4;i++)//0-3分别代表不同的边 
        {
                   p[i][0]=0;  //把正方形四条边加进去
            	   p[i][n+1]=1;
                   for (j=1;j<=n;j++) scanf("%lf",&p[i][j]);
        }
        BuildMap();
        ans=0;
        for (i=0;i<=n;i++)
            for (j=0;j<=n;j++)
            {
                       rect[0]=map[i][j];
                       rect[1]=map[i][j+1];
                       rect[2]=map[i+1][j+1];
                       rect[3]=map[i+1][j];
                       area=ConvexPolygonArea(rect,4);
                       ans=max(area,ans);
            }
        printf("%.6f\n",ans);
    }
    return 0;
} 

求多边形的边覆盖的整点数，和内部整点数以及面积。

pick定理：设Γ 为平面上以格子点为顶点之单纯多边形，则其面积为

其中b为边界上的格子点数，i为内部的格子点数。

POJ1265【基础】
题目大意：
有一个机器人，一开始在(0,0)点，每一次一定会走去一个整数坐标格点，最后走回原点，路径围成一个多边形。这些点是逆时针排布的。求：1、多边形的边覆盖的整点数有多少个；2、这个多边形内部的整数坐标格点有多少个；3、这个多边形的面积是多少。
输入：
第一行有一个整数 t，表示有 t 组测试数据。每一组测试数据第一行有一个整数 n，表示多边形有 n 个点。接下来有 n 行，每一行有两个整数，表示下一个点与当前点的 xy 坐标的差(dx,dy)。
输出：
每一组测试数据先输出一行“Scenario #%d:”，%d 表示当前测试数据组编号。接下来输出一行，包含；两个整数即多边形内部的整点数和多边形边上的整点数，以及一个一位小数，即多边形的面积。

分析：
多边形边上经过的整点数等于x y 改变值绝对值的最大公约数。面积可以通过叉乘计算到，

#include<stdio.h>
#include<math.h>

#define MaxN 101

struct Point
{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;}
};

typedef Point Vector;

Vector operator - (Point a,Point b)
{
    return Vector(a.x-b.x,a.y-b.y);
}

/* 2向量求叉积，同时也可以求面积 */
double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

int gcd(int a,int b)
{
    return b>0?gcd(b,a%b):a;
}

int iabs(int x)   //fabs()绝对值函数； 
{
    if (x>0) return x; else return -x;
}

Point p[MaxN];

int main()
{
    int n,i,k,t,e,dx,dy;
    double s;
    freopen("poj1265.txt","r",stdin);
    freopen("poj1265ans.txt","w",stdout);
    scanf("%d",&t);
    for (k=1;k<=t;k++)
    {
        scanf("%d",&n);
        p[0]=Point(0,0);
        e=0;s=0;
        for (i=1;i<=n;i++)
        {
            scanf("%d%d",&dx,&dy);
            p[i].x=p[i-1].x+dx;
            p[i].y=p[i-1].y+dy;
            s+=Cross(p[i-1],p[i]); //注意前后顺序，会影响符号
            if (dx==0 || dy==0) e+=iabs(dx+dy);
            else e+=gcd(iabs(dx),iabs(dy));  //画个图就知道最大公约数是连线上的整点
        }
        s=fabs(s)/2;  //面积注意要除2，因为叉乘直接得到的是平行四边形面积
        i=(int)(s+1-e/2);
        printf("Scenario #%d:\n",k);
        printf("%d %d %.1f\n\n",i,e,s);
    }
    return 0;
}

求多边形的重心：

重心
1质量集中在顶点上。n 个顶点坐标为(xi,yi)，质量为 mi，则重心

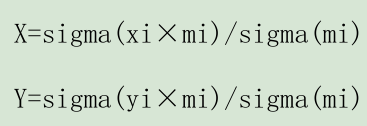
sigma----求和；
特殊地，若每个点的质量相同，则
X=sigma(xi)/n
Y=sigma(yi)/n

2质量分布均匀。
三角形：
X=(x0+x1+x2)/3
Y=(y0+y1+y2)/3

面对多边形时，以第一个顶点为基准，分别连接 p[i]、p[i+1]，1<i<n，则可将多边形划分为若干个三角形。求出每个三角形的重心和质量，可以构造一个新的多边形，顶点为所有三角形的重心，顶点质量为三角形的质量，然后转化为情况 1。

POJ1385【基础】
题目大意：
给出一个多边形的各顶点，求这个多边形的重心。
输入：
第一行有一个整数 t，表示有 t 组测试数据。每一组测试数据第一行有一个整数 n，表示有 n 个点（1<=n<=1000000）。接下来有 n 行每一行有两个整数，表示一个顶点的坐标（绝对值小于 20000），顶点是按逆时针顺序给出的。
输出：
每一组测试数据输出一行，包含空格隔开的 两个两位小数，即重心的 xy 坐标。

#include<stdio.h>
#include<math.h>

struct Point
{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;}
};

typedef Point Vector;

Vector operator - (Point &a,Point &b)
{
    return Vector(a.x-b.x,a.y-b.y);
}

/* 2向量求叉积，同时也可以求面积 */
double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

Point BaryCenter(int n,Point *p)
{
    Point res(0,0);
    double s=0.0,t;
    int i;
    for (i=1;i<n-1;i++)
    {
        t=Cross(p[i]-p[0],p[i+1]-p[0])/2;   //分割成三角形，算面积
        s+=t;
        res.x+=(p[0].x+p[i].x+p[i+1].x)*t;  //将面积作为重量放在每一个小三角形的重心上,就将pdf中的第二种情况转换为第一种情况， 
        res.y+=(p[0].y+p[i].y+p[i+1].y)*t;  //质量*坐标，三角形重心所需的除以3放在后面
    }
    res.x/=(3*s);
    res.y/=(3*s);
    return res;
}

int main()
{
    int t,n,i;
    Point ans,*p;
    freopen("poj1385.txt","r",stdin);
    freopen("poj1385ans.txt","w",stdout);
    scanf("%d",&t);
    while (t--)
    {
        scanf("%d",&n);
        p=new Point[n];
        for (i=0;i<n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
        ans=BaryCenter(n,p);
        printf("%.2f %.2f\n",ans.x,ans.y);
        delete []p;
    }
    return 0;
}

求多边形与圆的重叠面积。

思考：POJ 3675

这里给出一个简单的模板例子：

题目大意：
给出一个三角形的三个顶点坐标和圆的圆心及半径，求三角形与圆重叠的面积。
输入：
有若干组测试数据，每一组测试数据有一行。前三对空格分隔的小数表示一个三角形的三个点的 x y 坐标，第四对空格分隔的小数表示圆心的 x y 坐标，最后一个小数表示园的半径。
输出：
每一组测试数据输出一行， 即一个两位小数，表示重叠的面积。

#include<stdio.h>
#include<math.h>

#define eps  1e-8
#define pi   3.141592653589793
#define MaxN 5

struct Point
{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;}
};

typedef Point Vector;

Vector operator + (Point &a,Point &b)
{
    return Vector(a.x+b.x,a.y+b.y);
}

Vector operator - (Point &a,Point &b)
{
    return Vector(a.x-b.x,a.y-b.y);
}

//2向量求叉积
double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

double Dot(Vector a,Vector b)
{
    return a.x*b.x+a.y*b.y;
}

//采用eps的精度判断大/小于零
int epssgn(double x)
{
    if (fabs(x)<eps) return 0;
    else return x<0?-1:1;
}

double len(Point a)
{
    return sqrt(a.x*a.x+a.y*a.y);
}

Point res[MaxN];
double r;

double min(double a,double b)
{
    return a<b?a:b;
}

//红书《算法与实现》的模板，求扇形面积
double SectorArea(Point &a,Point &b)
{
    double theta=atan2(a.y,a.x)-atan2(b.y,b.x);
    while (theta<=0) theta+=2*pi;
    while (theta>=2*pi) theta-=2*pi;
    theta=min(theta,2*pi-theta);
    return r*r*theta/2;
}

//红书《算法与实现》的模板，求园与线段（直线）的交点
void CircleCrossLine(Point a,Point b,Point o,double r,Point ret[],int &num)
{
    double x0=o.x,y0=o.y;
    double x1=a.x,y1=a.y;
    double x2=b.x,y2=b.y;
    double dx=x2-x1,dy=y2-y1;
    double A=dx*dx+dy*dy;
    double B=2*dx*(x1-x0)+2*dy*(y1-y0);
    double C=(x1-x0)*(x1-x0)+(y1-y0)*(y1-y0)-r*r;
    double delta=B*B-4*A*C;
    num=0;
    if (epssgn(delta)>=0)
    {
        double t1=(-B-sqrt(fabs(delta)))/(2*A);
        double t2=(-B+sqrt(fabs(delta)))/(2*A);
        if (epssgn(t1-1.0)<=0 && epssgn(t1)>=0)
            ret[num++]=Point(x1+t1*dx,y1+t1*dy);
        if (epssgn(t2-1.0)<=0 && epssgn(t2)>=0)
            ret[num++]=Point(x1+t2*dx,y1+t2*dy);
    }
}

double Calc(Point &a,Point &b)  //红书模板
{
    Point p[2];
    int num=0;
    int ina=(epssgn(len(a)-r)<0);
    int inb=(epssgn(len(b)-r)<0);
    if (ina)
    {
        if (inb) return fabs(Cross(a,b))/2.0; //情形1
        else  //情形2
        {
            CircleCrossLine(a,b,Point(0,0),r,p,num);
            return SectorArea(b,p[0])+fabs(Cross(a,p[0]))/2.0;
        }
    }
    else
    {
       CircleCrossLine(a,b,Point(0,0),r,p,num);
        if (inb) return SectorArea(p[0],a)+fabs(Cross(p[0],b))/2.0; //情形2
        else
        {
            if (num==2) return SectorArea(a,p[0])+SectorArea(p[1],b)+fabs(Cross(p[0],p[1]))/2.0; //情形4
            else return SectorArea(a,b);  //情形3
        }
    }
}

int main()
{
    int i,n,sgn;
    double ans,x0,y0;
    freopen("poj2986.txt","r",stdin);
    freopen("poj2986ans.txt","w",stdout);
    while (scanf("%lf%lf",&res[0].x,&res[0].y)!=EOF)
    {
        for (i=1;i<3;i++) scanf("%lf%lf",&res[i].x,&res[i].y);
        scanf("%lf%lf",&x0,&y0);
        for (i=0;i<3;i++)
        {
            res[i].x-=x0;
            res[i].y-=y0;
        }
        scanf("%lf",&r);
        res[3]=res[0];
        ans=0;
        for (i=0;i<3;i++)
        {
            sgn=epssgn(Cross(res[i],res[i+1]));
            if (sgn!=0) ans+=sgn*Calc(res[i],res[i+1]);
        }
        printf("%.2f\n",fabs(ans));
    }
    return 0;
}