三次样条插值Python实现

函数

$$y=\frac{1}{1+x^2}$$

算法分析

三次样条插值。就是在分段插值的一种情况。
要求：

• 在每个分段区间上是三次多项式（这就是三次样条中的三次的来源）
• 在整个区间（开区间）上二阶导数连续（当然啦，这里主要是强调在节点上的连续）
• 加上边界条件。边界条件只需要给出两个方程。构建一个方程组，就可以解出所有的参数。

这里话，根据第一类样条作为边界。（就是知道两端节点的导数数值，然后来做三次样条插值）

但是这里也分为两种情况，分别是这个数值是随便给的一个数，还是说根据函数的在对应点上数值给出。

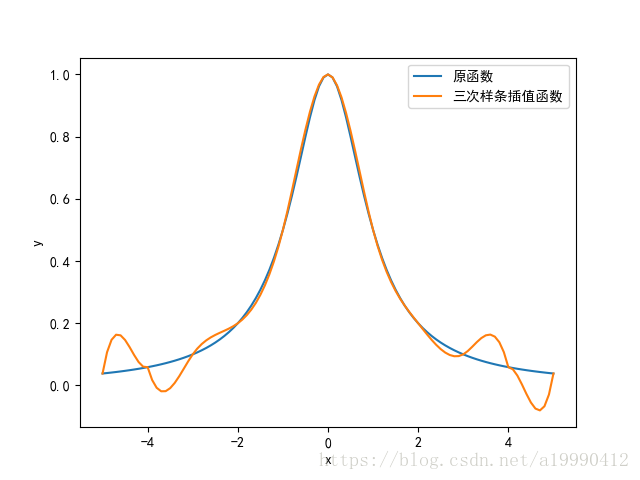
情况一：两边导数数值给出

这里假设数值均为1。即 $f^{\prime }(x_0)=f^{\prime }(x_n)=1$的情况。

情况一图像

情况一代码

import numpy as np
from sympy import *
import matplotlib.pyplot as plt


def f(x):
    return 1 / (1 + x ** 2)


def cal(begin, end, i):
    by = f(begin)
    ey = f(end)
    I = Ms[i] * ((end - n) ** 3) / 6 + Ms[i + 1] * ((n - begin) ** 3) / 6 + (by - Ms[i] / 6) * (end - n) + (
            ey - Ms[i + 1] / 6) * (n - begin)
    return I


def ff(x):  # f[x0, x1, ..., xk]
    ans = 0
    for i in range(len(x)):
        temp = 1
        for j in range(len(x)):
            if i != j:
                temp *= (x[i] - x[j])
        ans += f(x[i]) / temp
    return ans


def calM():
    lam = [1] + [1 / 2] * 9
    miu = [1 / 2] * 9 + [1]
    # Y = 1 / (1 + n ** 2)
    # df = diff(Y, n)
    x = np.array(range(11)) - 5
    # ds = [6 * (ff(x[0:2]) - df.subs(n, x[0]))]
    ds = [6 * (ff(x[0:2]) - 1)]
    for i in range(9):
        ds.append(6 * ff(x[i: i + 3]))
    # ds.append(6 * (df.subs(n, x[10]) - ff(x[-2:])))
    ds.append(6 * (1 - ff(x[-2:])))
    Mat = np.eye(11, 11) * 2
    for i in range(11):
        if i == 0:
            Mat[i][1] = lam[i]
        elif i == 10:
            Mat[i][9] = miu[i - 1]
        else:
            Mat[i][i - 1] = miu[i - 1]
            Mat[i][i + 1] = lam[i]
    ds = np.mat(ds)
    Mat = np.mat(Mat)
    Ms = ds * Mat.I
    return Ms.tolist()[0]


def calnf(x):
    nf = []
    for i in range(len(x) - 1):
        nf.append(cal(x[i], x[i + 1], i))
    return nf


def calf(f, x):
    y = []
    for i in x:
        y.append(f.subs(n, i))
    return y


def nfSub(x, nf):
    tempx = np.array(range(11)) - 5
    dx = []
    for i in range(10):
        labelx = []
        for j in range(len(x)):
            if x[j] >= tempx[i] and x[j] < tempx[i + 1]:
                labelx.append(x[j])
            elif i == 9 and x[j] >= tempx[i] and x[j] <= tempx[i + 1]:
                labelx.append(x[j])
        dx = dx + calf(nf[i], labelx)
    return np.array(dx)


def draw(nf):
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    x = np.linspace(-5, 5, 101)
    y = f(x)
    Ly = nfSub(x, nf)
    plt.plot(x, y, label='原函数')
    plt.plot(x, Ly, label='三次样条插值函数')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()

    plt.savefig('1.png')
    plt.show()


def lossCal(nf):
    x = np.linspace(-5, 5, 101)
    y = f(x)
    Ly = nfSub(x, nf)
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print(temp.mean())


if __name__ == '__main__':
    x = np.array(range(11)) - 5
    y = f(x)

    n, m = symbols('n m')
    init_printing(use_unicode=True)
    Ms = calM()
    nf = calnf(x)
    draw(nf)
    lossCal(nf)

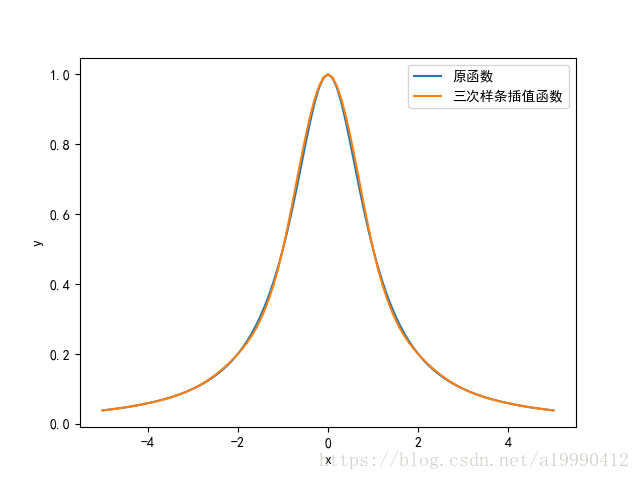
情况二：两边导数数值由函数本身算出

这里假设数值均为1。即 $f^{\prime }(x_i)=S^{\prime }(x_i)(i=0,n)$的情况。

情况二图像

情况二代码

import numpy as np
from sympy import *
import matplotlib.pyplot as plt


def f(x):
    return 1 / (1 + x ** 2)


def cal(begin, end, i):
    by = f(begin)
    ey = f(end)
    I = Ms[i] * ((end - n) ** 3) / 6 + Ms[i + 1] * ((n - begin) ** 3) / 6 + (by - Ms[i] / 6) * (end - n) + (
            ey - Ms[i + 1] / 6) * (n - begin)
    return I


def ff(x):  # f[x0, x1, ..., xk]
    ans = 0
    for i in range(len(x)):
        temp = 1
        for j in range(len(x)):
            if i != j:
                temp *= (x[i] - x[j])
        ans += f(x[i]) / temp
    return ans


def calM():
    lam = [1] + [1 / 2] * 9
    miu = [1 / 2] * 9 + [1]
    Y = 1 / (1 + n ** 2)
    df = diff(Y, n)
    x = np.array(range(11)) - 5
    ds = [6 * (ff(x[0:2]) - df.subs(n, x[0]))]
    # ds = [6 * (ff(x[0:2]) - 1)]
    for i in range(9):
        ds.append(6 * ff(x[i: i + 3]))
    ds.append(6 * (df.subs(n, x[10]) - ff(x[-2:])))
    # ds.append(6 * (1 - ff(x[-2:])))
    Mat = np.eye(11, 11) * 2
    for i in range(11):
        if i == 0:
            Mat[i][1] = lam[i]
        elif i == 10:
            Mat[i][9] = miu[i - 1]
        else:
            Mat[i][i - 1] = miu[i - 1]
            Mat[i][i + 1] = lam[i]
    ds = np.mat(ds)
    Mat = np.mat(Mat)
    Ms = ds * Mat.I
    return Ms.tolist()[0]


def calnf(x):
    nf = []
    for i in range(len(x) - 1):
        nf.append(cal(x[i], x[i + 1], i))
    return nf


def calf(f, x):
    y = []
    for i in x:
        y.append(f.subs(n, i))
    return y


def nfSub(x, nf):
    tempx = np.array(range(11)) - 5
    dx = []
    for i in range(10):
        labelx = []
        for j in range(len(x)):
            if x[j] >= tempx[i] and x[j] < tempx[i + 1]:
                labelx.append(x[j])
            elif i == 9 and x[j] >= tempx[i] and x[j] <= tempx[i + 1]:
                labelx.append(x[j])
        dx = dx + calf(nf[i], labelx)
    return np.array(dx)


def draw(nf):
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    x = np.linspace(-5, 5, 101)
    y = f(x)
    Ly = nfSub(x, nf)
    plt.plot(x, y, label='原函数')
    plt.plot(x, Ly, label='三次样条插值函数')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()

    plt.savefig('1.png')
    plt.show()


def lossCal(nf):
    x = np.linspace(-5, 5, 101)
    y = f(x)
    Ly = nfSub(x, nf)
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print(temp.mean())


if __name__ == '__main__':
    x = np.array(range(11)) - 5
    y = f(x)

    n, m = symbols('n m')
    init_printing(use_unicode=True)
    Ms = calM()
    nf = calnf(x)
    draw(nf)
    lossCal(nf)