悬架&天棚算法

原创已于 2025-12-17 14:53:12 修改 · 872 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #汽车

于 2025-12-15 17:27:01 首次发布

悬架

悬架的定义：
- 连接车轮与车身的**机构。支撑车身保持几何姿态+**缓冲路面冲击+传递车轮与路面间的力和力矩，保证轮胎抓地力，关乎操控稳定与安全
悬架设计的难点：“舒适性”与“操控性”的权衡
- 舒适性：需要“软”悬架，隔离路面振动
- 操控性：需要“硬”悬架，减少车身侧倾、俯仰，保持轮胎紧贴路面
  - 注释：软悬架（刚度低）软悬架能够更好地吸收高频振动，如路面接缝或不平引起的冲击。它通过降低共振频率，减少车身振动对乘客的影响，从而提升乘坐舒适性。然而，过于柔软的悬架可能导致低频振动（如长波路面）的持续时间更长，可能引起乘客的不适感。
  - 注释：硬悬架能够更快地抑制振动，减少车身的晃动，但在处理高频振动时可能不够柔和，导致更多的振动传递到车内，影响舒适性。
  - 软悬架的共振频率较低，能够更好地适应高频振动，减少乘客感受到的振动强度。而硬悬架的共振频率较高，可能与人体敏感的频率范围（4~8Hz）重叠，导致不适感。
  - 共振频率是指当一个系统受到外界周期性力的作用时，其固有频率与外界力的频率一致时所达到的频率。
  - 高频振动通常指的是频率较高的振动，一般在几百赫兹以上。高频振动传递到车内时，可能会产生尖锐的噪声，影响车内环境的安静性。人体对高频振动的敏感度较低，但过高的高频振动仍可能引起不适。低频振动指的是频率较低的振动，通常在几十赫兹以下。低频振动对人体的影响更为显著，尤其是对内脏和整体身体的晃动，可能导致疲劳和不适。人体对低频振动特别敏感，因此在汽车设计中，减少低频振动是提升乘坐舒适性的关键。
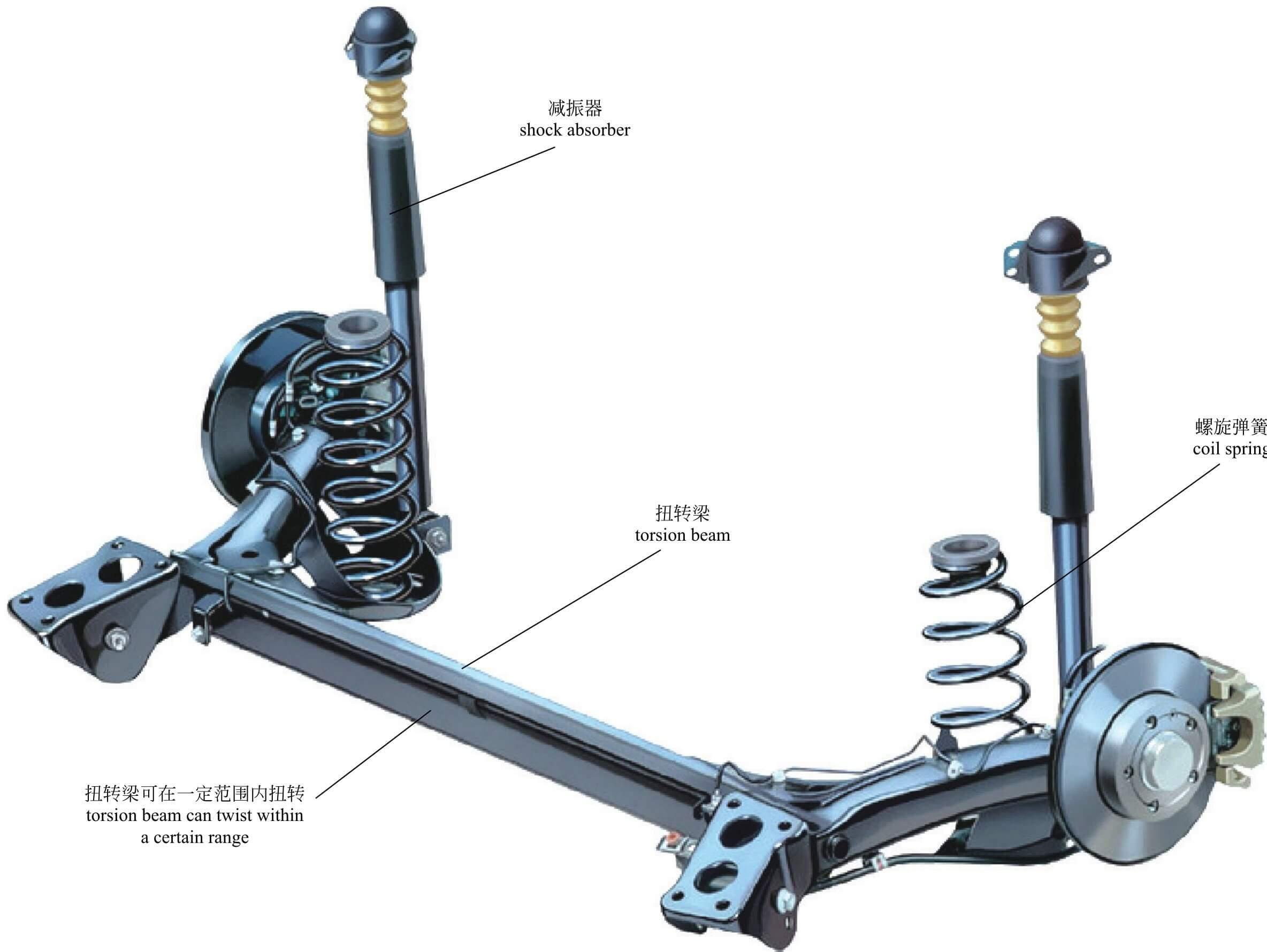
悬架的核心部件
- 弹性元件（弹簧）
  - 作用：支撑车身，储存/释放能量，决定悬架“软硬”基调
  - 关键参数：刚度K – 刚度越大抵抗变形的能力越强，车身姿态越稳，但过滤小振动能力越差
- 减震器
  - 作用：消耗弹簧储存的能量，抑制车身振荡。
  - 关键参数：阻尼系数
- 导向机构-连杆与摆臂
  - 作用：决定车轮跳动的轨迹（外倾角、前束角等变化规律）
关键状态量与性能指标
- 簧载质量：车身
- 非簧载质量：车轮、制动系统等
- 悬架行程：车轮与车身的相对位移。防止“打顶”（撞到上限位块）和“托底”（撞到下限位块）是控制的基本约束
- 车身姿态：俯仰角pitch、侧倾角roll、垂向加速度heave
- 轮胎动载荷：轮胎与地面间垂直方向的动态力
悬架的分类
- **被动悬架：**弹簧（刚度K固定）和减振器（阻尼C固定）的参数在车辆出厂后无法改变
- **半主动悬架：**阻尼系数（C）可以实时主动调节，但弹簧刚度（K）依然固定。系统不能向车身注入能量，主流的技术方案是：
  - CDC（连续阻尼控制）减振器：通过电磁阀改变油液通路孔径，实现阻尼无级调节
  - MR（磁流变）减振器：通过改变磁场，使内部的磁流变液粘度瞬间变化，从而改变阻尼
- 空气悬架：
  - 使用空气弹簧（内部是压缩空气）替代传统的金属螺旋弹簧。通常需要与可调阻尼减振器（如CDC）结合使用。
  - 可调刚度：通过充放气改变空气弹簧内的气压，从而改变其等效刚度。气压高则硬，气压低则软。
  - 可调车高：通过整体充放气，改变悬架行程的初始位置，实现车身的升高或降低。
- **主动悬架：**配备独立的力作动器（如液压、电磁）能向系统注入能量，理论上能完全控制车身运动
  - 可以做到在刹车时主动抵抗“点头”，转弯时主动抵抗“侧倾”，过坎时主动抬起车轮抵消冲击。性能天花板是所有悬架中最高的。
整车平顺性的7自由度模型：
- 车身的垂直heave、俯仰pitch、侧倾roll
- 4个车轮有4个垂直度的自由度

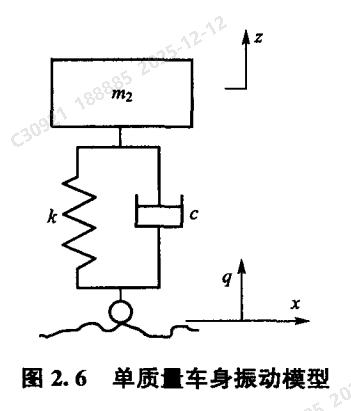
单质量车身微分振动方程

公式：
- $m_2 d2 zdt2 + c ( dzdt − dqdt ) + k(z − q) = 0m\_{2} \frac{d^2 z}{dt^2} + c \left( \frac{dz}{dt} - \frac{dq}{dt} \right) + k(z - q) = 0$ → $m_2 d2 zdt2 + c dzdt + kz = c dqdt + kqm\_{2} \frac{d^2 z}{dt^2} + c \frac{dz}{dt} + kz = c \frac{dq}{dt} + kq$
- $m_2 z¨ + c(z˙ − q˙) + k(z − q) = 0m\_2 \ddot{z} + c(\dot{z} - \dot{q}) + k(z - q) = 0$ → $m_2 z¨ + c z˙ + kz = c q˙ + kqm\_2 \ddot{z} + c \dot{z} + kz = c \dot{q} + kq$
  - $m\_{2}$ ：簧上质量（Kg）-由悬架支撑的车身部分的质量。在单质量模型中，它代表分配到该悬架上的车身质量（如1/4车身质量）
  - $z ：$ 车身垂直位移（m）-车身质量块相对于静止平衡位置的垂直位移（绝对位移），通常以向上为正方向
  - $c$ ：悬架阻尼系数(N·m/s)：减振器的阻尼特性。阻尼越大，振动衰减越快，但过大会导致悬架变硬
  - $k$ ：悬架弹簧刚度(N/m)：悬架弹簧的软硬程度。刚度越大，产生单位变形所需的力越大，悬架越“硬”
  - $q$ ：路面相对于理想平滑路面的垂直位移（绝对位移）。是系统的主要激励源，通常以向上为正
  - $z¨\ddot{z}$ ：车身加速度
  - $q˙\dot{q}$ ：路面的相对速度
示意图
公式推导：
- $m_2 z¨m\_2 \ddot{z}$ ：质量 × 加速度 = 惯性力（牛顿第二定律 F=ma）
- $- k (z - q)$ ：弹簧力
- $- c (z - q)$ ：阻尼力与相对速度有关
举例子：
- 时间点1：车轮刚要上凸起
路面 q 开始上升，车身 z 还没动

z - q 变小 → 弹簧被压缩 → 弹簧力向上（推车身）

dz/dt - dq/dt 为负（路面向上比车身快）→ 阻尼力向上
- 时间点2：车轮在凸起顶端
路面 q 开始下降，车身 z 被弹簧推着还在向上

z - q 变大 → 弹簧被拉伸 → 弹簧力向下（拉车身）

dz/dt - dq/dt 为正（车身向上比路面快）→ 阻尼力向下
- 整个过程中，弹簧和阻尼器共同作用，消耗能量，让车身振动尽快平息。
代码模拟

import numpy as np
import matplotlib.pyplot as plt

# 参数
m = 300  # kg
k = 20000  # N/m
c = 2000  # N·s/m

# 时间设置
dt = 0.001  # 时间步长
t = np.arange(0, 5, dt)  # 5秒

# 路面激励：一个简单的凸起
q = np.zeros_like(t)
q[(t >= 1) & (t <= 1.2)] = 0.05 * np.sin(np.pi*(t[(t >= 1) & (t <= 1.2)]-1)/0.2)

# 初始化
z = np.zeros_like(t)  # 车身位移
dz = np.zeros_like(t)  # 车身速度

# 数值积分（欧拉法）
for i in range(1, len(t)):
    # 计算加速度
    ddz = (-k*(z[i-1] - q[i-1]) - c*(dz[i-1] - (q[i]-q[i-1])/dt)) / m
    
    # 更新速度和位移
    dz[i] = dz[i-1] + ddz * dt
    z[i] = z[i-1] + dz[i] * dt

# 绘图
plt.figure(figsize=(12, 8))

plt.subplot(3, 1, 1)
plt.plot(t, q, label='路面位移 q(t)')
plt.ylabel('位移 (m)')
plt.legend()
plt.title('路面激励与车身响应')

plt.subplot(3, 1, 2)
plt.plot(t, z, label='车身位移 z(t)', color='orange')
plt.ylabel('位移 (m)')
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(t, dz, label='车身速度 dz/dt', color='green')
plt.xlabel('时间 (s)')
plt.ylabel('速度 (m/s)')
plt.legend()

plt.tight_layout()
plt.show()

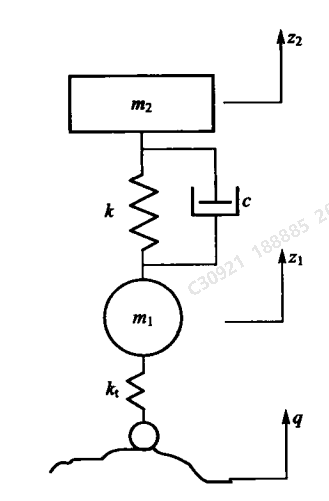
双质量系统振动微分方程–二自由度的1/4车辆模型

公式： $m_2 z¨_2 + c(z˙_2 − z˙_1) + k(z_2 − z_1) = 0 m_1 z¨_1 + c(z˙_1 − z˙_2) + k(z_1 − z_2) + k_t(z_1 − q) = 0m\_2 \ddot{z}\_2 + c(\dot{z}\_2 - \dot{z}\_1) + k(z\_2 - z\_1) = 0 \\ m\_1 \ddot{z}\_1 + c(\dot{z}\_1 - \dot{z}\_2) + k(z\_1 - z\_2) + k\_t(z\_1 - q) = 0$
- 公式矩阵化：
  - $F_q\mathbf{M} \ddot{\mathbf{Z}} + \mathbf{C} \dot{\mathbf{Z}} + \mathbf{K} \mathbf{Z} = \mathbf{F}\_q$
    - 位移向量： $KaTeX parse error: Undefined control sequence: \[ at position 14: \mathbf{Z} = \̲[̲z\_2, z\_1\]^T$
    - 质量矩阵： $m_2 0 0 m_1 ]\mathbf{M} = \begin{bmatrix} m\_2 & 0 \\ 0 & m\_1 \end{bmatrix}$
    - 阻尼刚度： $]\mathbf{C} = \begin{bmatrix} c & -c \\ -c & c \end{bmatrix}$
    - 刚度矩阵： $k_t ]\mathbf{K} = \begin{bmatrix} k & -k \\ -k & k + k\_t \end{bmatrix}$
    - 输入向量： $F_q = [ 0 k_t q ]\mathbf{F}\_q = \begin{bmatrix} 0 \\ k\_t q \end{bmatrix}$
- $m\_2$ ：簧上质量（悬挂质量）–包括车身、负载等由悬架支撑的质量
- $z\_2$ ：簧上质量的垂直位移，绝对坐标，向上为正
- $m\_1$ ：簧下质量（非悬挂质量）-- 包括车轮、车轴、制动盘等随车轮跳动的质量
- $z\_1$ ：簧下质量的垂直位移，绝对坐标，向上为正
- $q$ ：路面不平度位移，，绝对坐标，向上为正，是系统的输入激励
- $c$ ：悬架阻尼系数(N·m/s)：减振器的阻尼特性。阻尼越大，振动衰减越快，但过大会导致悬架变硬
- $k$ ：悬架弹簧刚度(N/m)：悬架弹簧的软硬程度。刚度越大，产生单位变形所需的力越大，悬架越“硬”
- $k\_{1}$ ：轮胎垂直刚度(N/m)
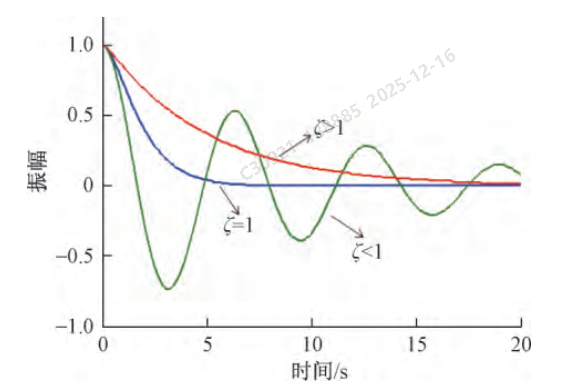
固有频率与阻尼比
- 固有频率：汽车过坎后，车身会上下振动，这个振动的频率就是悬架系统的固有频率。对于轿车，这个频率大约为 1-1.5 Hz（每秒振动1-1.5次）
- 阻尼比：过坎后，车身振动衰减的速度，阻尼比越大，振动停得越快。车身是低频，车轮是高频
  - $f_wheel ≈ k + k_tm_1 (rad/s)f\_{\text{wheel}} \approx \sqrt{\frac{k + k\_t}{m\_1}} \quad (\text{rad/s})$ → $f_wheel ≈ 12π k + k_tm_1 (Hz)f\_{\text{wheel}} \approx \frac{1}{2\pi} \sqrt{\frac{k + k\_t}{m\_1}} \quad (\text{Hz})$ → $ζ_wheel ≈ c2m_1(k + k_t)\zeta\_{\text{wheel}} \approx \frac{c}{2\sqrt{m\_1(k + k\_t)}}$
  - $f_body ≈ km_2 (rad/s)f\_{\text{body}} \approx \sqrt{\frac{k}{m\_2}} \quad (\text{rad/s})$ → $f_body ≈ 12π km_2 (Hz)f\_{\text{body}} \approx \frac{1}{2\pi} \sqrt{\frac{k}{m\_2}} \quad (\text{Hz})$ → $阻尼比ζ_body ≈ c2m_2 k阻尼比\zeta\_{\text{body}} \approx \frac{c}{2\sqrt{m\_2 k}}$
状态空间模型推导 → 为优化算法提供精确的预测模型
- 定义状态向量：
  - $[x_1 x_2 x_3 x_4]=[z_2 − z_1 z˙_2 z_1 − q z˙_1]=[悬架动行程车身速度轮胎变形量车轮速度]\boldsymbol{x} = \begin{bmatrix} x\_1 \\ x\_2 \\ x\_3 \\ x\_4 \end{bmatrix} = \begin{bmatrix} z\_2 - z\_1 \\ \dot{z}\_2 \\ z\_1 - q \\ \dot{z}\_1 \end{bmatrix} = \begin{bmatrix} 悬架动行程 \\ 车身速度 \\ 轮胎变形量 \\ 车轮速度 \end{bmatrix}$
  - 状态向量求导：
    - $x_1˙=z_2˙−z_1˙=x_2˙−x_4˙\dot{x\_{1}}=\dot{z\_{2}}-\dot{z\_{1}}=\dot{x\_{2}}-\dot{x\_{4}}$
    - $x˙_2 = z¨_2 = −km_2x_1 − cm_2(x_2 − x_4)\dot{x}\_2 = \ddot{z}\_2 = -\frac{k}{m\_2}x\_1 - \frac{c}{m\_2}(x\_2 - x\_4)$
    - $x_3˙=z_1˙−q˙=x_4−q˙\dot{x\_{3}}=\dot{z\_{1}}-\dot{q}=x\_{4}-\dot{q}$
    - $x˙_4 = z¨_1 = km_1x_1 + cm_1(x_2 − x_4) − k_tm_1x_3\dot{x}\_4 = \ddot{z}\_1 = \frac{k}{m\_1}x\_1 + \frac{c}{m\_1}(x\_2 - x\_4) - \frac{k\_t}{m\_1}x\_3$
- 矩阵形式：将四个状态方程写成矩阵形式：
  - $[x˙_1 x˙_2 x˙_3 x˙_4]=[0 1 0 −1 −km_2 −cm_2 0 cm_2 0 0 0 1 km_1 cm_1 −k_tm_1 −cm_1][x_1 x_2 x_3 x_4]+[0 0 −1 0]q˙\begin{bmatrix} \dot{x}\_1 \\ \dot{x}\_2 \\ \dot{x}\_3 \\ \dot{x}\_4 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & -1 \\ -\dfrac{k}{m\_2} & -\dfrac{c}{m\_2} & 0 & \dfrac{c}{m\_2} \\ 0 & 0 & 0 & 1 \\ \dfrac{k}{m\_1} & \dfrac{c}{m\_1} & -\dfrac{k\_t}{m\_1} & -\dfrac{c}{m\_1} \end{bmatrix} \begin{bmatrix} x\_1 \\ x\_2 \\ x\_3 \\ x\_4 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ -1 \\ 0 \end{bmatrix} \dot{q}$ → $Bq˙\dot{\bm{x}} = A\bm{x} + B\dot{q}$
    - 其中 $−km_2 −cm_2 0 cm_2 0 0 0 1 km_1 cm_1 −k_tm_1 −cm_1],B =[0 0 −1 0]A = \begin{bmatrix} 0 & 1 & 0 & -1 \\ -\dfrac{k}{m\_2} & -\dfrac{c}{m\_2} & 0 & \dfrac{c}{m\_2} \\ 0 & 0 & 0 & 1 \\ \dfrac{k}{m\_1} & \dfrac{c}{m\_1} & -\dfrac{k\_t}{m\_1} & -\dfrac{c}{m\_1} \end{bmatrix},\quad B = \begin{bmatrix} 0 \\ 0 \\ -1 \\ 0 \end{bmatrix}$
示意图：
公式推导： $m_2 z¨_2 + c(z˙_2 − z˙_1) + k(z_2 − z_1) = 0m\_2 \ddot{z}\_2 + c(\dot{z}\_2 - \dot{z}\_1) + k(z\_2 - z\_1) = 0$
- $m\_2$ 受到的弹簧力： $k(z\_2 - z\_1)$
- $m\_2$ 受到的阻尼力： $−c(z˙_2 − z˙_1)-c(\dot{z}\_2 - \dot{z}\_1)$
- $m\_2$ 的牛顿第二定律： $m_2z¨m\_{2}\ddot{z}$ = $−k(z_2 − z_1)−c(z˙_2 − z˙_1)-k(z\_2 - z\_1)-c(\dot{z}\_2 - \dot{z}\_1)$
公式推导： $m_1 z¨_1 + c(z˙_1 − z˙_2) + k(z_1 − z_2) + k_t(z_1 − q) = 0m\_1 \ddot{z}\_1 + c(\dot{z}\_1 - \dot{z}\_2) + k(z\_1 - z\_2) + k\_t(z\_1 - q) = 0$
- $m\_{1}$ 受到的弹簧力： $k(z\_2 - z\_1)$
- $m\_{1}$ 受到的弹簧力： $k(z\_1 - q)$
- $m\_{1}$ 受到的阻尼力： $c(z˙_2 − z˙_1)c(\dot{z}\_2 - \dot{z}\_1)$
  - 注释： $z˙_2 ＞ z˙_1\dot{z}\_2 ＞ \dot{z}\_1$ 时， $m\_{1}$ 相对于 $m\_{2}$ 向下运动，阻尼力向上
- $m\_1$ 的牛顿第二定律： $m_1z¨=k(z_2 − z_1)+k(z_1 − q)+c(z˙_2 − z˙_1)m\_{1}\ddot{z}=k(z\_2 - z\_1)+k(z\_1 - q)+c(\dot{z}\_2 - \dot{z}\_1)$
公式解析：
- 簧上控制簧上的加速度 $z_2¨\ddot{z\_2}$ 提高舒适性 → 半主动悬架中调节 $c$ 最小化 $z_2¨\ddot{z\_2}$
- 簧下最小化轮胎动载荷波动 → 半主动悬架中调节 $c$ 最小化 $KaTeX parse error: Undefined control sequence: \* at position 7: k\_{t}\̲*̲var(z\_1 - q)$
- 约束： $z\_2 - z\_1|≤最大行程$
  - 天棚算法：以簧上质量速度 $z_2¨\ddot{z\_2}$ 为反馈，调节 $c$ 使系统仿佛悬挂在“天空”一样，极大提升舒适性
  - 地棚算法：以簧上质量速度 $z_1¨\ddot{z\_1}$ 为反馈，优化轮胎接地性
  - 混合控制：平衡舒适与操控
  - MPC：利用该模型预测未来状态，求解最优阻尼力序列
代码举例：
- 代码流程：
  - 系统参数的定义
  - 计算系统的固有频率和阻尼比
  - 设置仿真时间、补偿与生成路面激励
  - 被动悬架计算：初始化状态→计算相对位移与相对速度 → 计算簧上簧下加速度 → 性能指标计算
  - 半主动悬架计算：初始化状态→计算相对位移与相对速度→计算期望阻尼→计算簧上簧下加速度→性能指标计算
- 指标解读
  - RMS加速度：越小越好，代表舒适性
  - 最大悬架行程：越小越好，避免机械撞击
  - 轮胎载荷变化：越小越好，代表操控稳定性
  - 阻尼系数变化：显示控制算法的决策过程
- 路面常见的激励类型
  - bump：凸块或单次冲击，模拟路面上一个孤立的、瞬态的凸起或凹陷，例如减速带、路面修补后的接缝、小坑洼等。常见形状：半正弦波、三角形、矩形凸起
  - sine：正弦波路面，模拟具有固定波长和振幅的周期性波形路面，例如老化的水泥路接缝、洗衣板路、有规律起伏的越野路面
  - random：随机路面，模拟真实世界中最常见的、不规则的路面不平度，例如普通的沥青公路、乡村土路等。其不平度统计特性符合一定的功率谱密度标准。
  - step：阶跃，模拟路面的突然高度变化，例如路缘石、深坑的边缘、铁轨等，是一种极端的bump

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

from scipy import signal

class QuarterCarModel:
    """
    1/4车辆二自由度悬架模型
    用于仿真和分析悬架系统的动态响应
    """
    
    def __init__(self, m_s=320, m_u=40, k_s=22000, k_t=200000, c_min=1000, c_max=5000):
        """
        初始化模型参数
        
        参数:
            m_s: 簧上质量 (kg) - 车身质量
            m_u: 簧下质量 (kg) - 车轮质量
            k_s: 悬架刚度 (N/m)
            k_t: 轮胎刚度 (N/m)
            c_min: 最小阻尼系数 (N·s/m)
            c_max: 最大阻尼系数 (N·s/m)
        """
        self.m_s = m_s      # 簧上质量
        self.m_u = m_u      # 簧下质量
        self.k_s = k_s      # 悬架刚度
        self.k_t = k_t      # 轮胎刚度
        self.c_min = c_min  # 最小阻尼
        self.c_max = c_max  # 最大阻尼
        
        # 计算系统的固有特性
        self.calc_natural_properties()
    
    def calc_natural_properties(self):
        """计算系统的固有频率和阻尼比"""
        # 簧上质量固有频率 (车身模态)
        self.omega_s = np.sqrt(self.k_s / self.m_s)  # rad/s
        self.f_s = self.omega_s / (2 * np.pi)        # Hz
        
        # 簧下质量固有频率 (车轮跳动模态)
        self.omega_u = np.sqrt((self.k_s + self.k_t) / self.m_u)  # rad/s
        self.f_u = self.omega_u / (2 * np.pi)                     # Hz
        
        # 阻尼比 (使用平均阻尼)
        c_avg = (self.c_min + self.c_max) / 2
        self.zeta_s = c_avg / (2 * np.sqrt(self.k_s * self.m_s))  # 车身模态阻尼比
        self.zeta_u = c_avg / (2 * np.sqrt((self.k_s + self.k_t) * self.m_u))  # 车轮模态阻尼比
        
        print(f"系统固有频率: 车身模态={self.f_s:.2f}Hz, 车轮模态={self.f_u:.2f}Hz")
        print(f"平均阻尼比: 车身模态={self.zeta_s:.3f}, 车轮模态={self.zeta_u:.3f}")
    
    def passive_suspension(self, t, road_profile, c_value):
        """
        被动悬架仿真（固定阻尼）
        
        参数:
            t: 时间向量
            road_profile: 路面输入
            c_value: 固定阻尼系数
            
        返回:
            包含各种响应的字典
        """
        dt = t[1] - t[0]  # 时间步长
        n = len(t)
        
        # 初始化状态变量
        z_s = np.zeros(n)      # 簧上质量位移
        z_u = np.zeros(n)      # 簧下质量位移
        v_s = np.zeros(n)      # 簧上质量速度
        v_u = np.zeros(n)      # 簧下质量速度
        a_s = np.zeros(n)      # 簧上质量加速度
        
        # 初始条件（静止状态）
        z_s[0] = 0
        z_u[0] = 0
        v_s[0] = 0
        v_u[0] = 0
        
        # 数值积分（前向欧拉法，简单但稳定）
        for i in range(n-1):
            # 计算相对位移和相对速度
            z_rel = z_s[i] - z_u[i]          # 悬架动行程
            v_rel = v_s[i] - v_u[i]          # 悬架相对速度
            
            # 计算加速度（牛顿第二定律）
            # 簧上质量加速度
            a_s[i] = (-self.k_s * z_rel - c_value * v_rel) / self.m_s
            
            # 簧下质量加速度
            a_u = (self.k_s * z_rel + c_value * v_rel - self.k_t * (z_u[i] - road_profile[i])) / self.m_u
            
            # 更新速度和位移
            v_s[i+1] = v_s[i] + a_s[i] * dt
            v_u[i+1] = v_u[i] + a_u * dt
            z_s[i+1] = z_s[i] + v_s[i+1] * dt
            z_u[i+1] = z_u[i] + v_u[i+1] * dt
        
        # 计算最后一个点的加速度
        z_rel_last = z_s[-1] - z_u[-1]
        v_rel_last = v_s[-1] - v_u[-1]
        a_s[-1] = (-self.k_s * z_rel_last - c_value * v_rel_last) / self.m_s
        
        # 计算性能指标
        rms_acceleration = np.sqrt(np.mean(a_s**2))  # 加速度RMS值（舒适性指标）
        max_suspension_travel = np.max(np.abs(z_s - z_u))  # 最大悬架动行程
        tire_load_variation = np.std(self.k_t * (z_u - road_profile))  # 轮胎动载荷变化（操控性指标）
        
        return {
            'time': t,
            'road': road_profile,
            'sprung_displacement': z_s,        # 簧上质量位移
            'unsprung_displacement': z_u,      # 簧下质量位移
            'sprung_acceleration': a_s,        # 簧上质量加速度
            'suspension_travel': z_s - z_u,    # 悬架动行程
            'tire_deflection': z_u - road_profile,  # 轮胎变形量
            'rms_acceleration': rms_acceleration,
            'max_suspension_travel': max_suspension_travel,
            'tire_load_variation': tire_load_variation,
            'damping_coefficient': np.ones(n) * c_value
        }
    
    def skyhook_control(self, v_s, v_rel):
        """
        天钩控制算法
        
        参数:
            v_s: 簧上质量绝对速度
            v_rel: 悬架相对速度
            
        返回:
            理想的阻尼系数
        """
        # 天钩控制增益（需要调参）
        c_sky = 3000  # 天钩阻尼系数
        
        # 理想的天钩阻尼力: F_sky = -c_sky * v_s
        # 实际的阻尼力: F_damper = -c_actual * v_rel
        # 令两者相等: c_actual = c_sky * v_s / v_rel
        
        # 避免除以零
        if abs(v_rel) < 0.001:
            return self.c_min if v_s * v_rel <= 0 else self.c_max
        
        # 计算理想阻尼系数
        c_desired = c_sky * v_s / v_rel
        
        # 确保阻尼系数非负且在规定范围内
        c_clipped = np.clip(c_desired, self.c_min, self.c_max)
        
        return c_clipped
    
    def groundhook_control(self, v_u, v_rel):
        """
        地钩控制算法
        
        参数:
            v_u: 簧下质量绝对速度
            v_rel: 悬架相对速度
            
        返回:
            理想的阻尼系数
        """
        # 地钩控制增益
        c_ground = 3000
        
        # 理想的地钩阻尼力: F_ground = -c_ground * v_u
        # 实际的阻尼力: F_damper = -c_actual * v_rel
        # 令两者相等: c_actual = c_ground * v_u / v_rel
        
        if abs(v_rel) < 0.001:
            return self.c_min if v_u * v_rel <= 0 else self.c_max
        
        c_desired = c_ground * v_u / v_rel
        c_clipped = np.clip(c_desired, self.c_min, self.c_max)
        
        return c_clipped
    
    def hybrid_control(self, v_s, v_u, v_rel, alpha=0.7):
        """
        混合控制（天钩+地钩）
        
        参数:
            v_s: 簧上质量速度
            v_u: 簧下质量速度
            v_rel: 相对速度
            alpha: 天钩权重 (0~1)，地钩权重为1-alpha
            
        返回:
            理想的阻尼系数
        """
        # 分别计算天钩和地钩的理想阻尼系数
        c_sky = self.skyhook_control(v_s, v_rel)
        c_ground = self.groundhook_control(v_u, v_rel)
        
        # 加权混合
        c_desired = alpha * c_sky + (1 - alpha) * c_ground
        
        # 确保在合理范围内
        c_clipped = np.clip(c_desired, self.c_min, self.c_max)
        
        return c_clipped
    
    def semi_active_suspension(self, t, road_profile, control_type='skyhook', control_param=None):
        """
        半主动悬架仿真
        
        参数:
            t: 时间向量
            road_profile: 路面输入
            control_type: 控制类型 ('skyhook', 'groundhook', 'hybrid')
            control_param: 控制参数（混合控制的alpha值）
            
        返回:
            包含各种响应的字典
        """
        dt = t[1] - t[0]
        n = len(t)
        
        # 初始化状态变量
        z_s = np.zeros(n)      # 簧上质量位移
        z_u = np.zeros(n)      # 簧下质量位移
        v_s = np.zeros(n)      # 簧上质量速度
        v_u = np.zeros(n)      # 簧下质量速度
        a_s = np.zeros(n)      # 簧上质量加速度
        c_array = np.zeros(n)  # 阻尼系数变化
        
        # 初始条件
        z_s[0] = 0
        z_u[0] = 0
        v_s[0] = 0
        v_u[0] = 0
        c_array[0] = self.c_min
        
        # 混合控制参数
        alpha = control_param if control_param is not None else 0.7
        
        # 数值积分
        for i in range(n-1):
            # 计算相对位移和相对速度
            z_rel = z_s[i] - z_u[i]
            v_rel = v_s[i] - v_u[i]
            
            # 根据控制策略计算阻尼系数
            if control_type == 'skyhook':
                c_array[i] = self.skyhook_control(v_s[i], v_rel)
            elif control_type == 'groundhook':
                c_array[i] = self.groundhook_control(v_u[i], v_rel)
            elif control_type == 'hybrid':
                c_array[i] = self.hybrid_control(v_s[i], v_u[i], v_rel, alpha)
            else:
                raise ValueError(f"未知的控制类型: {control_type}")
            
            # 计算加速度
            a_s[i] = (-self.k_s * z_rel - c_array[i] * v_rel) / self.m_s
            a_u = (self.k_s * z_rel + c_array[i] * v_rel - self.k_t * (z_u[i] - road_profile[i])) / self.m_u
            
            # 更新状态
            v_s[i+1] = v_s[i] + a_s[i] * dt
            v_u[i+1] = v_u[i] + a_u * dt
            z_s[i+1] = z_s[i] + v_s[i+1] * dt
            z_u[i+1] = z_u[i] + v_u[i+1] * dt
        
        # 计算最后一个点
        z_rel_last = z_s[-1] - z_u[-1]
        v_rel_last = v_s[-1] - v_u[-1]
        
        # 最后一点的阻尼系数
        if control_type == 'skyhook':
            c_array[-1] = self.skyhook_control(v_s[-1], v_rel_last)
        elif control_type == 'groundhook':
            c_array[-1] = self.groundhook_control(v_u[-1], v_rel_last)
        elif control_type == 'hybrid':
            c_array[-1] = self.hybrid_control(v_s[-1], v_u[-1], v_rel_last, alpha)
        
        a_s[-1] = (-self.k_s * z_rel_last - c_array[-1] * v_rel_last) / self.m_s
        
        # 计算性能指标
        rms_acceleration = np.sqrt(np.mean(a_s**2))
        max_suspension_travel = np.max(np.abs(z_s - z_u))
        tire_load_variation = np.std(self.k_t * (z_u - road_profile))
        
        return {
            'time': t,
            'road': road_profile,
            'sprung_displacement': z_s,
            'unsprung_displacement': z_u,
            'sprung_acceleration': a_s,
            'suspension_travel': z_s - z_u,
            'tire_deflection': z_u - road_profile,
            'rms_acceleration': rms_acceleration,
            'max_suspension_travel': max_suspension_travel,
            'tire_load_variation': tire_load_variation,
            'damping_coefficient': c_array,
            'control_type': control_type
        }
    
    def generate_road_profile(self, t, profile_type='bump', amplitude=0.05, frequency=1.0):
        """
        生成路面激励
        
        参数:
            t: 时间向量
            profile_type: 路面类型 ('bump', 'sine', 'random', 'step')
            amplitude: 激励幅值 (m)
            frequency: 激励频率 (Hz，仅对正弦波有效)
            
        返回:
            路面位移向量
        """
        if profile_type == 'bump':
            # 单凸起路面（常用测试工况）
            road = np.zeros_like(t)
            bump_time = 1.0  # 凸起发生的时间
            bump_duration = 0.2  # 凸起持续时间
            
            # 创建半正弦凸起
            mask = (t >= bump_time) & (t <= bump_time + bump_duration)
            road[mask] = amplitude * np.sin(np.pi * (t[mask] - bump_time) / bump_duration)
            
        elif profile_type == 'sine':
            # 正弦波路面
            road = amplitude * np.sin(2 * np.pi * frequency * t)
            
        elif profile_type == 'step':
            # 阶跃输入（模拟过台阶）
            road = np.zeros_like(t)
            step_time = 1.0
            road[t >= step_time] = amplitude
            
        elif profile_type == 'random':
            # 随机路面（更真实的工况）
            # 使用低通滤波器生成有色噪声
            np.random.seed(42)  # 固定随机种子以便重复实验
            white_noise = np.random.randn(len(t))
            b, a = signal.butter(2, 0.1)  # 低通滤波器
            road = signal.filtfilt(b, a, white_noise) * amplitude
            
        else:
            raise ValueError(f"未知的路面类型: {profile_type}")
        
        return road

def plot_comparison(results_passive, results_semi, title_suffix=""):
    """
    绘制被动悬架和半主动悬架的对比图
    """
    fig = plt.figure(figsize=(16, 12))
    
    # 1. 路面输入
    ax1 = plt.subplot(4, 2, 1)
    ax1.plot(results_passive['time'], results_passive['road'], 'k-', linewidth=2, label='路面输入')
    ax1.set_ylabel('位移 (m)')
    ax1.set_title(f'路面激励 {title_suffix}')
    ax1.grid(True, alpha=0.3)
    ax1.legend()
    
    # 2. 车身加速度对比
    ax2 = plt.subplot(4, 2, 2)
    ax2.plot(results_passive['time'], results_passive['sprung_acceleration'], 'b-', 
             label=f"被动 (RMS={results_passive['rms_acceleration']:.3f}m/s²)")
    ax2.plot(results_semi['time'], results_semi['sprung_acceleration'], 'r-', 
             label=f"半主动 (RMS={results_semi['rms_acceleration']:.3f}m/s²)")
    ax2.set_ylabel('加速度 (m/s²)')
    ax2.set_title('车身加速度对比 (舒适性指标)')
    ax2.grid(True, alpha=0.3)
    ax2.legend()
    
    # 3. 悬架动行程对比
    ax3 = plt.subplot(4, 2, 3)
    ax3.plot(results_passive['time'], results_passive['suspension_travel'], 'b-', 
             label=f"被动 (最大={results_passive['max_suspension_travel']*100:.1f}cm)")
    ax3.plot(results_semi['time'], results_semi['suspension_travel'], 'r-', 
             label=f"半主动 (最大={results_semi['max_suspension_travel']*100:.1f}cm)")
    ax3.set_ylabel('位移 (m)')
    ax3.set_title('悬架动行程对比 (机械约束)')
    ax3.grid(True, alpha=0.3)
    ax3.legend()
    
    # 4. 轮胎变形量对比
    ax4 = plt.subplot(4, 2, 4)
    ax4.plot(results_passive['time'], results_passive['tire_deflection'], 'b-', 
             label=f"被动 (标准差={results_passive['tire_load_variation']/1000:.2f}kN)")
    ax4.plot(results_semi['time'], results_semi['tire_deflection'], 'r-', 
             label=f"半主动 (标准差={results_semi['tire_load_variation']/1000:.2f}kN)")
    ax4.set_ylabel('位移 (m)')
    ax4.set_title('轮胎变形量对比 (操控性指标)')
    ax4.grid(True, alpha=0.3)
    ax4.legend()
    
    # 5. 车身位移对比
    ax5 = plt.subplot(4, 2, 5)
    ax5.plot(results_passive['time'], results_passive['sprung_displacement'], 'b-', label='被动')
    ax5.plot(results_semi['time'], results_semi['sprung_displacement'], 'r-', label='半主动')
    ax5.set_xlabel('时间 (s)')
    ax5.set_ylabel('位移 (m)')
    ax5.set_title('车身位移对比')
    ax5.grid(True, alpha=0.3)
    ax5.legend()
    
    # 6. 车轮位移对比
    ax6 = plt.subplot(4, 2, 6)
    ax6.plot(results_passive['time'], results_passive['unsprung_displacement'], 'b-', label='被动')
    ax6.plot(results_semi['time'], results_semi['unsprung_displacement'], 'r-', label='半主动')
    ax6.set_xlabel('时间 (s)')
    ax6.set_ylabel('位移 (m)')
    ax6.set_title('车轮位移对比')
    ax6.grid(True, alpha=0.3)
    ax6.legend()
    
    # 7. 阻尼系数变化
    ax7 = plt.subplot(4, 2, 7)
    ax7.plot(results_passive['time'], results_passive['damping_coefficient'], 'b-', 
             label=f"被动 (固定={results_passive['damping_coefficient'][0]:.0f}N·s/m)")
    ax7.plot(results_semi['time'], results_semi['damping_coefficient'], 'r-', 
             label=f"半主动 ({results_semi.get('control_type', '自适应')})")
    ax7.set_xlabel('时间 (s)')
    ax7.set_ylabel('阻尼系数 (N·s/m)')
    ax7.set_title('阻尼系数变化')
    ax7.grid(True, alpha=0.3)
    ax7.legend()
    
    # 8. 性能指标总结
    ax8 = plt.subplot(4, 2, 8)
    metrics = ['舒适性\n(RMS加速度)', '悬架行程\n(最大值)', '轮胎载荷\n(标准差)']
    passive_vals = [
        results_passive['rms_acceleration'],
        results_passive['max_suspension_travel'],
        results_passive['tire_load_variation']/1000
    ]
    semi_vals = [
        results_semi['rms_acceleration'],
        results_semi['max_suspension_travel'],
        results_semi['tire_load_variation']/1000
    ]
    
    x = np.arange(len(metrics))
    width = 0.35
    ax8.bar(x - width/2, passive_vals, width, label='被动悬架', color='blue', alpha=0.7)
    ax8.bar(x + width/2, semi_vals, width, label='半主动悬架', color='red', alpha=0.7)
    
    ax8.set_xlabel('性能指标')
    ax8.set_ylabel('数值')
    ax8.set_title('性能指标对比')
    ax8.set_xticks(x)
    ax8.set_xticklabels(metrics)
    ax8.grid(True, alpha=0.3, axis='y')
    ax8.legend()
    
    plt.suptitle(f'1/4车辆悬架模型仿真 - {title_suffix}', fontsize=16, y=1.02)
    plt.tight_layout()
    plt.show()

def main():
    """
    主函数：运行悬架模型仿真和对比
    """
    # 1. 创建悬架模型实例
    print("=" * 60)
    print("1/4车辆二自由度悬架模型仿真")
    print("=" * 60)
    
    # 使用电动车典型参数
    model = QuarterCarModel(
        m_s=400,     # 电动车簧上质量更大（电池重）
        m_u=45,      # 簧下质量
        k_s=25000,   # 悬架刚度
        k_t=220000,  # 轮胎刚度
        c_min=800,   # 最小阻尼
        c_max=6000   # 最大阻尼
    )
    
    # 2. 设置仿真时间
    dt = 0.001      # 时间步长 (1ms)
    t_max = 5.0     # 总仿真时间
    t = np.arange(0, t_max, dt)
    
    # 3. 生成路面激励
    road_profile = model.generate_road_profile(
        t, 
        profile_type='step',  # 尝试 'bump', 'sine', 'random', 'step'
        amplitude=0.05,       # 5cm凸起
        frequency=1.0
    )
    
    # 4. 仿真被动悬架（固定阻尼）
    print("\n仿真被动悬架...")
    c_passive = 2000  # 固定阻尼系数
    results_passive = model.passive_suspension(t, road_profile, c_passive)
    
    # 5. 仿真半主动悬架（天钩控制）
    print("仿真半主动悬架（天钩控制）...")
    results_semi = model.semi_active_suspension(
        t, road_profile, 
        control_type='hybrid'  # 尝试 'skyhook', 'groundhook', 'hybrid'
    )
    
    # 6. 打印性能对比
    print("\n" + "=" * 60)
    print("性能对比结果:")
    print("=" * 60)
    print(f"{'指标':<20} {'被动悬架':<15} {'半主动悬架':<15} {'改善率':<10}")
    print("-" * 60)
    
    # 计算各项指标的改善率
    acc_improvement = (results_passive['rms_acceleration'] - results_semi['rms_acceleration']) / results_passive['rms_acceleration'] * 100
    travel_improvement = (results_passive['max_suspension_travel'] - results_semi['max_suspension_travel']) / results_passive['max_suspension_travel'] * 100
    tire_improvement = (results_passive['tire_load_variation'] - results_semi['tire_load_variation']) / results_passive['tire_load_variation'] * 100
    
    print(f"{'RMS加速度(m/s²)':<20} {results_passive['rms_acceleration']:<15.3f} {results_semi['rms_acceleration']:<15.3f} {acc_improvement:>8.1f}%")
    print(f"{'最大悬架行程(cm)':<20} {results_passive['max_suspension_travel']*100:<15.1f} {results_semi['max_suspension_travel']*100:<15.1f} {travel_improvement:>8.1f}%")
    print(f"{'轮胎载荷标准差(kN)':<20} {results_passive['tire_load_variation']/1000:<15.2f} {results_semi['tire_load_variation']/1000:<15.2f} {tire_improvement:>8.1f}%")
    
    # 7. 绘制对比图
    plot_comparison(results_passive, results_semi, title_suffix="凸起路面 - 天钩控制")
    
    # 8. 额外分析：不同控制策略对比
    print("\n" + "=" * 60)
    print("不同控制策略对比:")
    print("=" * 60)
    
    control_strategies = ['skyhook', 'groundhook', 'hybrid']
    results_all = {}
    
    for strategy in control_strategies:
        if strategy == 'hybrid':
            results = model.semi_active_suspension(t, road_profile, control_type=strategy, control_param=0.7)
        else:
            results = model.semi_active_suspension(t, road_profile, control_type=strategy)
        
        results_all[strategy] = results
        print(f"{strategy:>10}: RMS加速度={results['rms_acceleration']:.3f}m/s², "
              f"最大行程={results['max_suspension_travel']*100:.1f}cm, "
              f"轮胎载荷标准差={results['tire_load_variation']/1000:.2f}kN")
    
    # 9. 绘制不同控制策略的阻尼系数变化
    plt.figure(figsize=(12, 4))
    for i, strategy in enumerate(control_strategies):
        plt.subplot(1, 3, i+1)
        plt.plot(t, results_all[strategy]['damping_coefficient'], 'r-')
        plt.fill_between(t, model.c_min, model.c_max, alpha=0.1, color='gray')
        plt.xlabel('时间 (s)')
        plt.ylabel('阻尼系数 (N·s/m)')
        plt.title(f'{strategy}控制策略')
        plt.grid(True, alpha=0.3)
        plt.ylim([model.c_min-500, model.c_max+500])
    
    plt.suptitle('不同控制策略的阻尼系数变化', fontsize=14, y=1.05)
    plt.tight_layout()
    plt.show()
    
    return model, results_passive, results_semi, results_all

if __name__ == "__main__":
    # 运行主程序
    model, results_passive, results_semi, results_all = main()
    
    print("\n" + "=" * 60)
    print("仿真完成！")
    print("=" * 60)

天棚算法Skyhook

算法简介：用于汽车半主动悬挂系统的控制算法，旨在减轻路面颠簸对车身的影响。其核心思想是通过调节减振器的阻尼力，使车身保持相对稳定，从而提高乘坐舒适性和车辆操控性。
核心思想：想象在车身与固定不动的天空之间连接一个阻尼器，这个"天棚阻尼器"只对车身的绝对运动产生阻尼力，而不受车轮运动的影响。（理想天棚系统中，阻尼器连接车身和固定的天空，这意味着阻尼力只与车身的绝对速度有关，可以最有效地抑制车身的振动，而不受车轮运动的影响）
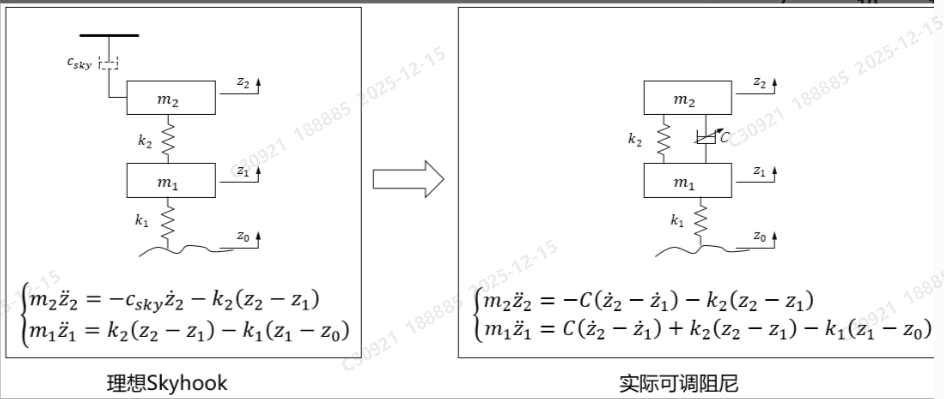
公式：
- 让实际系统的车身动力学与理想系统一致，即让两个系统的车身方程等价：
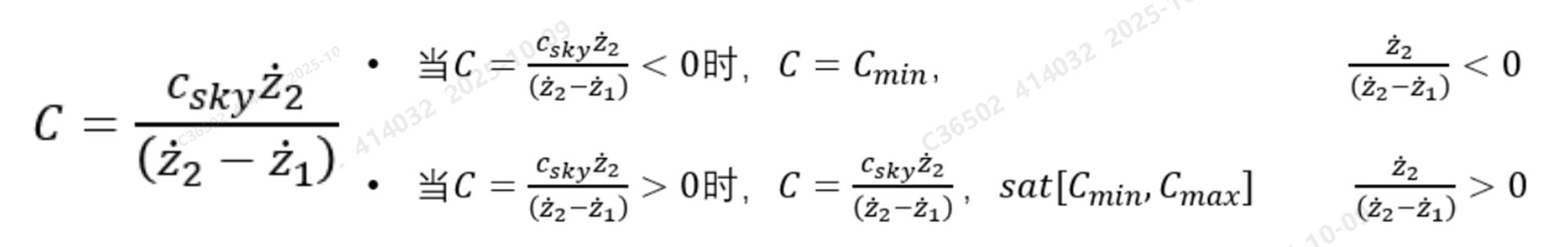
- - 注释：减振器做不到负的阻尼系数，那只能提供最小阻尼了。如果能达到0，当然最好了，但任何一种液压阻尼可调减振器，阻尼系数都不可能做到0，是有下边界。
  - 当算法请求阻尼系数为正的时候，需要限制在最小最大边界
- $C\_{sky}$ 的值怎么确定呢？目前是依据经验值
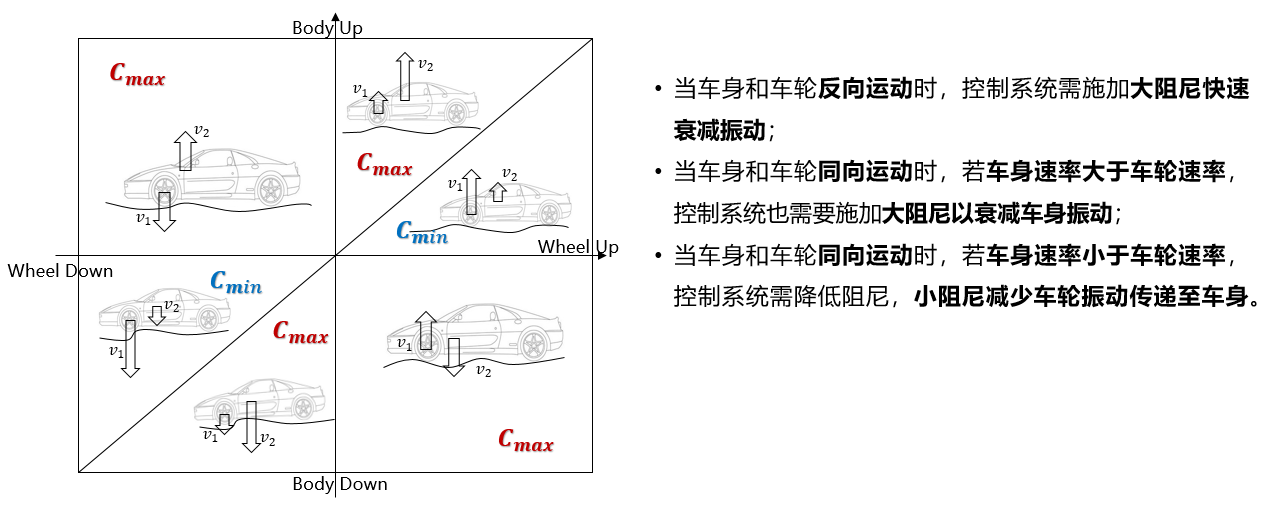
图解：
- 当车身和车轮反向运动时，控制系统需施加大阻尼快速衰减振动
  - 注释：车轮已经过了减速带最高点，开始向下运动 (v₁ < 0)，但车身由于惯性还在向上运动 (v₂ > 0)，此时悬架被拉伸，需要大阻尼抑制反弹
- 当车身和车轮同向运动时，若车身速率大于车轮速率，控制系统需要施加大阻尼衰减车身振动
  - 注释：提升舒适性：直接针对车身加速度（舒适性指标）进行控制
- 当车身和车轮同向运动时，若车身速率小于车轮速率，控制系统需降低阻尼，小阻尼减少车轮振动传递至车身
  - 例如，v1>V2且方向向上，此时m2的阻尼力方向为正向，大小为 $−c(z˙_2 − z˙_1)-c(\dot{z}\_2 - \dot{z}\_1)$ ，这个力通过悬架推着车身向上加速，我们减小阻尼可以减小这个里的大小

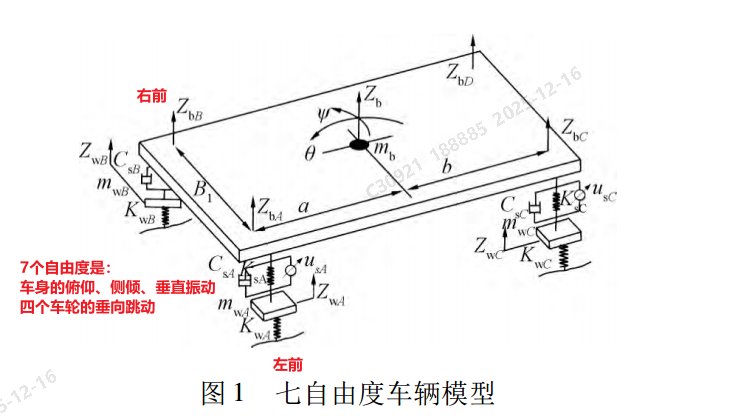
悬架七自由度方程

整车的七自由度方程
- 公式：
  - ① 四个车轮的垂直位移：
    - 一般形式
      - $z_bA = z_b + aθ_b + B_f2ϕ z_bB = z_b + aθ_b − B_f2ϕ z_bC = z_b − bθ_b + B_r2ϕ z_bD = z_b − bθ_b − B_r2ϕ\begin{aligned} z\_{bA} &= z\_b + a\theta\_b + \frac{B\_f}{2}\phi \\ z\_{bB} &= z\_b + a\theta\_b - \frac{B\_f}{2}\phi \\ z\_{bC} &= z\_b - b\theta\_b + \frac{B\_r}{2}\phi \\ z\_{bD} &= z\_b - b\theta\_b - \frac{B\_r}{2}\phi \end{aligned}$
    - 矩阵形式：
      - $KaTeX parse error: Undefined control sequence: \* at position 229: …2 \end{bmatrix}\̲*̲\begin{bmatrix}…$
  - ② 车身质心处垂向运动方程为:
    - $KaTeX parse error: {split} can be used only in display mode.$
  - ③ 车身侧倾运动方程为：
    - $KaTeX parse error: {split} can be used only in display mode.$
  - ④ 车身俯仰运动方程为：
    - $KaTeX parse error: {split} can be used only in display mode.$
  - ⑤ 四个非簧载质量(簧下质量)运动方程：
    - $m_wA z¨_wA = k_tA(z_gA − z_wA) + k_sA(z_bA − z_wA) + C_sA(z˙_bA − z˙_wA) m_wB z¨_wB = k_tB(z_gB − z_wB) + k_sB(z_bB − z_wB) + C_sB(z˙_bB − z˙_wB) m_wC z¨_wC = k_tC(z_gC − z_wC) + k_sC(z_bC − z_wC) + C_sC(z˙_bC − z˙_wC) m_wD z¨_wD = k_tD(z_gD − z_wD) + k_sD(z_bD − z_wD) + C_sD(z˙_bD − z˙_wD)\begin{aligned} m\_{wA} \ddot{z}\_{wA} &= k\_{tA}(z\_{gA} - z\_{wA}) + k\_{sA}(z\_{bA} - z\_{wA}) + C\_{sA}(\dot{z}\_{bA} - \dot{z}\_{wA}) \\ m\_{wB} \ddot{z}\_{wB} &= k\_{tB}(z\_{gB} - z\_{wB}) + k\_{sB}(z\_{bB} - z\_{wB}) + C\_{sB}(\dot{z}\_{bB} - \dot{z}\_{wB}) \\ m\_{wC} \ddot{z}\_{wC} &= k\_{tC}(z\_{gC} - z\_{wC}) + k\_{sC}(z\_{bC} - z\_{wC}) + C\_{sC}(\dot{z}\_{bC} - \dot{z}\_{wC}) \\ m\_{wD} \ddot{z}\_{wD} &= k\_{tD}(z\_{gD} - z\_{wD}) + k\_{sD}(z\_{bD} - z\_{wD}) + C\_{sD}(\dot{z}\_{bD} - \dot{z}\_{wD}) \end{aligned}$
- 字母释义：
  - $z\_{b}$ ：车身质心处的垂直位移
  - $z\_{gA}$ $z\_{gB}$ $z\_{gC}$ $z\_{gD}$ ：每个轮的路面激励，表示路面垂直位移
  - ${z}\_{bA}$ ${z}\_{bB }$ ${z}\_{bC}$ ${z}\_{bD}$ ：左前、右前、左后、右后车身四个角落簧上位移（向上为正）
  - ${z}\_{wA}$ ${z}\_{wB }$ ${z}\_{wC}$ ${z}\_{wD}$ ：左前、右前、左后、右后四个车轮的垂直位移（向上为正）
  - $a$ $b$ ：前轴/后轴到车身质心的水平距离
  - $θ_b\theta\_b$ ：俯仰角（绕车身横轴，前俯为正）
  - $ϕ\phi$ ：侧倾角（绕车身纵轴，左倾为正）
  - $B\_{f}$ $B\_{r}$ ：前轮和后轮的轮距
  - $k\_{sA}$ $k\_{sB}$ $k\_{sC}$ $k\_{sD}$ ：左前、右前、左后、右后四个悬架的弹簧刚度
  - $C\_{sA}$ $C\_{sB}$ $C\_{sC}$ $C\_{sD}$ ：左前、右前、左后、右后四个悬架的阻尼系数
  - $m\_{wA}$ $m\_{wB}$ $m\_{wC}$ $m\_{wD}$ ：每个轮的非簧载质量，包括车轮、制动器、轮毂等
  - $I\_p$ ：车身绕y轴的转动惯量
  - $θ¨_b\ddot\theta\_{b}$ ：俯仰角加速度
车身四个角落簧上位移：
- $z_bA = z_b + aθ_b + B_f2ϕ z_bB = z_b + aθ_b − B_f2ϕ z_bC = z_b − bθ_b + B_r2ϕ z_bD = z_b − bθ_b − B_r2ϕ\begin{aligned} z\_{bA} &= z\_b + a\theta\_b + \frac{B\_f}{2}\phi \\ z\_{bB} &= z\_b + a\theta\_b - \frac{B\_f}{2}\phi \\ z\_{bC} &= z\_b - b\theta\_b + \frac{B\_r}{2}\phi \\ z\_{bD} &= z\_b - b\theta\_b - \frac{B\_r}{2}\phi \end{aligned}$
  - $z\_{b}$ ：车身质心处的垂直位移
  - $z\_{bA}$ $z\_{bB}$ $z\_{bC}$ $z\_{bD}$ ：左前、右前、左后、右后四个角落车身的垂直位移
  - $a$ $b$ ：前轴/后轴到车身质心的水平距离
  - $θ_b\theta\_b$ ：俯仰角（绕车身横轴，前俯为正）
  - $ϕ\phi$ ：侧倾角（绕车身纵轴，左倾为正）
  - $B\_{f}$ $B\_{r}$ ：前轮和后轮的轮距
- 公式推导：
  - 坐标系建立：原点是车身的质心，x 轴：指向车辆前进方向（向前为正），y 轴：指向车辆右侧（向右为正），z 轴：垂直向上（向上为正）。
  - 基于坐标系得到车身四个角落的坐标：
    - 前左（A点）： $a, -B\_f/2)$
    - 前右（B点）： $a, B\_f/2)$
    - 后左（C点）： $b, -B\_r/2)$
    - 后右（D点）： $b, B\_r/2)$
  - 当俯仰角和侧倾角都比较小的时候，用线性近似。对于车身上任意一点 $(x, y)$ 其垂直位移 $z$ 由三部分叠加：
    - 质心平移 $z\_{b}$
    - 俯仰运动引起的垂直位移：绕x轴旋转该点的垂直位移变化约为 $xθ_b- x\theta\_b$
    - 侧倾引起的垂直位移：绕y轴旋转该点的垂直位移变化约为 $B_f2ϕ\frac{B\_f}{2}\phi$
    - 带入上述得到车身四个点的垂直坐标
车身质心处垂向运动方程为
- $KaTeX parse error: {split} can be used only in display mode.$
  - ${z}\_{bA}$ ${z}\_{bB }$ ${z}\_{bC}$ ${z}\_{bD}$ ：左前、右前、左后、右后车身四个角落簧上位移（向上为正）
  - ${z}\_{wA}$ ${z}\_{wB }$ ${z}\_{wC}$ ${z}\_{wD}$ ：左前、右前、左后、右后四个车轮的垂直位移（向上为正）
  - $k\_{sA}$ $k\_{sB}$ $k\_{sC}$ $k\_{sD}$ ：左前、右前、左后、右后四个悬架的弹簧刚度
  - $C\_{sA}$ $C\_{sB}$ $C\_{sC}$ $C\_{sD}$ ：左前、右前、左后、右后四个悬架的阻尼系数
- 公式推导：对于每个悬架点（车身角落），悬架作用于车身的力（向上为正）包括弹簧力和阻尼力，牛二律为：
  - $m_iz_i¨ = k_si(z_bi − z_wi) + c_si(z˙_bi − z˙_wi), i = A, B, C, Dm\_{i}\ddot{z\_{i}} = k\_{si}(z\_{bi} - z\_{wi}) + c\_{si}(\dot{z}\_{bi} - \dot{z}\_{wi}), \quad i = A, B, C, D$
  - 车身质心垂直方向的合力等于质量乘以加速度，于是得到车身垂直运动方程
- 方程第二部意义：车身质心垂直加速度与四个悬架点相对位移和相对速度的关系。通过控制悬架阻尼系数 Csi（如在CDC控制中），可以调节车身垂直振动响应，优化舒适性和操控性。
车身俯仰运动方程为
- $KaTeX parse error: {split} can be used only in display mode.$
- 公式推导：
  - 俯仰方向力矩平衡：车身绕y轴的转动惯量为 $I\_p$ ，俯仰角加速度为 $θ¨_b\ddot\theta\_{b}$ ，根据刚体的转动定律有： $I_y θ¨_b = ∑ M_yI\_y \ddot{\theta}\_b = \sum M\_y$ ，其中 $M\_y$ 为所有外力对y轴的力矩之和，其中每个悬架力 $F\_{si}$ 对y轴的力矩计算如下（基于位置矢量与力的叉乘）：
    - 前左（A点） $a, -B\_f/2)$ 力矩y分量 $a F\_{sA}$
    - 前右（B点） $a, B\_f/2)$ 力矩y分量 $a F\_{sB}$
    - 后左（C点） $b, -B\_f/2)$ 力矩y分量 $b F\_{sC}$
    - 后右（D点） $b, -B\_f/2)$ 力矩y分量 $b F\_{sD}$
    - 总的俯仰力矩为： $M_y = −a(F_sA + F_sB) + b(F_sC + F_sD)\sum M\_y = -a(F\_{sA} + F\_{sB}) + b(F\_{sC} + F\_{sD})$
    - 每个 $F\_{si}$ 的表达式为： $F_si=k_si(z_bi − z_wi) + c_si(z˙_bi − z˙_wi), i = A, B, C, DF\_{si}=k\_{si}(z\_{bi} - z\_{wi}) + c\_{si}(\dot{z}\_{bi} - \dot{z}\_{wi}), \quad i = A, B, C, D$
  - 对于每个悬架点（车身角落），悬架作用于车身的力（向上为正）包括弹簧力和阻尼力，牛二律为：
车身侧倾运动方程：
- $KaTeX parse error: Undefined control sequence: \[ at position 25: …t{\phi} = \left\̲[̲ -C\_{sA}(\dot{…$
- 公式推导和上面差不多
四个非簧载质量(簧下质量)运动方程：
- $m_wA z¨_wA = k_tA(z_gA − z_wA) + k_sA(z_bA − z_wA) + C_sA(z˙_bA − z˙_wA) m_wB z¨_wB = k_tB(z_gB − z_wB) + k_sB(z_bB − z_wB) + C_sB(z˙_bB − z˙_wB) m_wC z¨_wC = k_tC(z_gC − z_wC) + k_sC(z_bC − z_wC) + C_sC(z˙_bC − z˙_wC) m_wD z¨_wD = k_tD(z_gD − z_wD) + k_sD(z_bD − z_wD) + C_sD(z˙_bD − z˙_wD)\begin{aligned} m\_{wA} \ddot{z}\_{wA} &= k\_{tA}(z\_{gA} - z\_{wA}) + k\_{sA}(z\_{bA} - z\_{wA}) + C\_{sA}(\dot{z}\_{bA} - \dot{z}\_{wA}) \\ m\_{wB} \ddot{z}\_{wB} &= k\_{tB}(z\_{gB} - z\_{wB}) + k\_{sB}(z\_{bB} - z\_{wB}) + C\_{sB}(\dot{z}\_{bB} - \dot{z}\_{wB}) \\ m\_{wC} \ddot{z}\_{wC} &= k\_{tC}(z\_{gC} - z\_{wC}) + k\_{sC}(z\_{bC} - z\_{wC}) + C\_{sC}(\dot{z}\_{bC} - \dot{z}\_{wC}) \\ m\_{wD} \ddot{z}\_{wD} &= k\_{tD}(z\_{gD} - z\_{wD}) + k\_{sD}(z\_{bD} - z\_{wD}) + C\_{sD}(\dot{z}\_{bD} - \dot{z}\_{wD}) \end{aligned}$
  - $z\_{gA}$ $z\_{gB}$ $z\_{gC}$ $z\_{gD}$ ：每个轮的路面激励，表示路面垂直位移
  - $m\_{wA}$ $m\_{wB}$ $m\_{wC}$ $m\_{wD}$ ：每个轮的非簧载质量，包括车轮、制动器、轮毂等
- 公式推导：参考双质量系统震动方程
矩阵化表示：
- 四个车身的垂直状态： $KaTeX parse error: Undefined control sequence: \* at position 229: …2 \end{bmatrix}\̲*̲\begin{bmatrix}…$
- 四个车身悬架力： $Z_w − L X_body\mathbf{D} = \mathbf{Z}\_w - \mathbf{L} \mathbf{X}\_{\text{body}}$ $F_susp =C_s D˙ + K_s D\mathbf{F}\_{\text{susp}} =\mathbf{C}\_s \dot{\mathbf{D}} + \mathbf{K}\_s \mathbf{D}$
  - 定义：悬架相对位移 $d_A d_B d_C d_D ]= [ z_wA − z_bA z_wB − z_bB z_wC − z_bC z_wD − z_bD ]=Z_w − Z_b = Z_w − L X_body\mathbf{D} = \begin{bmatrix} d\_A \\ d\_B \\ d\_C \\ d\_D \end{bmatrix}= \begin{bmatrix} z\_{wA} - z\_{bA} \\ z\_{wB} - z\_{bB} \\ z\_{wC} - z\_{bC} \\ z\_{wD} - z\_{bD} \end{bmatrix}=\mathbf{Z}\_w - \mathbf{Z}\_b = \mathbf{Z}\_w - \mathbf{L} \mathbf{X}\_{\text{body}}$
  - 定义：悬架相对速度 $d˙_A d˙_B d˙_C d˙_D ]=[ z_wA˙ − z_bA˙ z_wB˙ − z_bB˙ z_wC˙ − z_bC˙ z_wD˙ − z_bD˙ ]\dot{\mathbf{D}} = \begin{bmatrix} \dot{d}\_A \\ \dot{d}\_B \\ \dot{d}\_C \\ \dot{d}\_D \end{bmatrix}=\begin{bmatrix} \dot{z\_{wA}} - \dot{z\_{bA}} \\ \dot{z\_{wB}} - \dot{z\_{bB}} \\ \dot{z\_{wC}} - \dot{z\_{bC}} \\ \dot{z\_{wD}} - \dot{z\_{bD}} \end{bmatrix}$
  - 定义：每个悬架的力(阻尼力+弹簧力) $F_susp = [ f_A f_B f_C f_D ]= [ C_sA d˙_A + k_sA d_A C_sB d˙_B + k_sB d_iB C_sC d˙_C + k_sC d_C C_sD d˙_D + k_sD d_D ]=C_s D˙ + K_s D\mathbf{F}\_{\text{susp}} = \begin{bmatrix} f\_A \\ f\_B \\ f\_C \\ f\_D \end{bmatrix}= \begin{bmatrix} C\_{sA} \dot{d}\_A + k\_{sA} d\_A \\ C\_{sB} \dot{d}\_B + k\_{sB} d\_iB\\ C\_{sC} \dot{d}\_C + k\_{sC} d\_C \\ C\_{sD} \dot{d}\_D + k\_{sD} d\_D \end{bmatrix}=\mathbf{C}\_s \dot{\mathbf{D}} + \mathbf{K}\_s \mathbf{D}$
  - 定义阻尼对角矩阵： $C_s = diag(C_sA, C_sB, C_sC, C_sD)\mathbf{C}\_s = \mathrm{diag}(C\_{sA}, C\_{sB}, C\_{sC}, C\_{sD})$
  - 定义悬架刚度对角矩阵： $K_s = diag(k_sA, k_sB, k_sC, k_sD)\mathbf{K}\_s = \mathrm{diag}(k\_{sA}, k\_{sB}, k\_{sC}, k\_{sD})$
- 车身垂直运动方程： $m_b z¨_b = f_A + f_B + f_C + f_D = 1T F_suspm\_b \ddot{z}\_b = f\_A + f\_B + f\_C + f\_D = \mathbf{1}^T \mathbf{F}\_{\text{susp}}$
  - 定义： $KaTeX parse error: Undefined control sequence: \[ at position 16: \mathbf{1}^T = \̲[̲1, 1, 1, 1\]$
- 车身俯仰运动方程： $I_p θ¨_b = b(f_C + f_D) − a(f_A + f_B) = r_pT F_suspI\_p \ddot{\theta}\_b = b(f\_C + f\_D) - a(f\_A + f\_B) = \mathbf{r}\_p^T \mathbf{F}\_{\text{susp}}$
  - 定义： $KaTeX parse error: Undefined control sequence: \[ at position 19: …thbf{r}\_p^T = \̲[̲-a, -a, b, b\]$
- 车身侧倾运动方程： $I_r ϕ¨ = (−f_A + f_B)B_f2 + (−f_C + f_D)B_r2 = r_rT F_suspI\_r \ddot{\phi} = (-f\_A + f\_B)\frac{B\_f}{2} + (-f\_C + f\_D)\frac{B\_r}{2} = \mathbf{r}\_r^T \mathbf{F}\_{\text{susp}}$
  - 定义： $KaTeX parse error: Undefined control sequence: \[ at position 24: …r}\_r^T = \left\̲[̲ -\frac{B\_f}{2…$
- 化简： $\ddot{X} + C \dot{X} + K X = K'\_t Z\_g$
  - 质量矩阵： $diag(m_b, I_p, I_r, m_wA, m_wB, m_wC, m_wD)M = \text{diag}(m\_b, I\_p, I\_r, m\_{wA}, m\_{wB}, m\_{wC}, m\_{wD})$
  - 阻尼矩阵： $C_s H C_s H]C = \begin{bmatrix} -A C\_s H \\ C\_s H \end{bmatrix}$
  - 刚度矩阵： $K_s H K_s H + K_t E]K = \begin{bmatrix} -A K\_s H \\ K\_s H + K\_t E \end{bmatrix}$
  - 路面激励系数矩阵： $K′_t = [0_3 × 4 K_t]K'\_t = \begin{bmatrix} 0\_{3 \times 4} \\ K\_t \end{bmatrix}$
  - 几何关系矩阵： $B_f2 1 a −B_f2 1 −b B_r2 1 −b −B_r2]H = \begin{bmatrix} 1 & a & \frac{B\_f}{2} \\ 1 & a & -\frac{B\_f}{2} \\ 1 & -b & \frac{B\_r}{2} \\ 1 & -b & -\frac{B\_r}{2} \end{bmatrix}$
- 不加主动控制力的化简详细形式： $[M_b 0 0 M_w][X¨_body Z¨_w]+[−A C_s H C_s H]X˙+[−A K_s H K_s H + K_t E]X =[0 K_t]Z_g\begin{bmatrix} M\_b & 0 \\ 0 & M\_w \end{bmatrix} \begin{bmatrix} \ddot{X}\_{body} \\ \ddot{Z}\_w \end{bmatrix} + \begin{bmatrix} -A C\_s H \\ C\_s H \end{bmatrix} \dot{X} + \begin{bmatrix} -A K\_s H \\ K\_s H + K\_t E \end{bmatrix} X = \begin{bmatrix} 0 \\ K\_t \end{bmatrix} Z\_g$
  - $\begin{bmatrix} m\_b & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & I\_p & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & I\_r & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & m\_{wA} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & m\_{wB} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & m\_{wC} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & m\_{wD} \end{bmatrix} \begin{bmatrix} \ddot{z}\_b \\ \ddot{\theta}\_b \\ \ddot{\phi} \\ \ddot{z}\_{wA} \\ \ddot{z}\_{wB} \\ \ddot{z}\_{wC} \\ \ddot{z}\_{wD} \end{bmatrix}\\ + \begin{bmatrix} C\_{11} & C\_{12} & C\_{13} & C\_{14} & C\_{15} & C\_{16} & C\_{17} \\ C\_{21} & C\_{22} & C\_{23} & C\_{24} & C\_{25} & C\_{26} & C\_{27} \\ C\_{31} & C\_{32} & C\_{33} & C\_{34} & C\_{35} & C\_{36} & C\_{37} \\ C\_{41} & C\_{42} & C\_{43} & C\_{44} & C\_{45} & C\_{46} & C\_{47} \\ C\_{51} & C\_{52} & C\_{53} & C\_{54} & C\_{55} & C\_{56} & C\_{57} \\ C\_{61} & C\_{62} & C\_{63} & C\_{64} & C\_{65} & C\_{66} & C\_{67} \\ C\_{71} & C\_{72} & C\_{73} & C\_{74} & C\_{75} & C\_{76} & C\_{77} \end{bmatrix} \begin{bmatrix} \dot{z}\_b \\ \dot{\theta}\_b \\ \dot{\phi} \\ \dot{z}\_{wA} \\ \dot{z}\_{wB} \\ \dot{z}\_{wC} \\ \dot{z}\_{wD} \end{bmatrix} + \begin{bmatrix} K\_{11} & K\_{12} & K\_{13} & K\_{14} & K\_{15} & K\_{16} & K\_{17} \\ K\_{21} & K\_{22} & K\_{23} & K\_{24} & K\_{25} & K\_{26} & K\_{27} \\ K\_{31} & K\_{32} & K\_{33} & K\_{34} & K\_{35} & K\_{36} & K\_{37} \\ K\_{41} & K\_{42} & K\_{43} & K\_{44} & K\_{45} & K\_{46} & K\_{47} \\ K\_{51} & K\_{52} & K\_{53} & K\_{54} & K\_{55} & K\_{56} & K\_{57} \\ K\_{61} & K\_{62} & K\_{63} & K\_{64} & K\_{65} & K\_{66} & K\_{67} \\ K\_{71} & K\_{72} & K\_{73} & K\_{74} & K\_{75} & K\_{76} & K\_{77} \end{bmatrix} \begin{bmatrix} z\_b \\ \theta\_b \\ \phi \\ z\_{wA} \\ z\_{wB} \\ z\_{wC} \\ z\_{wD} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ k\_{tA}z\_{gA} \\ k\_{tB}z\_{gB} \\ k\_{tC}z\_{gC} \\ k\_{tD}z\_{gD} \end{bmatrix}$
  - 状态向量： $X\_{body} = \begin{bmatrix} z\_b \\ \theta\_b \\ \phi \end{bmatrix} % 车轮运动状态向量 Z\_w = \begin{bmatrix} z\_{wA} \\ z\_{wB} \\ z\_{wC} \\ z\_{wD} \end{bmatrix} % 完整状态向量 X = \begin{bmatrix} X\_{body} \\ Z\_w \end{bmatrix} = \begin{bmatrix} z\_b \\ \theta\_b \\ \phi \\ z\_{wA} \\ z\_{wB} \\ z\_{wC} \\ z\_{wD} \end{bmatrix} % 路面激励向量 Z\_g = \begin{bmatrix} z\_{gA} \\ z\_{gB} \\ z\_{gC} \\ z\_{gD} \end{bmatrix}$
  - 几何关系矩阵： $B_f2 1 a −B_f2 1 −b B_r2 1 −b −B_r2]H = \begin{bmatrix} 1 & a & \frac{B\_f}{2} \\ 1 & a & -\frac{B\_f}{2} \\ 1 & -b & \frac{B\_r}{2} \\ 1 & -b & -\frac{B\_r}{2} \end{bmatrix}$
  - 力转换矩阵： $B_f2 −B_f2 B_r2 −B_r2]A = H^T = \begin{bmatrix} 1 & 1 & 1 & 1 \\ a & a & -b & -b \\ \frac{B\_f}{2} & -\frac{B\_f}{2} & \frac{B\_r}{2} & -\frac{B\_r}{2} \end{bmatrix}$
  - 质量矩阵： $M_b = [m_b 0 0 0 I_p 0 0 0 I_r],M_w = [m_wA 0 0 0 0 m_wB 0 0 0 0 m_wC 0 0 0 0 m_wD]M\_b = \begin{bmatrix} m\_b & 0 & 0 \\ 0 & I\_p & 0 \\ 0 & 0 & I\_r \end{bmatrix}, \quad M\_w = \begin{bmatrix} m\_{wA} & 0 & 0 & 0 \\ 0 & m\_{wB} & 0 & 0 \\ 0 & 0 & m\_{wC} & 0 \\ 0 & 0 & 0 & m\_{wD} \end{bmatrix}$
  - 悬架阻尼和刚度矩阵： $C_s = [C_sA 0 0 0 0 C_sB 0 0 0 0 C_sC 0 0 0 0 C_sD],K_s = [k_sA 0 0 0 0 k_sB 0 0 0 0 k_sC 0 0 0 0 k_sD]C\_s = \begin{bmatrix} C\_{sA} & 0 & 0 & 0 \\ 0 & C\_{sB} & 0 & 0 \\ 0 & 0 & C\_{sC} & 0 \\ 0 & 0 & 0 & C\_{sD} \end{bmatrix}, \quad K\_s = \begin{bmatrix} k\_{sA} & 0 & 0 & 0 \\ 0 & k\_{sB} & 0 & 0 \\ 0 & 0 & k\_{sC} & 0 \\ 0 & 0 & 0 & k\_{sD} \end{bmatrix}$
  - 轮胎刚度矩阵： $K_t = [k_tA 0 0 0 0 k_tB 0 0 0 0 k_tC 0 0 0 0 k_tD]K\_t = \begin{bmatrix} k\_{tA} & 0 & 0 & 0 \\ 0 & k\_{tB} & 0 & 0 \\ 0 & 0 & k\_{tC} & 0 \\ 0 & 0 & 0 & k\_{tD} \end{bmatrix}$
- 加主动控制力U的化简详细形式： $K′_t Z_g + RUM\ddot{X} + C\dot{X} + KX = K'\_t Z\_g + RU$ （其中 $U$ 是主动控制力向量，R是控制力分布矩阵）
  - $−I_4]=[1 1 1 1 −a −a b b −B_f2 B_f2 −B_r2 B_r2 −1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1]R = \begin{bmatrix} A \\ -I\_4 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ -a & -a & b & b \\ -\frac{B\_f}{2} & \frac{B\_f}{2} & -\frac{B\_r}{2} & \frac{B\_r}{2} \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}$ 前三行表示控制力对车身三个自由度的影响，后四行表示控制力对四个车轮自由度的影响
  - $KaTeX parse error: Undefined control sequence: \* at position 669: …bmatrix} =K'\_t\̲*̲\begin{bmatrix}…$
    - $K′_t = [0 0 0 0 0 0 0 0 0 0 0 0 k_tA 0 0 0 0 k_tB 0 0 0 0 k_tC 0 0 0 0 k_tD]K'\_t = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ k\_{tA} & 0 & 0 & 0 \\ 0 & k\_{tB} & 0 & 0 \\ 0 & 0 & k\_{tC} & 0 \\ 0 & 0 & 0 & k\_{tD} \end{bmatrix}$
    - $−I_4]=[1 1 1 1 −a −a b b −B_f2 B_f2 −B_r2 B_r2 −1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1]R = \begin{bmatrix} A \\ -I\_4 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ -a & -a & b & b \\ -\frac{B\_f}{2} & \frac{B\_f}{2} & -\frac{B\_r}{2} & \frac{B\_r}{2} \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}$
    - $\begin{aligned} &C\_{11} = -(C\_{sA} + C\_{sB} + C\_{sC} + C\_{sD}) \\ &C\_{12} = -a(C\_{sA} + C\_{sB}) + b(C\_{sC} + C\_{sD}) \\ &C\_{13} = -\frac{B\_f}{2}(C\_{sA} - C\_{sB}) - \frac{B\_r}{2}(C\_{sC} - C\_{sD}) \\ &C\_{14} = C\_{sA}, \quad C\_{15} = C\_{sB}, \quad C\_{16} = C\_{sC}, \quad C\_{17} = C\_{sD} \\ \\ &C\_{21} = -a(C\_{sA} + C\_{sB}) + b(C\_{sC} + C\_{sD}) \\ &C\_{22} = -(a^2C\_{sA} + a^2C\_{sB} + b^2C\_{sC} + b^2C\_{sD}) \\ &C\_{23} = -a\frac{B\_f}{2}C\_{sA} + a\frac{B\_f}{2}C\_{sB} + b\frac{B\_r}{2}C\_{sC} - b\frac{B\_r}{2}C\_{sD} \\ &C\_{24} = aC\_{sA}, \quad C\_{25} = aC\_{sB}, \quad C\_{26} = -bC\_{sC}, \quad C\_{27} = -bC\_{sD} \\ \\ &C\_{31} = -\frac{B\_f}{2}C\_{sA} + \frac{B\_f}{2}C\_{sB} - \frac{B\_r}{2}C\_{sC} + \frac{B\_r}{2}C\_{sD} \\ &C\_{32} = -a\frac{B\_f}{2}C\_{sA} + a\frac{B\_f}{2}C\_{sB} + b\frac{B\_r}{2}C\_{sC} - b\frac{B\_r}{2}C\_{sD} \\ &C\_{33} = -\left\[\left(\frac{B\_f}{2}\right)^2C\_{sA} + \left(\frac{B\_f}{2}\right)^2C\_{sB} + \left(\frac{B\_r}{2}\right)^2C\_{sC} + \left(\frac{B\_r}{2}\right)^2C\_{sD}\right\] \\ &C\_{34} = \frac{B\_f}{2}C\_{sA}, \quad C\_{35} = -\frac{B\_f}{2}C\_{sB}, \quad C\_{36} = \frac{B\_r}{2}C\_{sC}, \quad C\_{37} = -\frac{B\_r}{2}C\_{sD} \\ \\ &C\_{41} = -C\_{sA}, \quad C\_{42} = -aC\_{sA}, \quad C\_{43} = -\frac{B\_f}{2}C\_{sA} \\ &C\_{44} = C\_{sA}, \quad C\_{45} = C\_{46} = C\_{47} = 0 \\ \\ &C\_{51} = -C\_{sB}, \quad C\_{52} = -aC\_{sB}, \quad C\_{53} = \frac{B\_f}{2}C\_{sB} \\ &C\_{54} = 0, \quad C\_{55} = C\_{sB}, \quad C\_{56} = C\_{57} = 0 \\ \\ &C\_{61} = -C\_{sC}, \quad C\_{62} = bC\_{sC}, \quad C\_{63} = -\frac{B\_r}{2}C\_{sC} \\ &C\_{64} = C\_{65} = 0, \quad C\_{66} = C\_{sC}, \quad C\_{67} = 0 \\ \\ &C\_{71} = -C\_{sD}, \quad C\_{72} = bC\_{sD}, \quad C\_{73} = \frac{B\_r}{2}C\_{sD} \\ &C\_{74} = C\_{75} = C\_{76} = 0, \quad C\_{77} = C\_{sD} \end{aligned}$
  - $\begin{aligned} &K\_{11} = -(k\_{sA} + k\_{sB} + k\_{sC} + k\_{sD}) \\ &K\_{12} = -a(k\_{sA} + k\_{sB}) + b(k\_{sC} + k\_{sD}) \\ &K\_{13} = -\frac{B\_f}{2}(k\_{sA} - k\_{sB}) - \frac{B\_r}{2}(k\_{sC} - k\_{sD}) \\ &K\_{14} = k\_{sA}, \quad K\_{15} = k\_{sB}, \quad K\_{16} = k\_{sC}, \quad K\_{17} = k\_{sD} \\ \\ &K\_{21} = -a(k\_{sA} + k\_{sB}) + b(k\_{sC} + k\_{sD}) \\ &K\_{22} = -(a^2k\_{sA} + a^2k\_{sB} + b^2k\_{sC} + b^2k\_{sD}) \\ &K\_{23} = -a\frac{B\_f}{2}k\_{sA} + a\frac{B\_f}{2}k\_{sB} + b\frac{B\_r}{2}k\_{sC} - b\frac{B\_r}{2}k\_{sD} \\ &K\_{24} = ak\_{sA}, \quad K\_{25} = ak\_{sB}, \quad K\_{26} = -bk\_{sC}, \quad K\_{27} = -bk\_{sD} \\ \\ &K\_{31} = -\frac{B\_f}{2}k\_{sA} + \frac{B\_f}{2}k\_{sB} - \frac{B\_r}{2}k\_{sC} + \frac{B\_r}{2}k\_{sD} \\ &K\_{32} = -a\frac{B\_f}{2}k\_{sA} + a\frac{B\_f}{2}k\_{sB} + b\frac{B\_r}{2}k\_{sC} - b\frac{B\_r}{2}k\_{sD} \\ &K\_{33} = -\left\[\left(\frac{B\_f}{2}\right)^2k\_{sA} + \left(\frac{B\_f}{2}\right)^2k\_{sB} + \left(\frac{B\_r}{2}\right)^2k\_{sC} + \left(\frac{B\_r}{2}\right)^2k\_{sD}\right\] \\ &K\_{34} = \frac{B\_f}{2}k\_{sA}, \quad K\_{35} = -\frac{B\_f}{2}k\_{sB}, \quad K\_{36} = \frac{B\_r}{2}k\_{sC}, \quad K\_{37} = -\frac{B\_r}{2}k\_{sD} \\ \\ &K\_{41} = -k\_{sA}, \quad K\_{42} = -ak\_{sA}, \quad K\_{43} = -\frac{B\_f}{2}k\_{sA} \\ &K\_{44} = k\_{sA} + k\_{tA}, \quad K\_{45} = K\_{46} = K\_{47} = 0 \\ \\ &K\_{51} = -k\_{sB}, \quad K\_{52} = -ak\_{sB}, \quad K\_{53} = \frac{B\_f}{2}k\_{sB} \\ &K\_{54} = 0, \quad K\_{55} = k\_{sB} + k\_{tB}, \quad K\_{56} = K\_{57} = 0 \\ \\ &K\_{61} = -k\_{sC}, \quad K\_{62} = bk\_{sC}, \quad K\_{63} = -\frac{B\_r}{2}k\_{sC} \\ &K\_{64} = K\_{65} = 0, \quad K\_{66} = k\_{sC} + k\_{tC}, \quad K\_{67} = 0 \\ \\ &K\_{71} = -k\_{sD}, \quad K\_{72} = bk\_{sD}, \quad K\_{73} = \frac{B\_r}{2}k\_{sD} \\ &K\_{74} = K\_{75} = K\_{76} = 0, \quad K\_{77} = k\_{sD} + k\_{tD} \end{aligned}$ 解耦
  - 此方程为CDC（连续阻尼控制）或主动悬架控制算法设计的基础，通过调节控制力 UU 可以优化车辆平顺性、操控性和稳定性。

代码：

import numpy as np
import scipy.linalg as la
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

class SevenDOFVehicle:
    """七自由度车辆悬架系统模型"""
    
    def __init__(self):
        """初始化车辆参数"""
        # 簧载质量参数
        self.m_b = 800.0      # 簧载质量 (kg)
        self.I_p = 310.0      # 俯仰转动惯量 (kg·m²)
        self.I_r = 1060.0     # 侧倾转动惯量 (kg·m²)
        
        # 几何参数
        self.a = 1.13         # 前轴到质心距离 (m)
        self.b = 1.21         # 后轴到质心距离 (m)
        self.B1 = 1.3         # 轮距 (m)
        self.half_B = self.B1 / 2.0
        
        # 非簧载质量
        self.m_wA = 26.5      # 左前轮质量 (kg)
        self.m_wB = 26.5      # 右前轮质量 (kg)
        self.m_wC = 24.4      # 左后轮质量 (kg)
        self.m_wD = 24.4      # 右后轮质量 (kg)
        
        # 悬架刚度
        self.K_sf1 = 20600.0  # 前悬架刚度1 (N/m)
        self.K_sf2 = 30060.0  # 前悬架刚度2 (N/m)
        self.K_sr1 = 15200.0  # 后悬架刚度1 (N/m)
        self.K_sr2 = 20520.0  # 后悬架刚度2 (N/m)
        
        # 悬架阻尼
        self.C_sf1 = 1670.0   # 前悬架阻尼1 (N·s/m)
        self.C_sf2 = 750.0    # 前悬架阻尼2 (N·s/m)
        self.C_sr1 = 1660.0   # 后悬架阻尼1 (N·s/m)
        self.C_sr2 = 900.0    # 后悬架阻尼2 (N·s/m)
        
        # 轮胎刚度
        self.K_tf = 138000.0  # 前轮胎刚度 (N/m)
        self.K_tr = 138000.0  # 后轮胎刚度 (N/m)，假设与前轮相同
        
        # 车速
        self.v = 50.0         # 车速 (km/h)
        self.v_ms = self.v / 3.6  # 转换为m/s
        
        # 状态维度
        self.n_dof = 7        # 自由度数量
        
        # 构建系统矩阵
        self.build_system_matrices()
        
        # 模态分析
        self.perform_modal_analysis()
        
        # 设计天棚阻尼控制器
        self.design_skyhook_controller()
    
    def build_system_matrices(self):
        """构建系统质量、刚度、阻尼矩阵"""
        # 质量矩阵 M (对角矩阵)
        self.M = np.diag([self.m_b, self.I_p, self.I_r, 
                          self.m_wA, self.m_wB, self.m_wC, self.m_wD])
        
        # 刚度矩阵 K
        self.K = np.zeros((self.n_dof, self.n_dof))
        
        # 对角元素
        # 车身垂直刚度：四个悬架刚度之和
        K_vert = (self.K_sf1 + self.K_sf2 + self.K_sr1 + self.K_sr2)
        
        # 俯仰刚度
        K_pitch = (self.K_sf1 + self.K_sf2) * self.a**2 + (self.K_sr1 + self.K_sr2) * self.b**2
        
        # 侧倾刚度
        K_roll = (self.K_sf1 + self.K_sr1) * self.half_B**2 + (self.K_sf2 + self.K_sr2) * self.half_B**2
        
        # 车轮垂直刚度
        K_wA = self.K_sf1 + self.K_tf  # 左前轮
        K_wB = self.K_sf2 + self.K_tf  # 右前轮
        K_wC = self.K_sr1 + self.K_tr  # 左后轮
        K_wD = self.K_sr2 + self.K_tr  # 右后轮
        
        self.K[0, 0] = K_vert
        self.K[1, 1] = K_pitch
        self.K[2, 2] = K_roll
        self.K[3, 3] = K_wA
        self.K[4, 4] = K_wB
        self.K[5, 5] = K_wC
        self.K[6, 6] = K_wD
        
        # 耦合项
        # 车身垂直-俯仰耦合
        self.K[0, 1] = self.K[1, 0] = (self.K_sf1 + self.K_sf2) * self.a - (self.K_sr1 + self.K_sr2) * self.b
        
        # 车身垂直-侧倾耦合
        self.K[0, 2] = self.K[2, 0] = (self.K_sf1 - self.K_sf2 + self.K_sr1 - self.K_sr2) * self.half_B
        
        # 车身垂直-车轮耦合
        self.K[0, 3] = self.K[3, 0] = -self.K_sf1  # 左前
        self.K[0, 4] = self.K[4, 0] = -self.K_sf2  # 右前
        self.K[0, 5] = self.K[5, 0] = -self.K_sr1  # 左后
        self.K[0, 6] = self.K[6, 0] = -self.K_sr2  # 右后
        
        # 俯仰-侧倾耦合
        self.K[1, 2] = self.K[2, 1] = (self.K_sf1 - self.K_sf2) * self.a * self.half_B - \
                                      (self.K_sr1 - self.K_sr2) * self.b * self.half_B
        
        # 俯仰-车轮耦合
        self.K[1, 3] = self.K[3, 1] = -self.a * self.K_sf1  # 左前
        self.K[1, 4] = self.K[4, 1] = -self.a * self.K_sf2  # 右前
        self.K[1, 5] = self.K[5, 1] = self.b * self.K_sr1   # 左后
        self.K[1, 6] = self.K[6, 1] = self.b * self.K_sr2   # 右后
        
        # 侧倾-车轮耦合
        self.K[2, 3] = self.K[3, 2] = -self.half_B * self.K_sf1  # 左前
        self.K[2, 4] = self.K[4, 2] = self.half_B * self.K_sf2   # 右前
        self.K[2, 5] = self.K[5, 2] = -self.half_B * self.K_sr1  # 左后
        self.K[2, 6] = self.K[6, 2] = self.half_B * self.K_sr2   # 右后
        
        # 阻尼矩阵 C (结构与刚度矩阵类似)
        self.C = np.zeros((self.n_dof, self.n_dof))
        
        # 对角元素
        C_vert = (self.C_sf1 + self.C_sf2 + self.C_sr1 + self.C_sr2)
        C_pitch = (self.C_sf1 + self.C_sf2) * self.a**2 + (self.C_sr1 + self.C_sr2) * self.b**2
        C_roll = (self.C_sf1 + self.C_sr1) * self.half_B**2 + (self.C_sf2 + self.C_sr2) * self.half_B**2
        
        self.C[0, 0] = C_vert
        self.C[1, 1] = C_pitch
        self.C[2, 2] = C_roll
        self.C[3, 3] = self.C_sf1  # 左前轮
        self.C[4, 4] = self.C_sf2  # 右前轮
        self.C[5, 5] = self.C_sr1  # 左后轮
        self.C[6, 6] = self.C_sr2  # 右后轮
        
        # 耦合项（与刚度矩阵相同的模式）
        # 车身垂直-俯仰耦合
        self.C[0, 1] = self.C[1, 0] = (self.C_sf1 + self.C_sf2) * self.a - (self.C_sr1 + self.C_sr2) * self.b
        
        # 车身垂直-侧倾耦合
        self.C[0, 2] = self.C[2, 0] = (self.C_sf1 - self.C_sf2 + self.C_sr1 - self.C_sr2) * self.half_B
        
        # 车身垂直-车轮耦合
        self.C[0, 3] = self.C[3, 0] = -self.C_sf1
        self.C[0, 4] = self.C[4, 0] = -self.C_sf2
        self.C[0, 5] = self.C[5, 0] = -self.C_sr1
        self.C[0, 6] = self.C[6, 0] = -self.C_sr2
        
        # 俯仰-侧倾耦合
        self.C[1, 2] = self.C[2, 1] = (self.C_sf1 - self.C_sf2) * self.a * self.half_B - \
                                      (self.C_sr1 - self.C_sr2) * self.b * self.half_B
        
        # 俯仰-车轮耦合
        self.C[1, 3] = self.C[3, 1] = -self.a * self.C_sf1
        self.C[1, 4] = self.C[4, 1] = -self.a * self.C_sf2
        self.C[1, 5] = self.C[5, 1] = self.b * self.C_sr1
        self.C[1, 6] = self.C[6, 1] = self.b * self.C_sr2
        
        # 侧倾-车轮耦合
        self.C[2, 3] = self.C[3, 2] = -self.half_B * self.C_sf1
        self.C[2, 4] = self.C[4, 2] = self.half_B * self.C_sf2
        self.C[2, 5] = self.C[5, 2] = -self.half_B * self.C_sr1
        self.C[2, 6] = self.C[6, 2] = self.half_B * self.C_sr2
        
        # 控制矩阵 R (7x4)
        # 四个控制力分别作用在四个悬架上
        self.R = np.zeros((self.n_dof, 4))
        
        # 控制力u_sA（左前悬架）
        self.R[0, 0] = 1.0                    # 影响车身垂直位移
        self.R[1, 0] = -self.a               # 影响俯仰（负号是因为左前在质心前方）
        self.R[2, 0] = -self.half_B          # 影响侧倾（负号是因为在左侧）
        self.R[3, 0] = -1.0                  # 影响左前轮位移
        
        # 控制力u_sB（右前悬架）
        self.R[0, 1] = 1.0
        self.R[1, 1] = -self.a
        self.R[2, 1] = self.half_B           # 正号是因为在右侧
        self.R[4, 1] = -1.0                  # 影响右前轮位移
        
        # 控制力u_sC（左后悬架）
        self.R[0, 2] = 1.0
        self.R[1, 2] = self.b                # 正号是因为在质心后方
        self.R[2, 2] = -self.half_B
        self.R[5, 2] = -1.0                  # 影响左后轮位移
        
        # 控制力u_sD（右后悬架）
        self.R[0, 3] = 1.0
        self.R[1, 3] = self.b
        self.R[2, 3] = self.half_B
        self.R[6, 3] = -1.0                  # 影响右后轮位移
        
        # 路面激励输入矩阵 K_t (7x4)
        self.K_t = np.zeros((self.n_dof, 4))
        self.K_t[3, 0] = self.K_tf  # 左前轮路面输入
        self.K_t[4, 1] = self.K_tf  # 右前轮路面输入
        self.K_t[5, 2] = self.K_tr  # 左后轮路面输入
        self.K_t[6, 3] = self.K_tr  # 右后轮路面输入
    
    def perform_modal_analysis(self):
        """执行模态分析，得到主振型矩阵"""
        # 求解无阻尼自由振动特征值问题: K * φ = ω² * M * φ
        eigvals, eigvecs = la.eigh(self.K, self.M)
        
        # 特征值按升序排列，特征向量对应排列
        idx = eigvals.argsort()
        self.eigenvalues = eigvals[idx] # 按相同的顺序重新排列特征向量列
        self.Q = eigvecs[:, idx]  # 主振型矩阵
        
        # 计算固有频率 (Hz)
        self.natural_freqs = np.sqrt(self.eigenvalues) / (2 * np.pi)
        
        # 质量归一化 (使模态质量为1)
        for i in range(self.n_dof):
            modal_mass = self.Q[:, i].T @ self.M @ self.Q[:, i]
            self.Q[:, i] = self.Q[:, i] / np.sqrt(modal_mass)
        
        # 验证正交性
        self.M_bar = self.Q.T @ self.M @ self.Q  # 应该接近单位矩阵
        self.K_bar = self.Q.T @ self.K @ self.Q  # 应该是对角矩阵（特征值矩阵）
        self.C_bar = self.Q.T @ self.C @ self.Q  # 通常不是对角矩阵
        
        # 提取阻尼矩阵的对角和非对角部分
        self.C_di = np.diag(np.diag(self.C_bar))  # 对角部分
        self.C_p = self.C_bar - self.C_di         # 非对角部分
    
    def design_skyhook_controller(self):
        """设计天棚阻尼控制器"""
        # 计算每个模态的天棚阻尼系数（临界阻尼条件）
        self.c_sky = np.zeros(self.n_dof)
        
        for i in range(self.n_dof):
            m_i = self.M_bar[i, i]        # 模态质量
            k_i = self.K_bar[i, i]        # 模态刚度
            c_di = self.C_di[i, i]        # 模态固有阻尼
            
            # 临界阻尼系数：2 * sqrt(m_i * k_i)
            c_critical = 2 * np.sqrt(m_i * k_i)
            
            # 天棚阻尼系数 = 临界阻尼 - 固有阻尼
            self.c_sky[i] = max(0, c_critical - c_di)
        
        # 天棚阻尼矩阵
        self.C_sky = np.diag(self.c_sky)
        
        # 计算控制力变换矩阵
        # 根据公式: U = (Q^T R)^{-1} Q^{-1} (C_sky + C_p) \dot{X}
        # 注意: Q^T R 是7x4矩阵，不是方阵，需要求广义逆
        
        # 计算 Q 的逆矩阵
        Q_inv = la.inv(self.Q)
        
        # 计算 Q^T R
        QTR = self.Q.T @ self.R
        
        # 计算广义逆 (Moore-Penrose伪逆)
        QTR_pinv = la.pinv(QTR)
        
        # 总变换矩阵
        self.control_gain = QTR_pinv @ Q_inv @ (self.C_sky + self.C_p)
        
        # 检查矩阵维度
        print(f"控制增益矩阵维度: {self.control_gain.shape}")
        print(f"期望维度: (4, 7) - 4个控制力，7个状态速度")
    
    def calculate_control_force(self, dX):
        """计算控制力
        dX: 状态向量的一阶导数 (7维向量)
        返回: 四个控制力 u_sA, u_sB, u_sC, u_sD
        """
        # U = control_gain * dX
        U = self.control_gain @ dX
        return U
    
    def road_excitation(self, t, road_type="random"):
        """生成路面激励
        t: 时间 (s)
        road_type: 路面类型 ('random', 'bump', 'sine')
        返回: 四个车轮的路面位移 (m)
        """
        if road_type == "random":
            # 随机路面激励（简化白噪声）
            np.random.seed(int(t*1000) % 10000)
            Z_g = 0.01 * np.random.randn(4)
            
        elif road_type == "bump":
            # 单个凸起
            bump_time = 0.5  # 凸起时间
            bump_height = 0.05  # 凸起高度
            
            if 0.4 < t < 0.6:
                # 所有车轮同时经过凸起
                Z_g = bump_height * np.sin(np.pi * (t - 0.4) / 0.2) * np.ones(4)
            else:
                Z_g = np.zeros(4)
                
        elif road_type == "sine":
            # 正弦波路面
            freq = 2.0  # Hz
            amplitude = 0.02  # m
            
            # 考虑前后轮的时间延迟
            wheelbase = self.a + self.b
            time_delay = wheelbase / self.v_ms
            
            Z_g = np.zeros(4)
            # 前轮
            Z_g[0] = amplitude * np.sin(2 * np.pi * freq * t)
            Z_g[1] = amplitude * np.sin(2 * np.pi * freq * t)
            # 后轮（有时间延迟）
            Z_g[2] = amplitude * np.sin(2 * np.pi * freq * (t - time_delay))
            Z_g[3] = amplitude * np.sin(2 * np.pi * freq * (t - time_delay))
        
        return Z_g
    
    def vehicle_dynamics(self, t, state, active_control=True, road_type="random"):
        """车辆动力学方程
        state: [Z_b, θ, ψ, Z_wA, Z_wB, Z_wC, Z_wD, 
                dZ_b, dθ, dψ, dZ_wA, dZ_wB, dZ_wC, dZ_wD]
        返回: 状态导数
        """
        # 分离位移和速度
        X = state[:self.n_dof]
        dX = state[self.n_dof:]
        
        # 路面激励
        Z_g = self.road_excitation(t, road_type)
        
        # 计算控制力
        if active_control:
            U = self.calculate_control_force(dX)
        else:
            U = np.zeros(4)  # 被动悬架
        
        # 计算加速度: M * ddX = K_t * Z_g + R * U - C * dX - K * X
        # 整理得: ddX = M^{-1} * (K_t * Z_g + R * U - C * dX - K * X)
        # 牛顿第二定律
        forces = self.K_t @ Z_g + self.R @ U - self.C @ dX - self.K @ X
        ddX = la.solve(self.M, forces)
        
        # 返回状态导数
        return np.concatenate([dX, ddX])
    
    def simulate(self, t_span=(0, 5), dt=0.001, active_control=True, road_type="random"):
        """运行仿真"""
        # 初始状态（静止）
        initial_state = np.zeros(2 * self.n_dof)
        
        # 时间点
        t_eval = np.arange(t_span[0], t_span[1], dt)
        
        # 求解ODE -- 求解车辆动力学微分方程的数值解
        sol = solve_ivp(
            lambda t, y: self.vehicle_dynamics(t, y, active_control, road_type),
            t_span,
            initial_state,
            t_eval=t_eval,
            method='RK45',
            rtol=1e-6,
            atol=1e-9
        )
        
        return sol.t, sol.y
    
    def plot_results(self, t, y, title="车辆悬架响应"):
        """绘制仿真结果"""
        fig, axes = plt.subplots(4, 2, figsize=(12, 10))
        fig.suptitle(title, fontsize=16)
        
        # 车身垂直位移
        axes[0, 0].plot(t, y[0, :])
        axes[0, 0].set_ylabel('车身垂直位移 (m)')
        axes[0, 0].grid(True)
        
        # 车身俯仰角
        axes[0, 1].plot(t, y[1, :])
        axes[0, 1].set_ylabel('俯仰角 (rad)')
        axes[0, 1].grid(True)
        
        # 车身侧倾角
        axes[1, 0].plot(t, y[2, :])
        axes[1, 0].set_ylabel('侧倾角 (rad)')
        axes[1, 0].grid(True)
        
        # 左前轮位移
        axes[1, 1].plot(t, y[3, :])
        axes[1, 1].set_ylabel('左前轮位移 (m)')
        axes[1, 1].grid(True)
        
        # 右前轮位移
        axes[2, 0].plot(t, y[4, :])
        axes[2, 0].set_ylabel('右前轮位移 (m)')
        axes[2, 0].grid(True)
        
        # 左后轮位移
        axes[2, 1].plot(t, y[5, :])
        axes[2, 1].set_ylabel('左后轮位移 (m)')
        axes[2, 1].grid(True)
        
        # 右后轮位移
        axes[3, 0].plot(t, y[6, :])
        axes[3, 0].set_ylabel('右后轮位移 (m)')
        axes[3, 0].set_xlabel('时间 (s)')
        axes[3, 0].grid(True)
        
        # 车身垂直加速度
        d2Z_b = np.gradient(y[7, :], t)  # 对速度微分得到加速度
        axes[3, 1].plot(t, d2Z_b)
        axes[3, 1].set_ylabel('车身垂直加速度 (m/s²)')
        axes[3, 1].set_xlabel('时间 (s)')
        axes[3, 1].grid(True)
        
        plt.tight_layout()
        plt.show()
    
    def print_system_info(self):
        """打印系统信息"""
        print("=" * 60)
        print("七自由度车辆悬架系统")
        print("=" * 60)
        
        print("\n1. 系统参数:")
        print(f"   簧载质量 m_b = {self.m_b} kg")
        print(f"   俯仰转动惯量 I_p = {self.I_p} kg·m²")
        print(f"   侧倾转动惯量 I_r = {self.I_r} kg·m²")
        print(f"   前轴到质心距离 a = {self.a} m")
        print(f"   后轴到质心距离 b = {self.b} m")
        print(f"   轮距 B1 = {self.B1} m")
        
        print("\n2. 模态分析结果:")
        print("   固有频率 (Hz):")
        for i, freq in enumerate(self.natural_freqs):
            print(f"     模态 {i+1}: {freq:.3f} Hz")
        
        print("\n3. 天棚阻尼系数:")
        for i, c in enumerate(self.c_sky):
            print(f"     模态 {i+1}: {c:.2f} N·s/m")
        
        print("\n4. 控制增益矩阵维度:", self.control_gain.shape)
        print("=" * 60)


# 主程序
def main():
    """主程序：运行仿真并比较主动和被动悬架"""
    # 创建车辆模型
    vehicle = SevenDOFVehicle()
    vehicle.print_system_info()
    
    print("\n正在运行仿真...")
    
    # 仿真1：被动悬架（无控制）
    print("\n1. 被动悬架仿真...")
    t_passive, y_passive = vehicle.simulate(
        t_span=(0, 3),
        dt=0.001,
        active_control=False,
        road_type="sine"
    )
    
    # 仿真2：主动悬架（模态解耦天棚阻尼控制）
    print("2. 主动悬架仿真...")
    t_active, y_active = vehicle.simulate(
        t_span=(0, 3),
        dt=0.001,
        active_control=True,
        road_type="sine"
    )
    
    # 绘制比较结果
    fig, axes = plt.subplots(3, 1, figsize=(10, 8))
    
    # 车身垂直位移比较
    axes[0].plot(t_passive, y_passive[0, :], 'b-', label='被动悬架', linewidth=2)
    axes[0].plot(t_active, y_active[0, :], 'r--', label='主动悬架', linewidth=2)
    axes[0].set_ylabel('车身垂直位移 (m)')
    axes[0].legend()
    axes[0].grid(True)
    axes[0].set_title('车身垂直位移响应比较')
    
    # 车身俯仰角比较
    axes[1].plot(t_passive, y_passive[1, :], 'b-', label='被动悬架', linewidth=2)
    axes[1].plot(t_active, y_active[1, :], 'r--', label='主动悬架', linewidth=2)
    axes[1].set_ylabel('俯仰角 (rad)')
    axes[1].legend()
    axes[1].grid(True)
    axes[1].set_title('车身俯仰角响应比较')
    
    # 车身侧倾角比较
    axes[2].plot(t_passive, y_passive[2, :], 'b-', label='被动悬架', linewidth=2)
    axes[2].plot(t_active, y_active[2, :], 'r--', label='主动悬架', linewidth=2)
    axes[2].set_ylabel('侧倾角 (rad)')
    axes[2].set_xlabel('时间 (s)')
    axes[2].legend()
    axes[2].grid(True)
    axes[2].set_title('车身侧倾角响应比较')
    
    plt.tight_layout()
    plt.show()
    
    # 计算性能指标
    def calculate_rms(signal):
        return np.sqrt(np.mean(signal**2))
    
    # 车身垂直加速度RMS
    d2Z_b_passive = np.gradient(y_passive[7, :], t_passive)
    d2Z_b_active = np.gradient(y_active[7, :], t_active)
    
    rms_acc_passive = calculate_rms(d2Z_b_passive)
    rms_acc_active = calculate_rms(d2Z_b_active)
    
    print("\n性能指标比较:")
    print(f"车身垂直加速度RMS值:")
    print(f"  被动悬架: {rms_acc_passive:.4f} m/s²")
    print(f"  主动悬架: {rms_acc_active:.4f} m/s²")
    print(f"  改善幅度: {(1 - rms_acc_active/rms_acc_passive)*100:.1f}%")
    
    # 绘制模态振型
    fig, ax = plt.subplots(figsize=(10, 6))
    for i in range(min(7, 4)):  # 只显示前4个模态
        ax.plot(range(1, 8), vehicle.Q[:, i], 'o-', label=f'模态 {i+1}')
    
    ax.set_xlabel('自由度编号')
    ax.set_ylabel('模态振型幅值')
    ax.set_title('前4阶模态振型')
    ax.legend()
    ax.grid(True)
    plt.xticks(range(1, 8), ['Z_b', 'θ', 'ψ', 'Z_wA', 'Z_wB', 'Z_wC', 'Z_wD'])
    plt.show()


if __name__ == "__main__":
    main()

创建车辆模型
- 初始化
  - 簧载质量、俯仰惯量、侧倾惯量、非簧载质量
  - 几何参数：前轴-质心距离、后轴-质心距离、轮距、半轮距
  - 四个悬架的刚度、四个悬架的阻尼、四个轮胎的刚度
- 构建系统矩阵
  - 质量矩阵M：7*7的对角矩阵
  - 刚度矩阵K：7*7的包含车身-悬架耦合项
  - 阻尼矩阵C：7*7
  - 控制矩阵R：7*4的–4个控制力（悬架）对7个状态的影响
  - 路面激励输入矩阵Kt：7*4的矩阵
- 模态分析：识别系统固有特性，为控制器设计提供依据
  - 求解特征值问题 → 特征值升序排序 → 特征向量对应列交换 → 计算固有频率 → 振型矩阵Q每一列归一化→验证正交性→提取模态参数
- 设计天棚控制器：设计基于模态的天棚阻尼控制器
- 仿真与验证–模拟车辆在路面激励下的动态响应
  - 车辆动力学方程建立：
    - 状态矩阵初始化： $X_body = [z_b θ_b ϕ]X\_{body} = \begin{bmatrix} z\_b \\ \theta\_b \\ \phi \end{bmatrix}$
    - 计算控制力（被动悬架为0，半主动悬架用论文的天棚）
    - F=ma计算簧上加速度向量： $K′_t Z_g + RUM\ddot{X} + C\dot{X} + KX = K'\_t Z\_g + RU$
    - 返回状态向量 $X$ 和 $X¨\ddot{X}$
  - 时间向量生成：
  - 求解ODE方程–车辆动力学微分方程的数值解得到
    - lambda t, y: self.vehicle_dynamics(...) 定义微分方程系统 dy/dt = f(t, y)返回值: 状态导数值（速度 + 加速度）
    - 求解方法：‘RK45’–Runge-Kutta 4/5阶（显式方法）

论文阅读记录

论文名称	论文类型	论文总结
《整车主动悬架系统天棚阻尼控制策略》	期刊	（1）整车悬架是一个多自由度耦合的系统，车身侧倾、俯仰运动与各轮胎垂向运动是相互干涉；带来的问题是如何协调四个控制器的作用力大小使车身始终保持良好的运动姿态；在真实的七自由度悬架系统中，由于悬架连接车身和车轮，系统通常存在耦合：① 几何耦合：车身运动通过悬架传递到四个车轮 ②弹性耦合：一个悬架的变形会影响其他悬架③ 惯性耦合：俯仰和侧倾运动与垂直运动之间存在惯性耦合。→ 表现为刚度矩阵K、阻尼矩阵C、质量矩阵M有非对角元素。（2）本文基于7自由度悬架模型，提出运用模态解耦方法，得到同等数量独立的单模态振动系统，对各个独立的模态振动采用经典的天棚阻尼控制策略，然后将各模态耦合，即可用实际中的四个控制器实现；阻尼矩阵C_bar = CDi + Cp，CDi 是对角矩阵（3）解耦处理：每个模态的稳定性可以单独判断。且当三个矩阵都是对角矩阵时，系统的7个运动方程相互独立，每个方程只描述一个自由度的运动，与其他自由度无关。实现解耦的方式：X= φQ