切比雪夫多项式逼近精度比较

切比雪夫多项式在测量自动化中的应用

摘要

本文比较了使用第一类和第二类九阶切比雪夫多项式复现平方根函数的精度。通过多项式函数在区间[–1; 1]上相对于参考函数的最大正负偏差以及误差曲线下的面积来估计精度。

关键词

information-measuring系统，标准函数，专用计算器。

一、引言

现代数字处理器在硬件层面仅实现简单的算术和逻辑运算，因此需要采用各种方法和计算逼近算法来计算更复杂的函数，例如 sin(x)、log(x)、 √x 等。在计算机技术中的应用中，这些表达式应由处理器可理解的基本算术运算（直接或在其展开式中）构成。

在复现函数关系时，多项式逼近方法得到了广泛应用，该方法常用于各种科学与应用技术问题中：从在现代专用微处理器中逼近标准数学函数，到实现工作标准的校准特性、传感器和测量系统的校准。例如，获取先验未知函数关系的参考值f(x)的繁琐操作，通常通过各种次数的多项式[1‐5]以给定精度进行逼近。多项式方法之所以普遍，是由于其简单性、清晰的几何解释，以及最重要的是，在使用如下形式的多项式计算函数f(x)的值f(x)时具有较低的计算成本

$$
\varphi(x) = a_0 + a_1x + \cdots + a_nx^n = \sum_{k=0}^{n} a_kx^k,
$$

其中 $a_0、a_1、\cdots、a_n$ 是一些常数。

使用霍纳法时，表达式（1）被转换为：

$$
\varphi_n(x) = a_0 + a_1x + \cdots + a_nx^n = (((a_nx + a_{n-1})x + a_{n-2})x + \cdots + a_1)x + a_0.
$$

计算一个n次多项式的计算复杂度为2n次操作：n次乘法和n次加法（n(×) + n(+)）。此外，在内存中需要存储 n+1个常数$a_0,a_1, . . . , a_n$，并在计算多项式时调用它们。

求多项式(1)系数的方法有多种——这是一种基于函数泰勒级数展开的经典方法（关于函数逼近精度的分析在应用于数字信号处理器时可参见[2]），而目前常用的方法则是基于切比雪夫多项式的逼近，特别是采用切比雪夫最佳逼近多项式，此时在逼近区间x∈[a, b]上，误差的n + 2个极值Gi, i ∈0,1, …, n+1的符号交替变化，且绝对值[2],相等，以及其他一些在实践中较少使用的鲜为人知的多项式[6]。

本工作的目的是通过在0到1区间内计算平方根的函数示例，对使用第一类和第二类切比雪夫多项式逼近函数关系时的精度进行比较分析。

II. 函数向正交多项式的分解

在[6],中指出，对于在区间[a；b]上关于权函数ω(x)的正交多项式$f_k(x)$，当m ≠ n时，必须满足以下条件

$$
\int_a^b f_m(x)f_n(x)\omega(x)dx = 0.
$$

由关系式(3)可以看出，通过适当选择权函数ω(x)，可以构造出大量正交函数。

在现有的多种多项式中，最广为人知且在实际数字信号处理器中广泛应用的是切比雪夫多项式。满足(3)式、权函数为 $\omega(x) = \frac{1}{\sqrt{1 - x^2}}$的第一类切比雪夫多项式由递推方程确定

$$
T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)
$$

在$T_0(x) = 1$和$T_1(x) = x$。

)

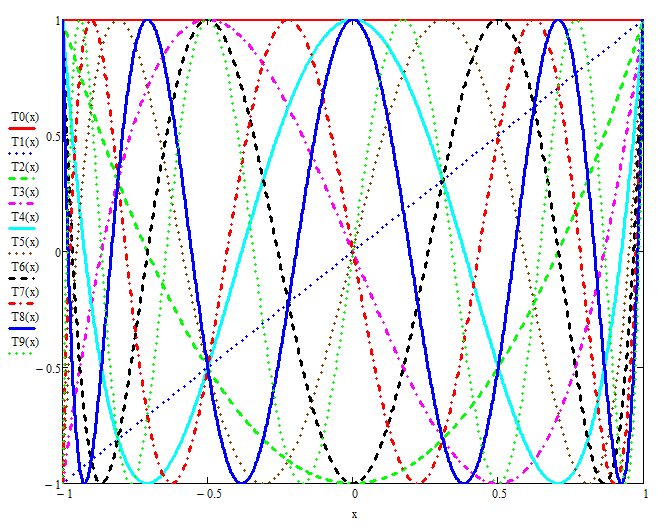
a) 第一类

)

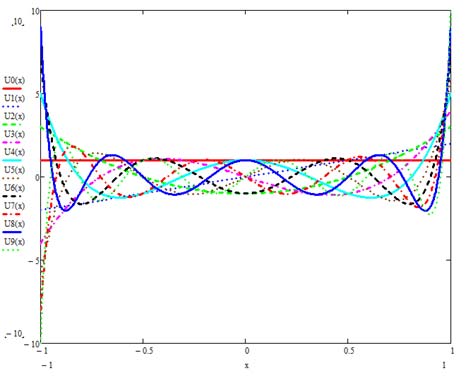
b) 第二类
图1. 切比雪夫多项式

从图1可以看出，对于n的任意取值，在x∈[–1； 1]的区间内，函数$T_n(x)$关于零点对称；它要么是偶函数，要么是奇函数（取决于n）。函数$T_n(x)$的极值符号交替变化，且其绝对值等于1。

第二类切比雪夫多项式 $U_n(x)$ 可在区间 x∈[–1; 1]上利用递推关系定义：

$$
U_{n+1}(x) = 2xU_n(x) - U_{n-1}(x)
$$

在 $U_0(x) = 1$和 $U_1(x) = 2x$。

在图1 b)中给出了前十个第二类切比雪夫多项式变化的曲线图。从图1 b)可以看出，第二类切比雪夫多项式与第一类多项式不同，在边缘处取值较大且为1，但与第一类多项式一样，相对于零对称，且为偶函数或奇函数。

为了求第一类切比雪夫级数的系数，我们必须对a = –1，b = 1和$\omega(x) = 1/\sqrt{1 - x^2}$使用关系式(3)，我们得到

$$
\int_{-1}^{1} T_m(x)T_n(x) \frac{1}{\sqrt{1 - x^2}} dx =
\begin{cases}
0, & m \neq n, \
\pi/2, & m = n > 0, \
\pi, & m = n = 0.
\end{cases}
$$

如果我们把函数f(x)的切比雪夫级数写成如下形式

$$
\varphi(x) = \frac{c_0}{2} + c_1T_1(x) + c_2T_2(x) + \cdots,
$$

将等式(7)的两边同时乘以$\frac{T_n(x)}{\sqrt{1 - x^2}}$，然后在区间[‐1,1]上逐项积分，并利用(6)，我们得到一个用于求级数(7)系数的表达式

$$
c_n = \frac{2}{\pi} \int_{-1}^{1} f(x)T_n(x) \frac{1}{\sqrt{1 - x^2}} dx, \quad n = 0,1,2,\dots
$$

对于第二类切比雪夫多项式，级数(7)的系数由下列表达式求得

$$
c_n = \frac{2}{\pi} \int_{-1}^{1} f(x)U_n(x)\sqrt{1 - x^2}dx, \quad n = 0,1,2,\dots
$$

考虑函数展开

$$
f(x) = \sqrt{x}
$$

在[0, 1]的区间上，使用第一类和第二类切比雪夫多项式进行最高到9阶的逼近。函数逼近的精度将通过两种方法进行评估——逼近区间内的最大误差值以及误差曲线下的面积 [7, 8]的大小。

由于函数的逼近区间不同于切比雪夫多项式展开区间[–1；1], ，因此需要将函数定义区间

$$
[t = \frac{a + b}{2} + \frac{b - a}{2}x, \quad -1 \leq x \leq 1.]
$$

表 I. 逼近函数的最大偏差值（第一类切比雪夫多项式）

阶数 多项式	0	1	2	3	4
G⁺	0.363	0.082	0.046	0.032	0.025
G⁻	0.637	0.212	0.127	0.091	0.071
Sош	0.03	0.05	0.022	0.012	7.98×10⁻³

阶数 多项式	5	6	7	8	9
G⁺	0.02	0.017	0.015	0.013	0.012
G⁻	0.058	0.049	0.042	0.037	0.034
Sош	5.56×10⁻³	4.08×10⁻³	3.13×10⁻³	2.47×10⁻³	2×10⁻³

表 II. 逼近函数的最大偏差值（第二类切比雪夫多项式）

阶数 多项式	0	1	2	3	4
G⁺	0.321	0.031	0.03	0.01	0.011
G⁻	0.679	0.291	0.194	0.107	0.119
Sош	0.196	0.034	0.013	6.3×10⁻³	3.6×10⁻³

阶数 多项式	5	6	7	8	9
G⁺	0.0065	0.0058	0.0048	0.0042	0.0038
G⁻	0.1	0.086	0.076	0.068	0.0085
Sош	2.2×10⁻³	1.6×10⁻³	1.1×10⁻³	8.1×10⁻⁴	6.2×10⁻⁴

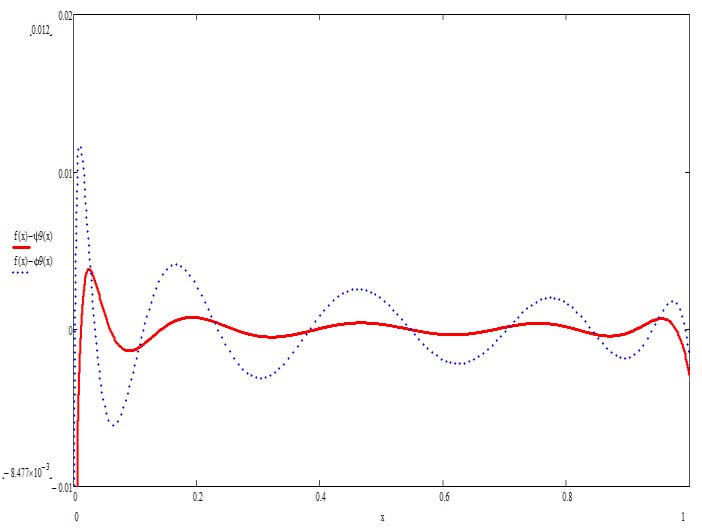
图2. 使用第一类（虚线）和第二类（实线）九阶切比雪夫多项式逼近函数 $f(x) = \sqrt{x}$ 时的逼近误差曲线图

从图2可以看出，误差曲线在逼近区间内相对于零值呈振荡状，最大偏差的值不同，且所得曲线与对应于切比雪夫最佳逼近多项式[2]的误差曲线有显著差异。也就是说，使用多项式(4)进行函数逼近并不能提供可达到的最大逼近精度。

此外，通过比较图2中的曲线可以看出，使用第二类多项式对函数进行逼近的精度高于使用第一类多项式的情况。

从表 I 和表 II 可以看出，随着多项式次数的增加，逼近误差的最大偏差减小，误差曲线下的面积也随之减小。对表 I 和表 II 数值的比较表明，使用第二类多项式对函数进行逼近的精度高于使用第一类切比雪夫多项式时的逼近精度。

III. 结论

所得结果表明如下：
1. 多项式逼近方法允许以任意给定的精度，在某一取值范围内，几乎达到任意精度地表示解析定义的函数；
2. 第一类和第二类切比雪夫多项式可以提供足够高的效率指标，且第二类切比雪夫多项式的逼近精度高于第一类，然而这些多项式仅针对两种特定的权函数得到，其他值的多项式不存在，此外，在某些情况下，必须使用数值方法来计算多项式系数；
3. 所有考虑的获取多项式函数的方法都有一个共同的缺点——它们并不对应于最佳逼近多项式，即在函数逼近的整个区间内，与真实值的最大偏差并不相同。