LeetCode笔记 NO.704二分查找

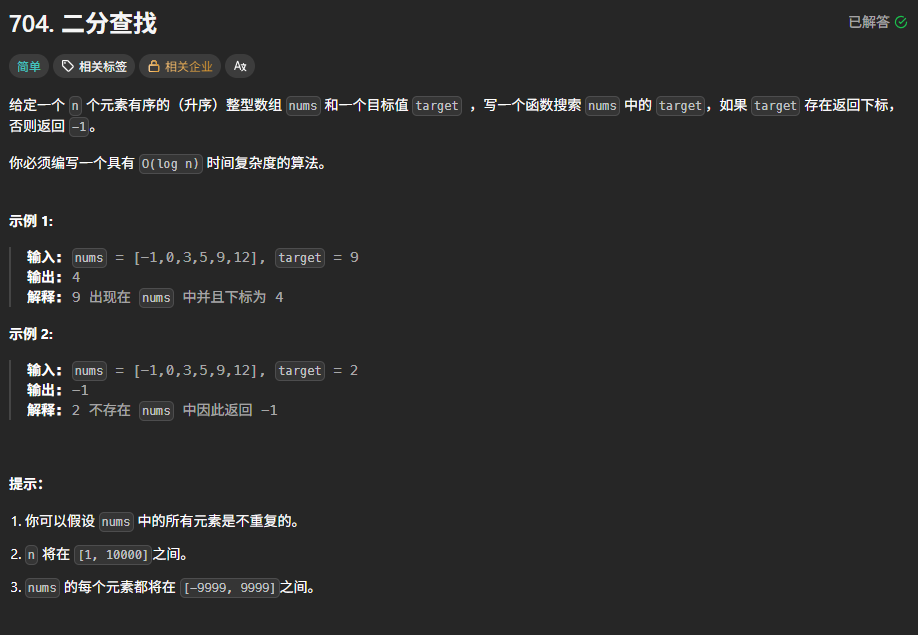
题目描述

 1.撸起袖子就是干！

 1.1代码

 public int mySearch(int[] nums, int target) {
        int j = nums.length-1;
        int i = 0;
        int result = -1;
        //边界条件有问题，当数组只有相同元素时条件错误
        while(target > nums[i] && target < nums[j] && i != j){
            int k = (i+j)/2;
            if(k == i || k == j){
                return result;
            }
            if(target > nums[k]){
                i = k;
            }else if(target < nums[k]){
                j = k;
            }else{
                result = k;
                break;
            }
        }
        return result;
    }

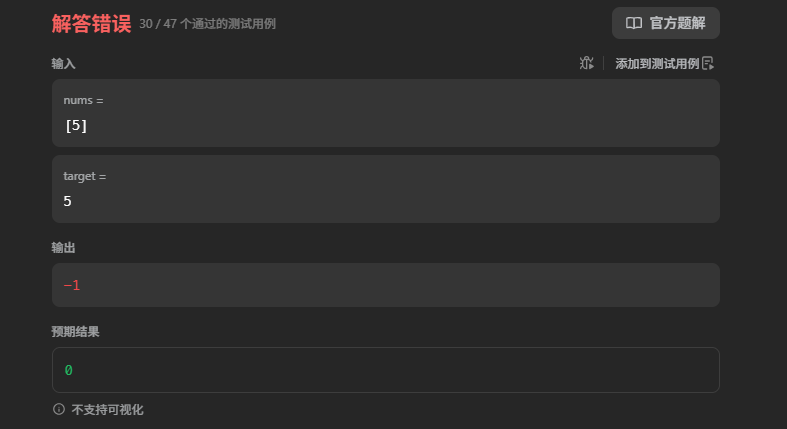
1.2报错

 2.题解

2.1方法一：二分查找

在升序数组 nums 中寻找目标值 target，对于特定下标 i，比较 nums[i] 和 target 的大小：

如果 nums[i]=target，则下标 i 即为要寻找的下标；

如果 nums[i]>target，则 target 只可能在下标 i 的左侧；

如果 nums[i]<target，则 target 只可能在下标 i 的右侧。

基于上述事实，可以在有序数组中使用二分查找寻找目标值。

二分查找的做法是，定义查找的范围 [left,right]，初始查找范围是整个数组。每次取查找范围的中点 mid，比较 nums[mid] 和 target 的大小，如果相等则 mid 即为要寻找的下标，如果不相等则根据 nums[mid] 和 target 的大小关系将查找范围缩小一半。

由于每次查找都会将查找范围缩小一半，因此二分查找的时间复杂度是 O(logn)，其中 n 是数组的长度。

二分查找的条件是查找范围不为空，即 left≤right。如果 target 在数组中，二分查找可以保证找到 target，返回 target 在数组中的下标。如果 target 不在数组中，则当 left>right 时结束查找，返回 −1。

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

3.二周目挑战BOSS

public int fixMySearch(int[] nums, int target) {
        int j = nums.length-1;
        int i = 0;
        int result = -1;
        //这里要是<= 如果是<存在当数组只有一个元素的情况
        while(i <= j){
            int k = (i+j)/2;
            if(target > nums[k]){
                //这里+1、-1是为了防止(i+j)/2 = i || j，使得代码无限循环
                i = k+1;
            }else if(target < nums[k]){
                j = k-1;
            }else{
                result = k;
                break;
            }
        }
        return result;
    }

AC了

4.程序员の沉淀

实际使用求中间mid索引建议用这种方法：int mid = left + (right-left)/2;

可以防止left+right溢出（超出整数范围）