leetcode刷题笔记-binary search

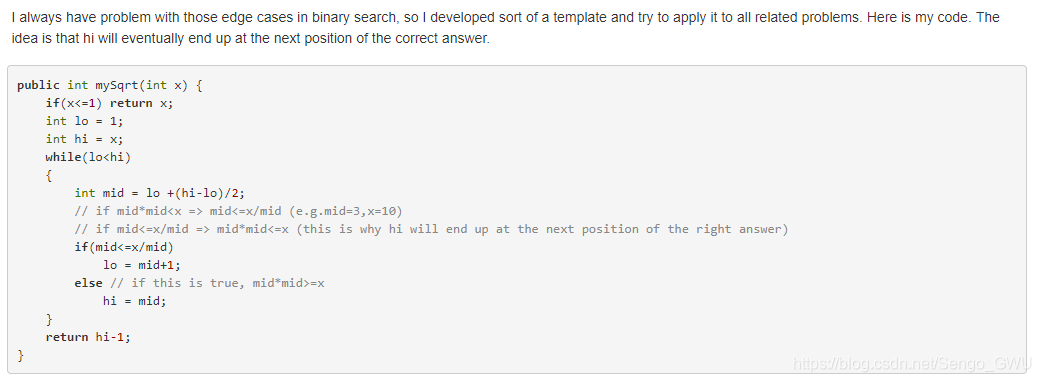
标准的bs:

def binary_search(arr, target):
    l, r = 0, len(arr) - 1
    while l < r:
        mid = l + (r - l) // 2
        if arr[mid] < target:
            l = mid + 1
        else:
            r = mid
    return r  # 返回的是右侧的
例子
【1,2,2,3】 target 2.1
返回的是3的位置

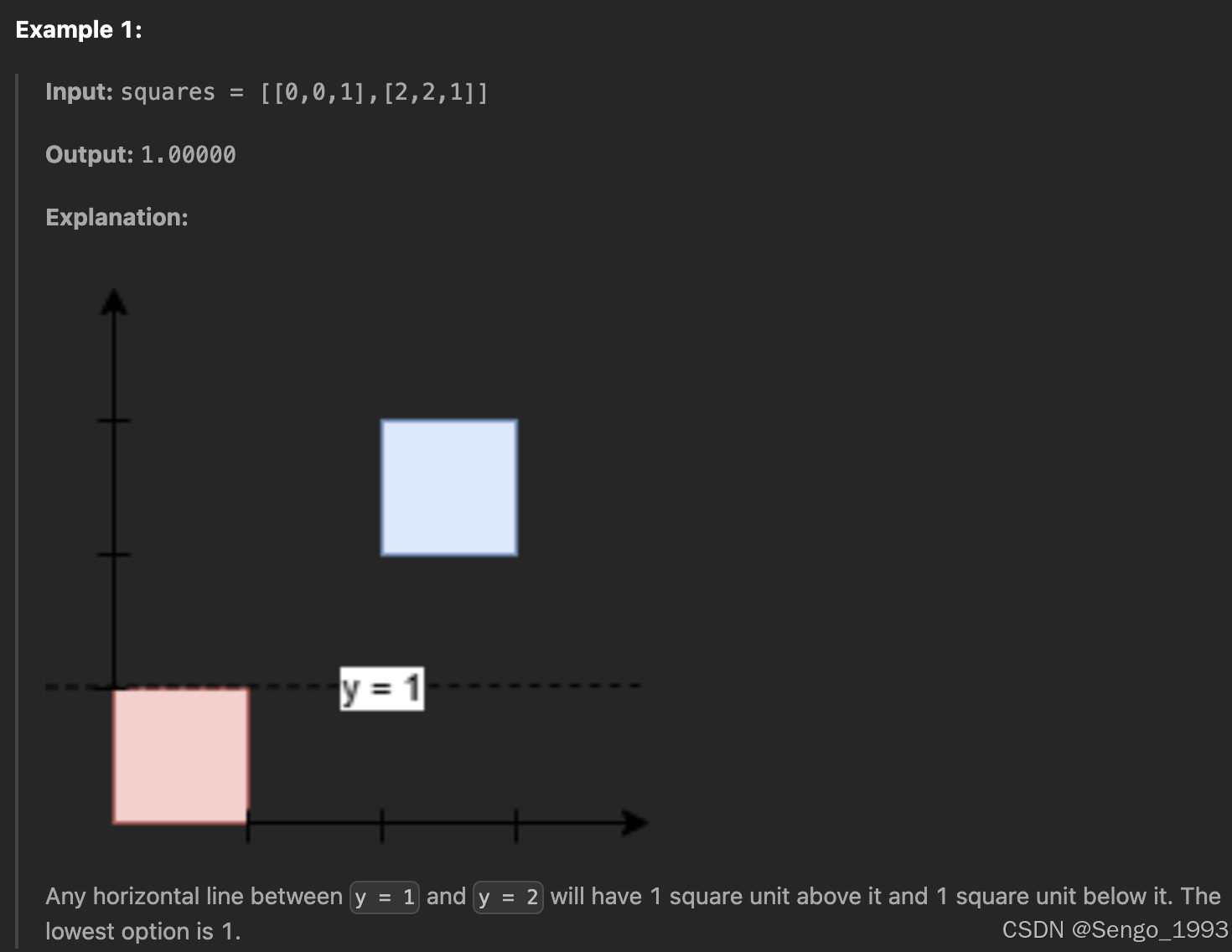
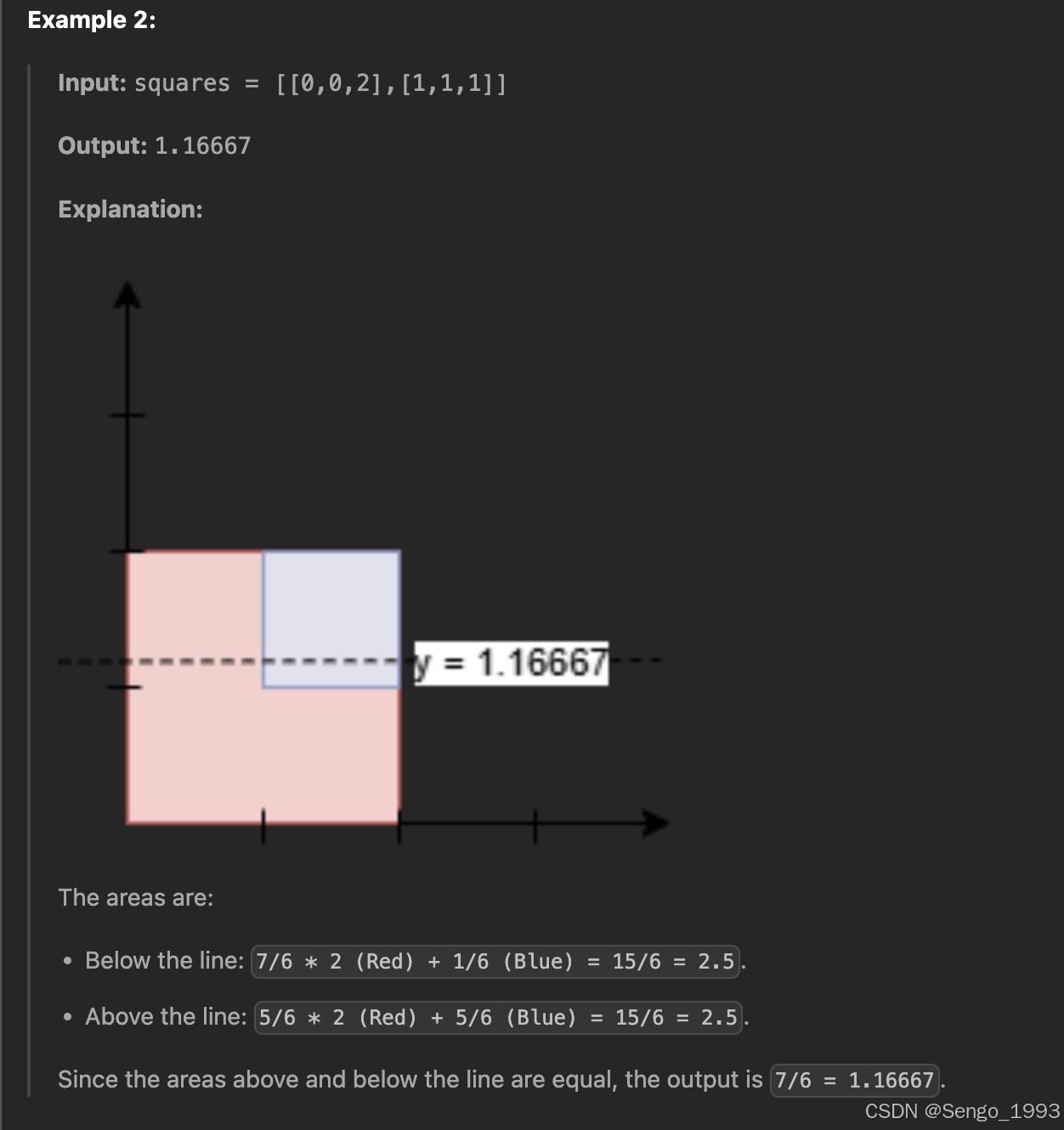
 3453. Separate Squares I

class Solution:
    def separateSquares(self, squares: List[List[int]]) -> float:
        # https://leetcode.com/problems/separate-squares-i/?envType=company&envId=google&favoriteSlug=google-thirty-days
        # Instead of checking the interval width directly, you can perform a fixed number of iterations say 60. Each iteration halves the search interval, guaranteeing that after a sufficient number of iterations, the interval is extremely narrow.
        # After each iteration, the width is halved. After 60 iterations, the width becomes: W/2^60
        def helper(line, squares):
            total = 0.0
            above = 0.0

            for x, y, l in squares:
                total += l*l

                if line <= y: # line is below square
                    above += l*l
                elif line < y + l: # line intersects theh square
                    above += ((y+l) - line) * l
            
            return above - (total - above) # above - below

        
        lo = 0
        hi = 2*1e9
        # loop all the squares to find the low and high
        for x, y, l in squares:
            lo = min(lo, float(y))
            hi = max(hi, float(y) + l)

        # binary search
        for _ in range(60):
            mid = (lo + hi) / 2.0 
            diff = helper(mid, squares)

            if diff > 0: # above > below
                # line should increase
                lo = mid
            else:
                hi = mid
        return hi

875. Koko Eating Bananas

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:

        def countDays(piles, k):
            h = 0
            for p in piles:
                h += math.ceil(p / k)
            return h
        l, r = 1, max(piles)
        while l < r:
            mid = (l + r) // 2
            countH = countDays(piles, mid)
            if countH <= h:
                r = mid
            else:
                l = mid + 1
        return l

1011. Capacity To Ship Packages Within D Days

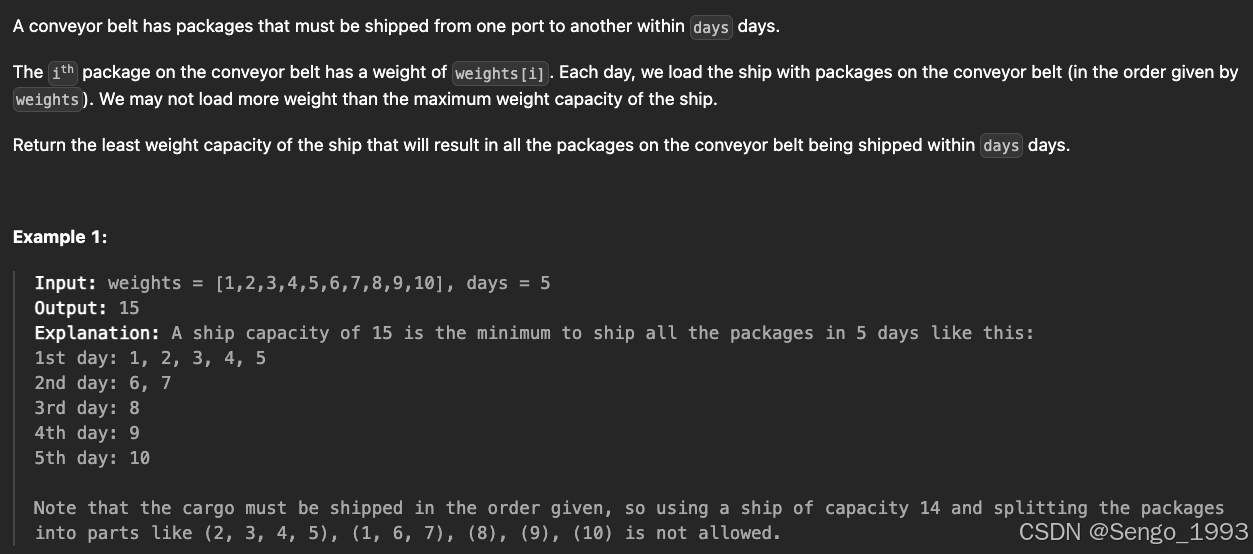
class Solution:
    def shipWithinDays(self, weights: List[int], days: int) -> int:
        # binary search 最小的capacity 从最大的重量开始，因为船至少得运得了它
        l, r = max(weights), sum(weights)

        while l < r:
            mid = (l+r) // 2
            curLoad = 0
            needDay = 0
            for w in weights:
                if curLoad + w > mid:
                    needDay += 1
                    curLoad = 0
                curLoad += w
            if curLoad > 0:
                needDay += 1
            if needDay > days:
                l = mid + 1
            else:
                r = mid
        return l

1885. Count Pairs in Two Arrays

class Solution:
    def countPairs(self, nums1: List[int], nums2: List[int]) -> int:
        '''
nums1[i] + nums1[j] > nums2[i] + nums2[j] is the same as (nums1[i] - nums2[i]) + (nums1[j] - nums2[j]) > 0

So, if we define NUM = [nums1[0]-nums2[0], nums1[1]-nums2[1], ...],
This problem can be rewritten as:
How many (i, j) pairs with i < j that NUM[i] + NUM[j] > 0
Given a value x, count the number of y in the nums that satisfies (y + x > 0)  -> Binary search
Time: n*log(n)
Space: O(n) if we copy the given nums, or O(1)
        '''

        nums = [x-y for x, y in zip(nums1, nums2)]
        re = 0
        nums.sort()

        def binary(target):
            l, r = 0, len(nums)
            while l < r:
                mid = (l+r) // 2
                if nums[mid] < target:
                    l = mid + 1
                else:
                    r = mid
            return l
        # print(nums)
        for i, x in enumerate(nums):
            target = 0 - x + 0.1
            idx = binary(target)