洛谷 ~ P1273 ~ 有线电视网（树形背包）

最新推荐文章于 2024-09-18 22:12:01 发布

原创最新推荐文章于 2024-09-18 22:12:01 发布 · 585 阅读

1 ·

CC 4.0 BY-SA版权

【树形DP】同时被 2 个专栏收录

12 篇文章

订阅专栏

【背包问题】

8 篇文章

订阅专栏

本文介绍了一种在树形结构上使用动态规划(DP)算法来解决最大利润转发问题的方法。通过定义状态dp[u][j]表示以u为根节点，转发到j个用户时的利润最大值，利用递归思想进行状态转移，最终求得转发利润最大化的用户数。文章详细阐述了算法流程，并提供了一个具体的实现代码示例。

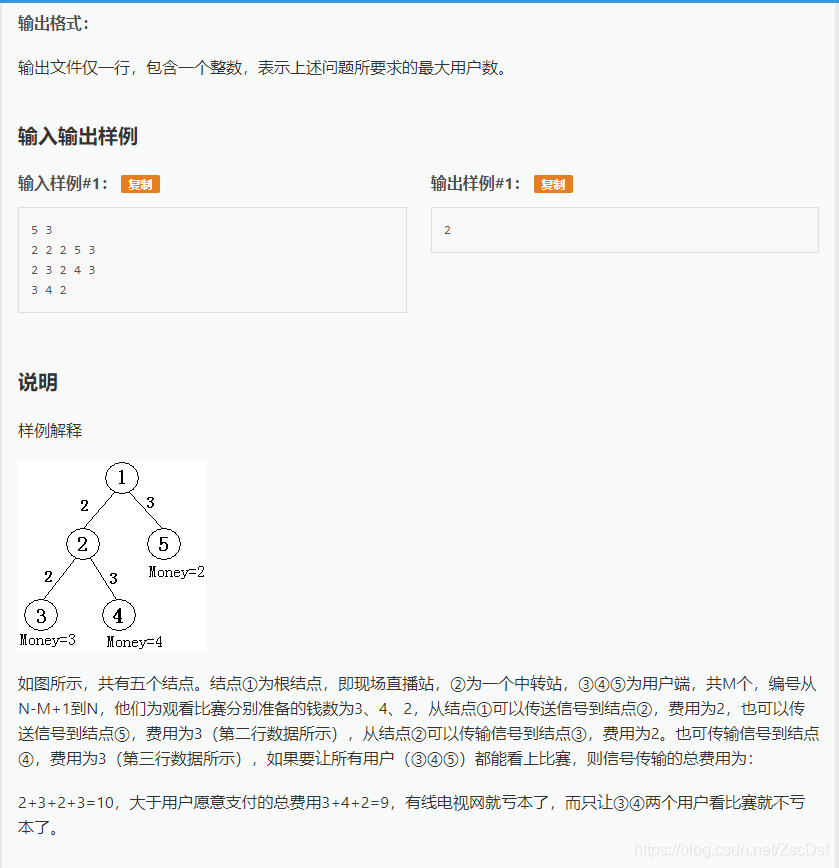
在这里插入图片描述

思路

$c [i]$ 表示该用户愿意支出的钱
$s z [u]$ 表示以u为根节点的子树有多少个用户。 $s z [u] + = s z [v]$
$d p [u] [j]$ 表示以 $u$ 为根节点，转发到 $u$ 个用户利润的最大值
如果 $u$ 为叶子结点即用户，则 $s z [u] = 1, d p [u] [1] = c [i]$ ，否则 $d p [u] [0] = 0$ 。
$d p [u] [j] = m a x (d p [u] [j], d p [u] [j - k] + d p [v] [k] + w (u, v)) ， (j : s z [u] - > 1), (k : 0 - > m i n (s z [v], j))$
$a n s = m a x (a n s, i) 当且仅当 d p [1] [i] > = 0$

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 3005;
const int INF = 0x3f3f3f3f;
int n, m, sz[MAXN], deg[MAXN], dp[MAXN][MAXN], c[MAXN];
vector<pair<int, int> > G[MAXN];
#define X first
#define Y second
void dfs(int u, int fa)
{
    dp[u][0] = 0;
    if (deg[u] == 1) sz[u] = 1, dp[u][1] = c[u];
    for (auto i : G[u])
    {
        int v = i.X, w = i.Y;
        if (v == fa) continue;
        dfs(v, u);
        sz[u] += sz[v];
        for (int j = sz[u]; j >= 1; j--)
            for (int k = 0; k <= min(sz[v], j); k++)
                dp[u][j] = max(dp[u][j], dp[u][j-k] + dp[v][k] - w);
    }
}
int main()
{
    memset(dp, -INF, sizeof(dp));
    scanf("%d%d", &n, &m);
    for (int u = 1; u <= n-m; u++)
    {
        int k, v, w; scanf("%d", &k);
        while (k--)
        {
            scanf("%d%d", &v, &w);
            G[u].emplace_back(v, w);
            G[v].emplace_back(u, w);
            deg[u]++, deg[v]++;
        }
    }
    for (int i = n-m+1; i <= n; i++) scanf("%d", &c[i]);
    dfs(1, -1);
    int ans = 0;
    for (int i = 0; i <= sz[1]; i++)
        if (dp[1][i] >= 0) ans = i;
    printf("%d\n", ans);
    return 0;
}
/*
5 3
2 2 2 5 3
2 3 2 4 3
3 4 2
*/