POJ ~ 1655 ~ Balancing Act （树的重心）

最新推荐文章于 2024-08-08 11:24:07 发布

原创最新推荐文章于 2024-08-08 11:24:07 发布 · 301 阅读

1 ·

CC 4.0 BY-SA版权

【树形DP】专栏收录该内容

12 篇文章

订阅专栏

本文深入探讨了树的重心概念及其算法实现，介绍了如何通过计算找到一棵树的重心，即那个使得所有子树中最大子树节点数最少的点。通过具体代码示例，详细解释了如何处理多组测试数据，求解树的重心并输出重心位置及最大子树的节点数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

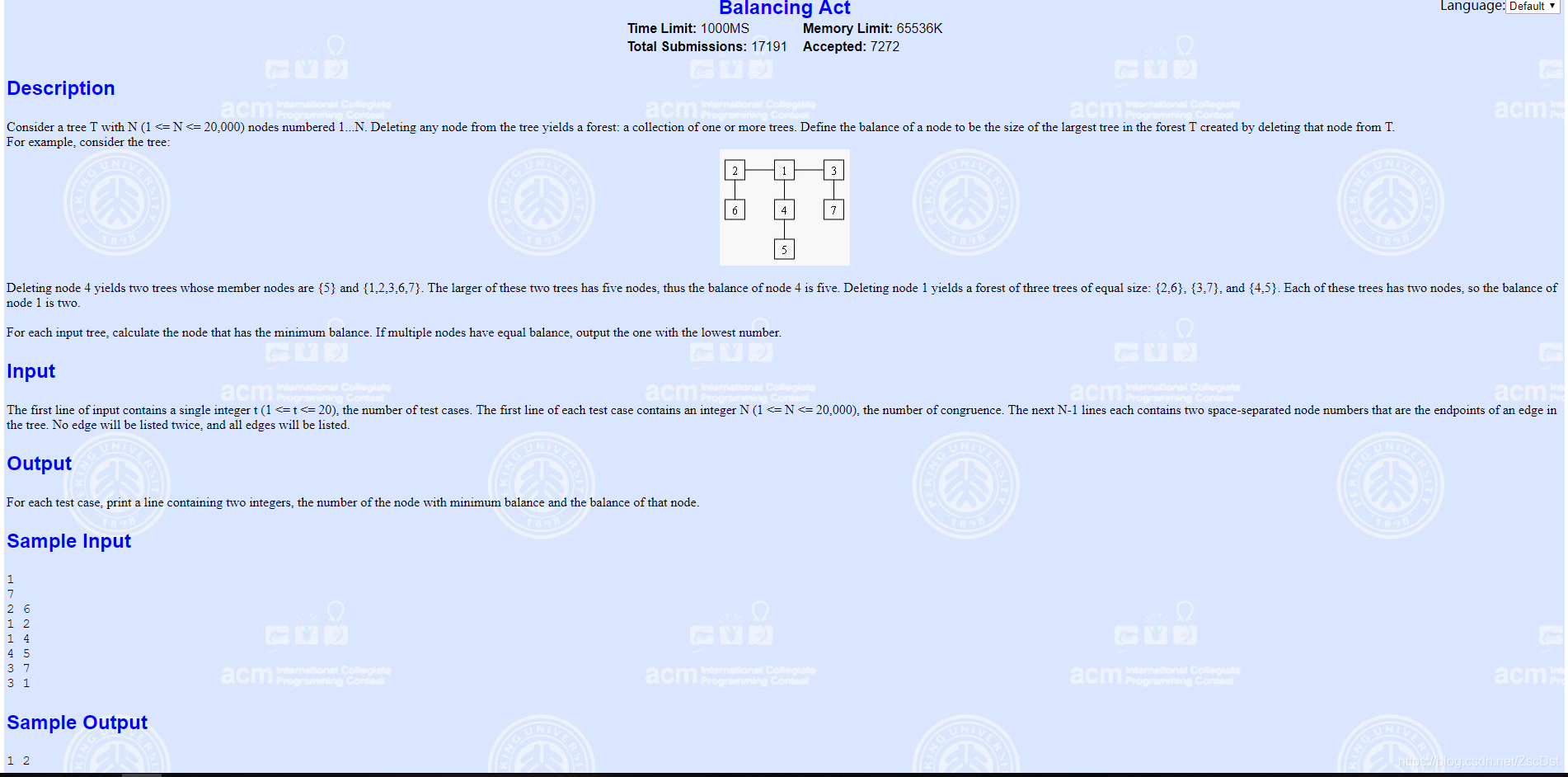
在这里插入图片描述

题意

树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。
T组测试数据，每组输入N，然后输入N-1条边，求树的重心。输出重心和最大的子树节点数。

思路

模板

//#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 1e5+5;
const int INF = 0x3f3f3f3f;
int n, sz[MAXN], pre[MAXN];
vector<int> G[MAXN];
int dfs(int u, int fa)
{
    sz[u] = 1;
    pre[u] = fa;
    for (int i = 0; i < G[u].size(); i++)
    {
        int v = G[u][i];
        if (v != fa)
            sz[u] += dfs(v, u);
    }

    return sz[u];
}
int main()
{
    int T; scanf("%d", &T);
    while (T--)
    {
        scanf("%d", &n);
        for (int i = 0; i <= n; i++) G[i].clear();
        for (int i = 1; i < n; i++)
        {
            int u, v; scanf("%d%d", &u, &v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dfs(1, -1);
        int ans = -1, MIN = INF;
        for (int u = 1; u <= n; u++)
        {
            int MAX = n - sz[u];
            for (int i = 0; i < G[u].size(); i++)
            {
                int v = G[u][i];
                if (v != pre[u])
                MAX = max(MAX, sz[v]);
            }
            if (MAX < MIN) MIN = MAX, ans = u;
        }
        printf("%d %d\n", ans, MIN);
    }
    return 0;
}
/*
1
7
2 6
1 2
1 4
4 5
3 7
3 1
*/