HDU ~ 5988 ~ Coding Contest （log乘变加 + 费用流）

最新推荐文章于 2019-09-23 19:03:35 发布

张松超

最新推荐文章于 2019-09-23 19:03:35 发布

阅读量341

点赞数

CC 4.0 BY-SA版权

分类专栏：【网络流/二分图匹配】

本文链接：https://blog.youkuaiyun.com/ZscDst/article/details/82969604

【网络流/二分图匹配】专栏收录该内容

37 篇文章

订阅专栏

本文介绍了一种利用费用流算法解决特定网络故障概率问题的方法。在ICPC比赛场景下，通过调整费用流算法以适应乘法运算，求解在网络中每个人都能吃到面包且网络不发生故障的最大概率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

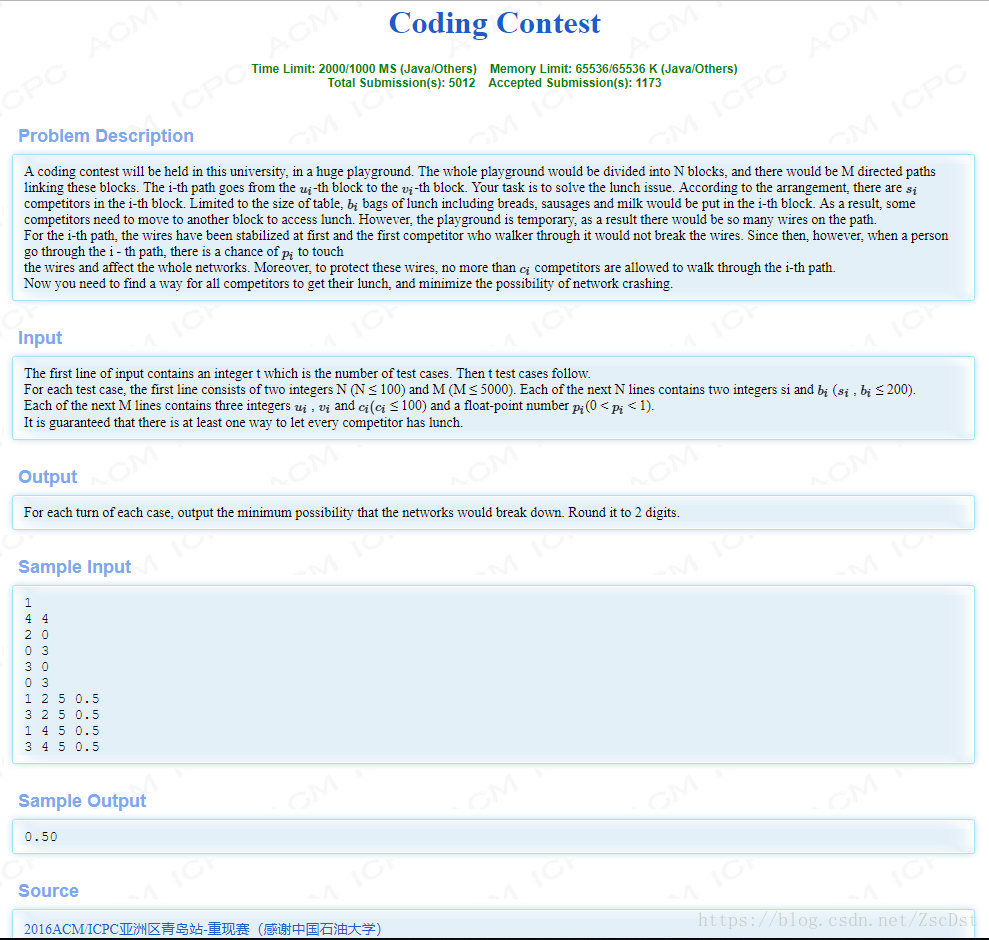
题意

在ICPC比赛现场，有N个点，M条路。每个点有s[i]个人和b[i]个面包，每条路上都有插线板，最多允许通过c[i]个人，每个人通过的时候有p[i]的概率会提到插线板，踢到插线板会使网络故障，但是每条路第一个人通过的时候一定不会踢到插线板。问使得每个人都能吃上面包且网络不发生故障的最大概率。保证有解。

思路

明显的费用流。最大不故障的概率 = 1 - 最小故障的概率，这样就可以求最小费用了。但是正常的费用流的费用是符合加法的，而本题的费用是乘起来的。我们应该吧乘法转化为加法，很容易就想到使用对数函数就OK了，最终答案我们在求回来即可。建图如下：

建立超级源点s，超级汇点 t

1. s 往人比面包多的点连边，容量为s[i]-b[i]，费用为0

2.面包比人多的点往 t 连边，容量为b[i]-s[i]，费用为0

3.原图中的边，容量为c[i]，费用为 $-ln(1.0-p[i])$

求得最小花费cost，答案为 $1-e^{-cost}$ 。

对了，记得SPFA的松弛步骤中需要加eps修正，否则会超时。

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 5;
const int INF = 0x3f3f3f3f;
const double eps = 1e-7;
struct Edge
{
    int from, to, cap, flow; double cost; //起点,终点,容量,流量,花费
    Edge(int u, int v, int c, int f, double w):from(u), to(v), cap(c), flow(f), cost(w) {}
};
struct MCMF
{
    int n, m;                //结点数,边数(包括反向弧),源点s,汇点t
    vector<Edge> edges;            //边表。edges[e]和edges[e^1]互为反向弧
    vector<int> G[MAXN];           //邻接表，G[i][j]表示结点i的第j条边在edges数组中的序号
    bool inq[MAXN];                //是否在队列中
    double d[MAXN];                   //Bellman-Ford
    int p[MAXN];                   //上一条弧
    int a[MAXN];                   //可改进量
 
    void init(int n)
    {
        this->n = n;
        edges.clear();
        for (int i = 0; i <= n; i++) G[i].clear();
    }
 
    void AddEdge(int from, int to, int cap, double cost)
    {
        edges.push_back(Edge(from, to, cap, 0, cost));
        edges.push_back(Edge(to, from, 0, 0, -cost));
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
 
    bool BellmanFord(int s, int t, int &flow, double& cost)//SPFA
    {
        for (int i = 0; i <= n; i++) d[i] = INF, inq[i] = false;
        d[s] = 0; inq[s] = true; p[s] = 0; a[s] = INF;
 
        queue<int> Q;
        Q.push(s);
        while (!Q.empty())
        {
            int u = Q.front(); Q.pop();
            inq[u] = 0;
            for (int i = 0; i < G[u].size(); i++)
            {
                Edge& e = edges[G[u][i]];
                if (e.cap > e.flow && d[e.to] > d[u] + e.cost + eps)
                {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if (!inq[e.to]) { Q.push(e.to); inq[e.to] = true; }
                }
            }
        }
        if (d[t] == INF) return false;
        flow += a[t];
        cost += d[t] * a[t];
        for (int u = t; u != s; u = edges[p[u]].from)
        {
            edges[p[u]].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return true;
    }
 
    int MinCostMaxFlow(int s, int t, double& cost)
    {
        int flow = 0; cost = 0;
        while (BellmanFord(s, t, flow, cost));
        return flow;
    }
 
}solve;
int main() 
{
    int T; scanf("%d", &T);
    while (T--)
    {
        int n, m; scanf("%d%d", &n, &m);
        int s = 0, t = n + 1;
        solve.init(t);
        for (int i = 1; i <= n; i++)
        {
            int a, b; scanf("%d%d", &a, &b);
            if (a > b) solve.AddEdge(s, i, a-b, 0);
            else solve.AddEdge(i, t, b-a, 0);
        }
        for (int i = 1; i <= m; i++)
        {
            int a, b, c; double d; scanf("%d%d%d%lf", &a, &b, &c, &d);
            d = -log(1-d);
            solve.AddEdge(a, b, 1, 0);
            if (c > 1) solve.AddEdge(a, b, c-1, d);
        }
        double cost;
        solve.MinCostMaxFlow(s, t, cost);
        double ans = 1-exp(-cost);
        printf("%.2f\n", ans);
    }
    return 0;
}
/*
1
4 4
2 0
0 3
3 0
0 3
1 2 5 0.5
3 2 5 0.5
1 4 5 0.5
3 4 5 0.5
*/