204. 计数质数/C++

最新推荐文章于 2025-02-07 11:45:51 发布

原创最新推荐文章于 2025-02-07 11:45:51 发布 · 208 阅读

0 ·

CC 4.0 BY-SA版权

LeetCode/C++ 专栏收录该内容

248 篇文章

订阅专栏

本文介绍了一种高效的寻找质数的方法——厄拉多塞筛法。通过迭代去除已知质数的倍数来筛选出指定范围内的所有质数。文章提供了详细的实现步骤和示例代码。

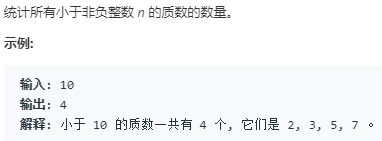
在这里插入图片描述
厄拉多塞筛法(Sieve of Eeatosthese)
选取2为质数，将2的倍数全部去掉；
选取3为质数，将3的倍数全部去掉；
4由于之前被去掉了，于是选择5为质数。。。

int countPrimes(int n) {
    if(n<=1) return 0;
    vector<bool> num(n,true);
    num[0]=false;
    
    for(int i=2;i<sqrt(n);++i){
        if(num[i]){
            int k = i;//此处由k=2优化得到
            //比如，5的2倍都被2的倍数去除了
            //5的3倍都被3的倍数去除了
            while(k*i<n){
                num[k*i]=false;
                ++k;
            }    
        }
    }
    int res = 0;
    for(int i=2;i<n;++i)
        if(num[i])
            ++res;
    return res;
}