本文介绍了在三次编程作业中，作者运用面向对象编程思想，通过递归下降法解析表达式，实现单变量多项式展开、带有指数函数和自定义函数的表达式处理，包括求导和优化策略。文章详细阐述了代码架构、递归解析过程和优化技巧，以及在整个过程中遇到的问题和解决方案。
前言
第一单元的主题是表达式展开，主要是学习面向对象编程的思想，通过类来管理对象。我们需要从数据维度和行为维度对类进行衡量和考虑。抽象层次的使用可以让我们的代码减少冗余，达到高内聚低耦合。数据抽象层次可以通过继承实现，行为抽象层次可以使用继承或接口实现。在文法分析中，递归下降法给我们提供了很大的帮助。运算过程中，递归层次同样也简化了问题的解决。本单元共有三次作业——单变量多项式展开，含有指数函数、嵌套括号、自定义函数的多项式展开，含有求导算子、支持定义时调用“已定义”函数的自定义函数。
不难发现，三次作业的要求逐次变高，复杂度也是稳步上升。就好像是初学做饭的我，刚学会了和面就让我蒸一锅馒头，刚学会了蒸馒头又让我包包子。新的要求总是在push，好在三周的时间第一单元终于结束。下面我将分别对三次作业进行分析总结。
第一次作业分析
第一次作业的任务是读入一个含加、减、乘、乘方以及括号（括号深度至多为1层）的单变量表达式，需要进行恒等变形和括号展开。
代码UML类图
本次作业代码UML类图如下所示
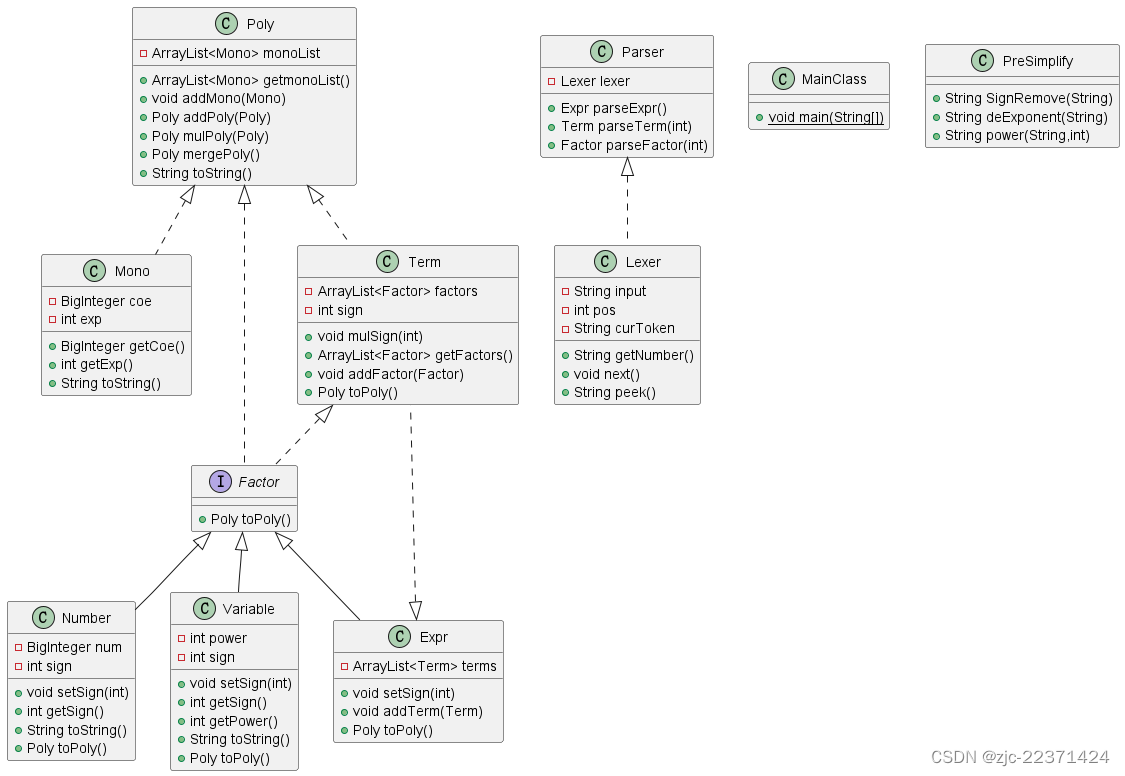
代码架构分析
首先可以将需要解析的表达式结构划分为表达式(Expr)、项(Term)、因子(Factor)三个层次。表达式由项相加而得，项又由因子相乘而得，因子有表达式因子、幂函数、常数因子。根据面向对象的思想，我们对这些类型分别建类。Expr中有容器来容纳Term，Term中有容器来容纳Factor。
理清层次之后，我们还需要解决两个问题。一是将表达式解析出来，即知道表达式是什么。二是对表达式进行展开计算。
递归下降法
这里主要对应我的代码中 Parser 和 Lexer 两个类。
Lexer类主要进行词法分析，通过 peek 方法为上层语法分析的 Parser 类提供当前位置信息，通过 next 方法移动到下一个语法单元。
Parser类沿用了oolens中递归下降法解析表达式的思想，这里通过 parseExpr 解析表达式，parseTerm 解析项，parseFactor 解析因子，每个层次的解析都遵循形式化的表述。因为第一项可能带正负号，所以我先解析了正负号，之后通过 while 语句块将所有的Term和Factor解析出来。
表达式展开
不难发现，表达式展开后的最终结果具有多项式形式的一般形式——
$$
Expr = \sum a_ix^{n_i}
$$
作为结果的多项式是一系列单项式求和的结果（这里我的单项式的正负体现在了系数中），所以自然而然我就建立了主要针对计算的Poly（多项式类）和Mono（单项式类）。
Mono类具有两个属性，coe（系数）和 exp（x的指数）。toString()方法在输出结果的时候可以将单项式输出为 "coe*x^exp"的形式。
Poly类具有一个Arraylist容器的属性，用来记录其包含的Mono单项式，此外有 addPoly() , mulPoly() , mergePoly() 等方法进行多项式加乘以及合并同类项的运算。toString() 方法可以将Poly中的Mono的字符串连接起来，形成多项式的字符串。
之后我们就可以在Expr、Term、Factor三个层次中分别写一个topoly方法，这里我将具有topoly方法的Factor设置为接口，其中包含因子中的表达式、常量和幂函数因子。从底层到高层，这里也使用了递归的思想。
Number和 Variable的topoly()都是转化成只有一个 mono 的 poly ，如 常量因子 3 可以转化为 3*x^0 ，变量因子 x^2 可以转化为 1 *x^2 。
Term 的topoly()就是将Factor类的对象topoly之后用mulpoly()乘起来。
Expr的topoly()就是将Term类的对象topoly之后用addpoly()求和之后进行mergepoly()的同类项合并。
其他
1.表达式预处理：我创建了一个 PreSimplify 类，预处理过程中，我显示将输入中的空白符删除，之后将连续的+-号合并成一个。
2.优化思路：
对于优化主要体现在了Mono类中 toString 方法：
如果单项式系数为0，则输出0。
如果单项式系数为1，则可以省略系数，只输出幂函数
$$
x^n
$$
如果单项式系数为-1，则可以省略系数，输出幂函数
$$
-x^n
$$
如果单项式指数为0，则可以省略幂函数，只输出系数。
如果单项式指数为1，则可以省略指数部分的^exp，只输出a*x。
代码复杂度分析
image-20240319144434577
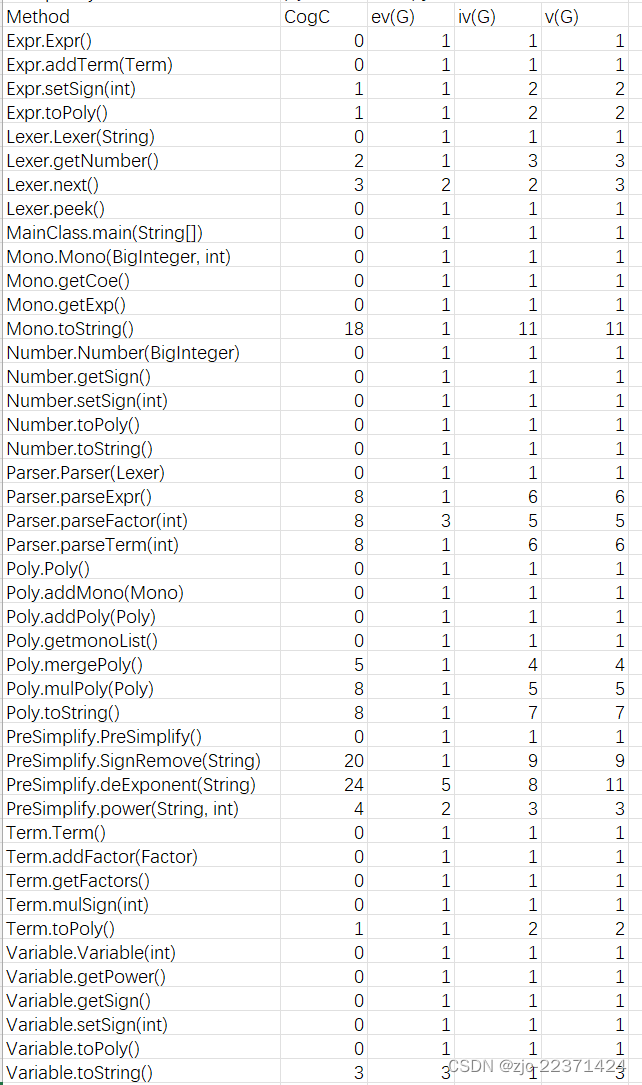
可以看出，Mono类中的tostring()方法在生成单项式字符串时需要针对系数、指数具体情况进行讨论，使用了较多的if-else分支，复杂度较高在所难免。
PreSimplify中的SignRemove()方法需要去除连续正负号，对字符串的解析过程尚有简化空间。对于deExponent()方法，在第一次作业中，我主要使用了“原字符串”+“*”+...去掉指数，这样使代码耦合度很高，第二次作业中我将采用解析过程中使用多项式乘法去指数，降低代码复杂度。
第二次作业分析
第二次作业在第一次作业的基础上新增了支持嵌套多层括号，指数函数因子，自定义函数因子。
代码UML类图
代码架构分析
第一次作业到第二次作业的跨度比较大，但递归下降法仍能够给我们提供很大帮助，甚至新增的括号嵌套功能无需新增迭代内容即可解决。下面我们亟需解决一下几个难题：
指数函数如何解析？
如何解析自定义函数？如何将自定义函数的实参带入到函数定义式中？
这次作业中我们不能延续使用 a*x^n 作为Mono的一般形式，那我们应用什么代替？
指数函数的解析
根据题目信息，指数函数由因子、指数构成，所以我新创建了一个ExpoFactor类，其factor属性记录其因子，power属性记录其次数。
为了解析指数函数，我在 Parser 类中新增了 parseExpoFactor() 方法，此方法在 parseFactor() 中被调用。当我们在parseFactor() 中lexer.peek()发现为“e”时，就调用parseExpoFactor() 方法，先对exp()中的因子进行解析，之后在解析指数函数的指数，最后将结果保存到一个新的 ExpoFactor 对象中返回。
自定义函数的定义和解析
首先，我新建了 FuncFactor 类，属性有 newfunc 和 expr，为自定义函数对象。
//FuncFactor.java private String newFunc; //将函数实参带入形参位置后的结果 private Expr expr; //将newFunc解析成表达式后的结果
对于自定义函数的处理我没有直接使用字符串替换，借鉴了hyggge学长的思路，我创立了一个工具类Definer，来处理自定义函数。这里我也学习到了设置静态属性和方法的思想，这样意味着我们可以无需实例化对象，直接通过类名即可调用。
funcMap可以通过函数名来获得函数定义式，paraMap可以通过函数名来获得形参列表(x/y/z)。
//Definer.java private static HashMap<String, String> funcMap = new HashMap<>(); //通过函数名f/g/h获得函数定义式 private static HashMap<String, ArrayList<String>> paraMap = new HashMap<>(); //通过函数名来获得函数的形参列表
该类的两个方法：
//Definer.java
public static void addFunc(String input){};
public static String callFunc(String name, ArrayList<Factor> actualParas);
前者在函数定义时使用，将输入的函数表达式进行解析，记录函数定义式和形参列表。
后者在函数调用时使用，传入参量为函数名和实参列表，之后可以根据形参列表和实参列表建立一一对应的关系。之后遍历函数定义式字符串，将形参替换成实参即可。
之后我们就可以进行自定义函数的解析了，先解析函数名，之后解析实参（因子）。
private FuncFactor parseFuncFactor(String name, int sign) {
ArrayList<Factor> actualParas = new ArrayList<>();
//...
while (lexer.peek().equals(",")) {
lexer.next();
if (lexer.peek().equals("-")) {
lexer.next();
actualParas.add(parseFactor(-sign));
} else if (lexer.peek().equals("+")) {
lexer.next();
actualParas.add(parseFactor(sign));
} else {
actualParas.add(parseFactor(sign));
}
}
//...
return new FuncFactor(name, actualParas);
}
这是我们只是完成了一半工作，下面还需要对函数表达式进行解析。解析过程也是在FuncFactor中实现。
public FuncFactor(String name, ArrayList<Factor> actualParas) {
StringBuilder newStr = new StringBuilder().append("(");
newStr.append(Definer.callFunc(name, actualParas)).append(")");
this.newFunc = newStr.toString();
this.expr = this.setExpr();
}
private Expr setExpr() {
String str = newFunc.replaceAll("\\s*", "");
PreSimplify preSimplify = new PreSimplify();
String str1 = preSimplify.SignRemove(str);
Lexer lexer = new Lexer(str1);
Parser parser = new Parser(lexer);
return parser.parseExpr();
}
callFunc实现了将实参带入，得到了新的字符串 newFunc，之后调用了此类中的方法setExpr将字符串解析成了 Expr 返回。
这样，自定义函数的解析也就结束了。
表达式展开
由于这次新增了指数函数，所以原来的mono的单项式一般形式不能继续沿用，但是原来的代码架构和运算方法可以延续。多项式最小单元一般形式为
$$
ax^n*exp(Factor)
$$
//Mono.java private BigInteger coe; //系数 private BigInteger exp; //次数 private Poly eback; //指数函数底数 private BigInteger epow; //指数函数次数
指数函数的底数本身是一个表达式因子，但是我们可以在解析过程中通过topoly()方法将其转换为多项式。因为Mono类的属性发生了改变，所以addPoly()，mulPoly() , powPoly() ，mergePoly()这些方法也需改变，这里不再一一赘述。只重点讲一下mergePoly()合并同类项时如何判断两个Mono是否可以合并。
两个Mono对象合并的条件是 x 的指数要相等并且指数函数的底数 eback 相等，x的指数相等很好判断，关键是判断eback的相等，这就需要判断多项式相等。 敏锐的同学可以发现这已经陷入了循环的地步。但不用担心，我们可以通过递归解决这个问题。最后一定可以通过没有exp()项的单项式比较找到出口。多项式判等如下：
//Poly.java
public static boolean equals(Poly a, Poly b) {
int asize = 0;
int bsize = 0;
for (Unit unit : a.unitList) {
if (!unit.getCoe().equals(BigInteger.ZERO)) {
asize++;
}
} //将指数乘到exp()中
for (Unit unit : b.unitList) {
if (!unit.getCoe().equals(BigInteger.ZERO)) {
bsize++;
}
}
if (asize != bsize) {
return false;
}
for (Unit unit1 : a.unitList) {
int flag = 0;
for (Unit unit2 : b.unitList) {
if (Unit.mergeAble(unit1, unit2)) {
if (!unit1.getCoe().equals(unit2.getCoe())) {
return false;
}
flag = 1;
break;
}
}
if (flag == 0) {
return false;
}
}
return true;
}
代码复杂度分析
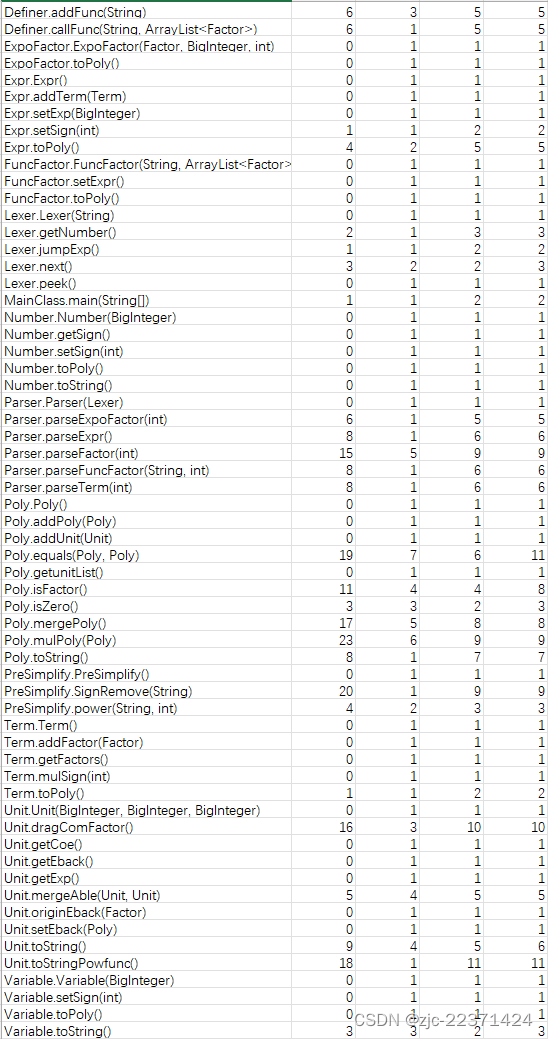
从图中可以看出，复杂方法主要集中在Poly和Mono（即图中的Unit类），主要是新增的指数函数部分导致add和mul运算进行的操作变得复杂，输出时tostring()的过程中也需要更多的判断分支。
第三次作业分析
第三次作业新增了求导算子，函数表达式中支持调用其他“已定义的函数”。第二点在我之前作业的架构中就已经可以实现。所以主要问题就是解决求导算子。
代码UML类图
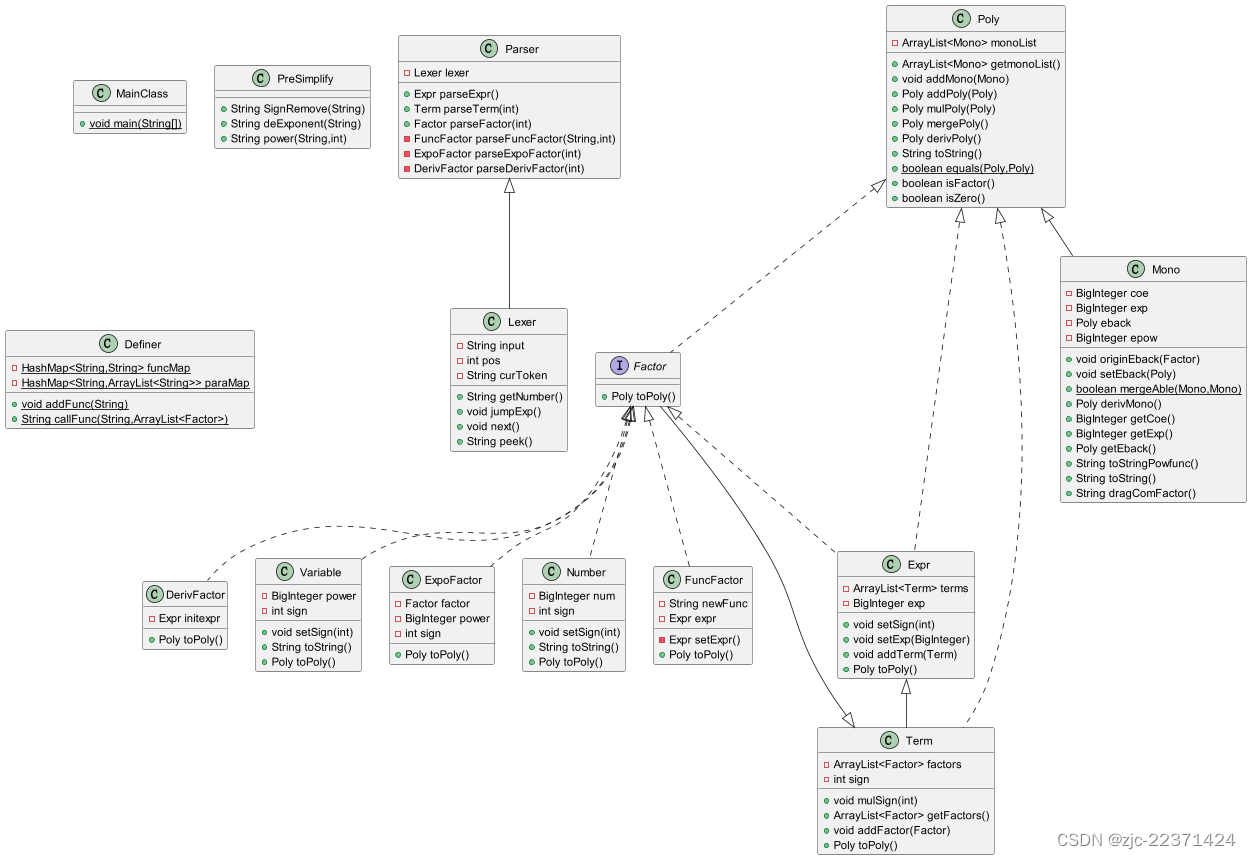
代码架构分析
新建了一个DerivFactor类用来表示求导算子，其中只有一个Expr属性来记录被求导的表达式。
//DerivFactor.java private Expr initexpr; //初始dx() 括号内的expr
对表达式求导，也就是对表达式使用topoly()方法后的poly多项式求导。多项式求导是单项式Mono求导之和，所以只需要对Mono求导即可。单项式求导需要讨论单项式x的指数和exp()的底数，即一个为0，两个为0，或者都不为0的情况。之后根据乘法求导法则就可以解决问题。
//Mono.java
public Poly derivMono() { //单项式求导 应该返回多项式
Poly poly = new Poly();
int sum = 0;
for (Mono mono : eback.getmonoList()) {
if (!mono.coe.equals(BigInteger.ZERO)) {
sum++;
}
}
boolean flagExp = (exp.compareTo(BigInteger.ZERO) > 0); //判断x的指数是否为0
boolean flagEback = (sum > 0); //判断e指数是否为0
if (!flagEback && !flagExp) {
Mono mono = new Mono(BigInteger.ZERO, BigInteger.ZERO, BigInteger.ZERO);
mono.originEback(new Number(BigInteger.ZERO));
poly.addMono(mono);
return poly;
} else if (!flagEback) {
Mono mono = new Mono(coe.multiply(exp), exp.subtract(BigInteger.ONE), BigInteger.ZERO);
mono.originEback(new Number(BigInteger.ZERO));
poly.addMono(mono);
return poly;
} else if (!flagExp) {
Mono mono = new Mono(coe, BigInteger.ZERO, BigInteger.ONE);
mono.eback = this.eback;
poly.addMono(mono);
return poly.mulPoly(eback.derivPoly());
} else {
Mono mono1 = new Mono(coe.multiply(exp), exp.subtract(BigInteger.ONE), BigInteger.ONE);
mono1.eback = this.eback;
poly.addMono(mono1);
Poly poly2 = new Poly();
poly2.addMono(this);
return poly.addPoly(poly2.mulPoly(eback.derivPoly()));
}
}
除此之外，我还对结果的长度进行了优化，在exp()底数eback这个多项式中，对每个单项式的系数求最大公因数，将公因数提出的字符串长度与不提出保持原样进行比较，在toString()时使用长度较短的。求公因数的方法为BigInterger类自带方法。
代码复杂度分析
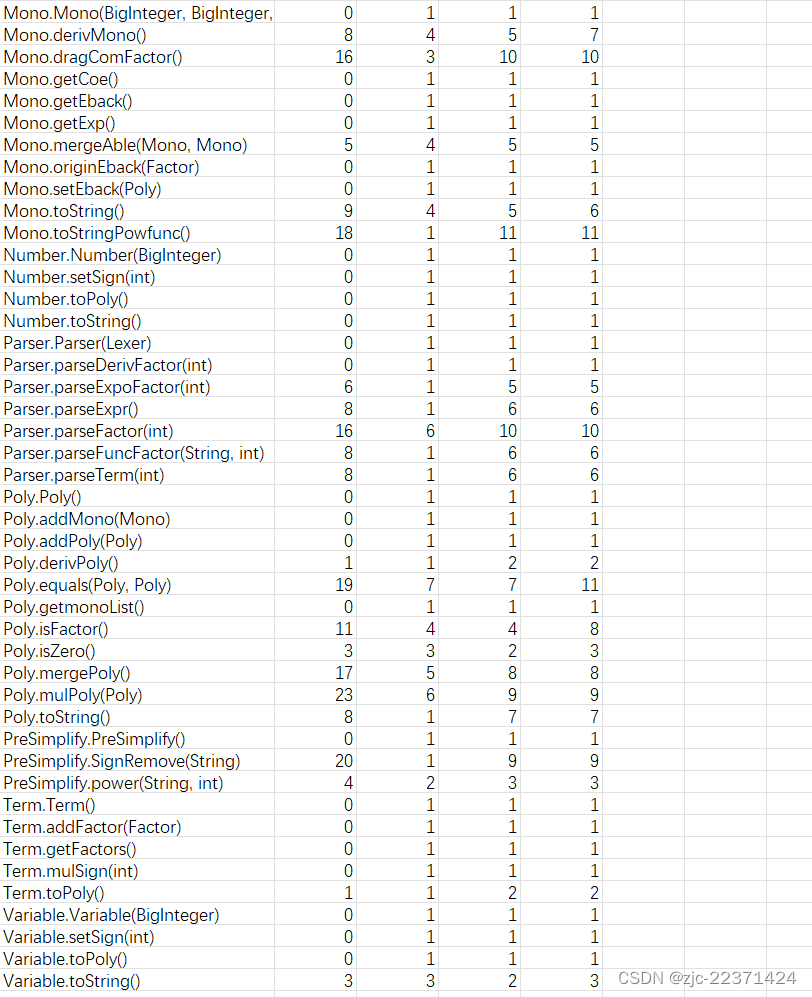
这次作业过后复杂度基本与第二次作业完成时保持一致，比较满意。
Bug分析
比较幸运的是，第一单元的三次作业中强测均未出现bug，也没有被同学们hack成功，主要是得益于同学们写的评测机，平均每次作业都可以帮我测试出2~3个bug。那我就谈谈对作业完成过程中的debug吧，debug首先需要准确定位，我们要不断简化评测机发现的错误的数据，之后通过调试就可以定位到bug所在的位置。由于前面作业中我的实参是通过逗号作为间隔进行解析的，第三次作业新增了实参可以包含函数因子，所以这里出现了错误。接下来还是需要在迭代的过程中将问题考虑全面，不能想当然认为之前的方法无懈可击。
架构设计体验
在这三次作业中我并没有重构，主要得益于递归下降算法的天然优势和合理的需求预测。
首先，我并没有采用正则表达式来解析表达式，而是果断选择了递归下降算法。这个算法在三次作业中都是适用的，我相信即使再增加因子类型，递归下降同样也可以解决，嵌套括号更是可以由递归的思想解决。
其次，我在做每一次作业时，并不仅仅着眼于本次作业的要求，还对下次作业的要求进行一定预测，然后在coding的时候尽量关注代码的可扩展性，为下一次作业的迭代做好准备。
心得体会
关注讨论区：当架构没有思路时，我们可以看看讨论区借鉴学长和同学们的思路。
优化时保证正确性：正确性永远是第一位的。
注重代码可拓展性：要通过合理的架构设计，灵活运用继承、接口、多态等使自己的代码可拓展性高。
扫一扫
2008
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
