本文聚焦神经网络反向传播，介绍了神经网络结构，推导损失函数J(w)对w和b的梯度，指出求权重矩阵w梯度需用到后面矩阵的梯度∂hL∂J。还探讨了通过非线性变换fL求∂hL∂J，分析了Sigmoid、tanh、ReLU三种常见函数下的计算方法。
神经网络结构：
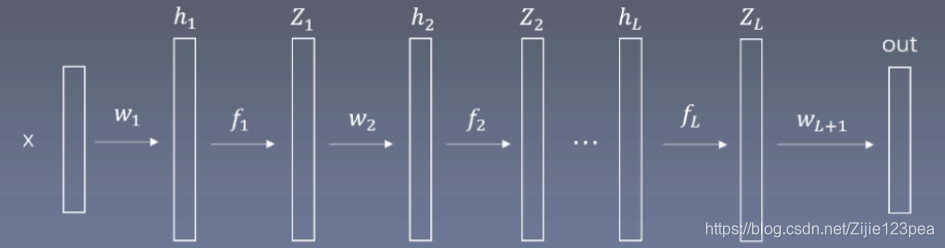
OUT=ZLwL+1+b~L+1OUT=Z_Lw_{L+1}+\tilde b_{L+1}OUT=ZLwL+1+b~L+1
设：
ZL=[z11z12z13z21z22z23]Z_L=\left[\begin{matrix}z_{11}&z_{12}&z_{13}\\z_{21}&z_{22}&z_{23}\end{matrix}\right]ZL=[z11z21z12z22z13z23],WL+1=[w11w12w21w22w31w32]W_{L+1}=\left[\begin{matrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{matrix}\right]WL+1=⎣⎡w11w21w31w12w22w32⎦⎤,
bL+1=[b1b2]b_{L+1}=\left[\begin{matrix}b_1\\b_2\end{matrix}\right]bL+1=[b1b2]
b~L+1=[b11b12b21b22]\tilde b_{L+1}=\left[\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{matrix}\right]b~L+1=[b11b21b12b22],OUT=[o11o12o21o22]OUT=\left[\begin{matrix}o_{11}&o_{12}\\o_{21}&o_{22}\end{matrix}\right]OUT=[o11o21o12o22]
则：
ZLwL+1=[z11z12z13z21z22z23][w11w12w21w22w31w32]=[z11w11+z12w21+z13w31z11w12+z12w22+z13w32z21w11+z22w21+z23w31z21w12+z22w22+z23w32]Z_Lw_{L+1}=\left[\begin{matrix}z_{11}&z_{12}&z_{13}\\z_{21}&z_{22}&z_{23}\end{matrix}\right]\left[\begin{matrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{matrix}\right]=\left[\begin{matrix}z_{11}w_{11}+z_{12}w_{21}+z_{13}w_{31}&z_{11}w_{12}+z_{12}w_{22}+z_{13}w_{32}\\z_{21}w_{11}+z_{22}w_{21}+z_{23}w_{31}&z_{21}w_{12}+z_{22}w_{22}+z_{23}w_{32}\end{matrix}\right]ZLwL+1=[z11z21z12z22z13z23]⎣⎡w11w21w31w12w22w32⎦⎤=[z11w11+z12w21+z13w31z21w11+z22w21+z23w31z11w12+z12w22+z13w32z21w12+z22w22+z23w32]
OUT=[o11o12o21o22]OUT=\left[\begin{matrix}o_{11}&o_{12}\\o_{21}&o_{22}\end{matrix}\right]OUT=[o11o21o12o22]
o11=z11w11+z12w21+z13w31+b1o_{11}=z_{11}w_{11}+z_{12}w_{21}+z_{13}w_{31}+b_1o11=z11w11+z12w21+z13w31+b1
o12=z11w12+z12w22+z13w32+b2o_{12}=z_{11}w_{12}+z_{12}w_{22}+z_{13}w_{32}+b_2o12=z11w12+z12w22+z13w32+b2
o21=z21w11+z22w21+z23w31+b1o_{21}=z_{21}w_{11}+z_{22}w_{21}+z_{23}w_{31}+b_1o21=z21w11+z22w21+z23w31+b1
o22=z21w12+z22w22+z23w32+b2o_{22}=z_{21}w_{12}+z_{22}w_{22}+z_{23}w_{32}+b_2o22=z21w12+z22w22+z23w32+b2
反向传播的目的是优化各个www矩阵，fff不需要优化，因为里面没有参数。所以损失函数表示为J(w)J(w)J(w)。
下面算损失函数J(w)J(w)J(w)对www的梯度：
损失函数JJJ为预测值OUT减去实际标签值后，求MSE或CE，所以JJJ为列向量的范数或CE，与ooo和www有关系，所以用链式求导：
可以设∣∣ZLwL+1+b~L+1−Y∣∣2=J||Z_Lw_{L+1}+\tilde b_{L+1}-Y||^2=J∣∣ZLwL+1+b~L+1−Y∣∣2=J（此处范数为Frobenius范数，即矩阵元素绝对值的平方和再开平方；当然也可以选用CE或其他形式），aaa中包含www，则J(w)J(w)J(w)对www求梯度，即对www矩阵中每一个元素求梯度：
∂J∂w11=∂J∂o11z11+∂J∂o21z21\frac{\partial J}{\partial w_{11}}=\frac{\partial J}{\partial o_{11}}z_{11}+\frac{\partial J}{\partial o_{21}}z_{21}∂w11∂J=∂o11∂Jz11+∂o21∂Jz21，∂J∂w12=∂J∂o12z11+∂J∂o22z21\frac{\partial J}{\partial w_{12}}=\frac{\partial J}{\partial o_{12}}z_{11}+\frac{\partial J}{\partial o_{22}}z_{21}∂w12∂J=∂o12∂Jz11+∂o22∂Jz21
∂J∂w21=∂J∂o11z12+∂J∂o21z22\frac{\partial J}{\partial w_{21}}=\frac{\partial J}{\partial o_{11}}z_{12}+\frac{\partial J}{\partial o_{21}}z_{22}∂w21∂J=∂o11∂Jz12+∂o21∂Jz22，∂J∂w22=∂J∂o12z12+∂J∂o22z22\frac{\partial J}{\partial w_{22}}=\frac{\partial J}{\partial o_{12}}z_{12}+\frac{\partial J}{\partial o_{22}}z_{22}∂w22∂J=∂o12∂Jz12+∂o22∂Jz22
∂J∂w31=∂J∂o11z13+∂J∂o21z23\frac{\partial J}{\partial w_{31}}=\frac{\partial J}{\partial o_{11}}z_{13}+\frac{\partial J}{\partial o_{21}}z_{23}∂w31∂J=∂o11∂Jz13+∂o21∂Jz23，∂J∂w32=∂J∂o12z13+∂J∂o22z23\frac{\partial J}{\partial w_{32}}=\frac{\partial J}{\partial o_{12}}z_{13}+\frac{\partial J}{\partial o_{22}}z_{23}∂w32∂J=∂o12∂Jz13+∂o22∂Jz23
注意：此处因为WL+1=[w11w12w21w22w31w32]3×2W_{L+1}=\left[\begin{matrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{matrix}\right]_{3\times 2}WL+1=⎣⎡w11w21w31w12w22w32⎦⎤3×2，有两套参数，所以求损失函数时用Frobenius范数，即矩阵元素绝对值的平方和再开平方。
所以：
∂J∂WL+1=[∂J∂w11∂J∂w12∂J∂w21∂J∂w22∂J∂w31∂J∂w32]=[z11z21z12z22z13z23][∂J∂o11∂J∂o12∂J∂o21∂J∂o22]=ZLT∂J∂OUT\frac{\partial J}{\partial W_{L+1}}=\left[\begin{matrix}\frac{\partial J}{\partial w_{11}}&\frac{\partial J}{\partial w_{12}}\\\frac{\partial J}{\partial w_{21}}&\frac{\partial J}{\partial w_{22}}\\\frac{\partial J}{\partial w_{31}}&\frac{\partial J}{\partial w_{32}}\end{matrix}\right]=\left[\begin{matrix}z_{11}&z_{21}\\z_{12}&z_{22}\\z_{13}&z_{23}\end{matrix}\right]\left[\begin{matrix}\frac{\partial J}{\partial o_{11}}&\frac{\partial J}{\partial o_{12}}\\\frac{\partial J}{\partial o_{21}}&\frac{\partial J}{\partial o_{22}}\\\end{matrix}\right]=Z_L^T\frac {\partial J}{\partial OUT}∂WL+1∂J=⎣⎡∂w11∂J∂w21∂J∂w31∂J∂w12∂J∂w22∂J∂w32∂J⎦⎤=⎣⎡z11z12z13z21z22z23⎦⎤[∂o11∂J∂o21∂J∂o12∂J∂o22∂J]=ZLT∂OUT∂J
可见在线性变换的最后一层求导已经用到OUT的偏导数了。
损失函数J(w)J(w)J(w)对bbb的梯度：
bL+1=[b1b2]b_{L+1}=\left[\begin{matrix}b_1\\b_2\end{matrix}\right]bL+1=[b1b2]，拓展为：b~L+1=[b11b12b21b22]\tilde b_{L+1}=\left[\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{matrix}\right]b~L+1=[b11b21b12b22]
其实b11=b12=b1b_{11}=b_{12}=b_1b11=b12=b1,b12=b22=b2b_{12}=b_{22}=b_2b12=b22=b2
∂J∂b1=∂J∂o11+∂J∂o21\frac{\partial J}{\partial b_1}=\frac{\partial J}{\partial o_{11}}+\frac{\partial J}{\partial o_{21}}∂b1∂J=∂o11∂J+∂o21∂J
∂J∂b2=∂J∂o12+∂J∂o22\frac{\partial J}{\partial b_2}=\frac{\partial J}{\partial o_{12}}+\frac{\partial J}{\partial o_{22}}∂b2∂J=∂o12∂J+∂o22∂J
即：[∂J∂bL+1]=[∂J∂b1∂J∂b2]=[∂J∂o11+∂J∂o21∂J∂o12+∂J∂o22]\left[\begin{matrix}\frac{\partial J}{\partial b_{L+1}}\end{matrix}\right]=\left[\begin{matrix}\frac{\partial J}{\partial b_1}\\\frac{\partial J}{\partial b_2}\end{matrix}\right]=\left[\begin{matrix}\frac{\partial J}{\partial o_{11}}+\frac{\partial J}{\partial o_{21}}\\\frac{\partial J}{\partial o_{12}}+\frac{\partial J}{\partial o_{22}}\end{matrix}\right][∂bL+1∂J]=[∂b1∂J∂b2∂J]=[∂o11∂J+∂o21∂J∂o12∂J+∂o22∂J]
此矩阵每行的元素对于把∂J∂OUT\frac {\partial J}{\partial OUT}∂OUT∂J矩阵的每列元素相加。
总结：
可见，不论J(w)J(w)J(w)对www还是对bbb求偏导，都用到∂J∂OUT\frac {\partial J}{\partial OUT}∂OUT∂J。所以可以把此规律推广到h1=xw1+b~1h_1=xw_1+\tilde b_1h1=xw1+b~1,h2=Z1w2+b~2h_2=Z_1w_2+\tilde b_2h2=Z1w2+b~2等所有的线性连接层，可以通过其输出的∂J∂OUT\frac {\partial J}{\partial OUT}∂OUT∂J求出J(w)J(w)J(w)对www和对bbb的偏导数。如，对于第L-1层，有∂J∂WL=ZL−1T∂J∂hL\frac{\partial J}{\partial W_{L}}=Z_{L-1}^T\frac {\partial J}{\partial h_L}∂WL∂J=ZL−1T∂hL∂J。而前向传播的时候，ZL−1Z_{L-1}ZL−1已经求出来了，所以J(w)J(w)J(w)对本层权重矩阵www的梯度为上一层结果的转置ZL−1TZ_{L-1}^TZL−1T乘以权重矩阵后面一个矩阵的梯度∂J∂hL\frac {\partial J}{\partial h_L}∂hL∂J。
所以反向传播的时候，若要算权重矩阵www的梯度，还要用到其后面的矩阵的梯度∂J∂hL\frac {\partial J}{\partial h_L}∂hL∂J（因为ZL−1TZ_{L-1}^TZL−1T已知），而这是要求的。
求∂J∂hL\frac {\partial J}{\partial h_L}∂hL∂J：
根据最后一层：
OUT=ZLwL+1+b~L+1OUT=Z_Lw_{L+1}+\tilde b_{L+1}OUT=ZLwL+1+b~L+1
o11=z11w11+z12w21+z13w31+b1o_{11}=z_{11}w_{11}+z_{12}w_{21}+z_{13}w_{31}+b_1o11=z11w11+z12w21+z13w31+b1
o12=z11w12+z12w22+z13w32+b2o_{12}=z_{11}w_{12}+z_{12}w_{22}+z_{13}w_{32}+b_2o12=z11w12+z12w22+z13w32+b2
o21=z21w11+z22w21+z23w31+b1o_{21}=z_{21}w_{11}+z_{22}w_{21}+z_{23}w_{31}+b_1o21=z21w11+z22w21+z23w31+b1
o22=z21w12+z22w22+z23w32+b2o_{22}=z_{21}w_{12}+z_{22}w_{22}+z_{23}w_{32}+b_2o22=z21w12+z22w22+z23w32+b2
ZL=[z11z12z13z21z22z23]Z_L=\left[\begin{matrix}z_{11}&z_{12}&z_{13}\\z_{21}&z_{22}&z_{23}\end{matrix}\right]ZL=[z11z21z12z22z13z23]
对ZZZ求偏导：
∂J∂z11=∂J∂o11w11+∂J∂o12w12\frac{\partial J}{\partial z_{11}}=\frac{\partial J}{\partial o_{11}}w_{11}+\frac{\partial J}{\partial o_{12}}w_{12}∂z11∂J=∂o11∂Jw11+∂o12∂Jw12，∂J∂z12=∂J∂o11w21+∂J∂o12w22\frac{\partial J}{\partial z_{12}}=\frac{\partial J}{\partial o_{11}}w_{21}+\frac{\partial J}{\partial o_{12}}w_{22}∂z12∂J=∂o11∂Jw21+∂o12∂Jw22,
∂J∂z13=∂J∂o11w31+∂J∂o12w32\frac{\partial J}{\partial z_{13}}=\frac{\partial J}{\partial o_{11}}w_{31}+\frac{\partial J}{\partial o_{12}}w_{32}∂z13∂J=∂o11∂Jw31+∂o12∂Jw32
∂J∂z21=∂J∂o21w11+∂J∂o22w12\frac{\partial J}{\partial z_{21}}=\frac{\partial J}{\partial o_{21}}w_{11}+\frac{\partial J}{\partial o_{22}}w_{12}∂z21∂J=∂o21∂Jw11+∂o22∂Jw12，∂J∂z22=∂J∂o21w21+∂J∂o22w22\frac{\partial J}{\partial z_{22}}=\frac{\partial J}{\partial o_{21}}w_{21}+\frac{\partial J}{\partial o_{22}}w_{22}∂z22∂J=∂o21∂Jw21+∂o22∂Jw22,
∂J∂z23=∂J∂o21w31+∂J∂o22w32\frac{\partial J}{\partial z_{23}}=\frac{\partial J}{\partial o_{21}}w_{31}+\frac{\partial J}{\partial o_{22}}w_{32}∂z23∂J=∂o21∂Jw31+∂o22∂Jw32
写成矩阵：
[∂J∂z11∂J∂z12∂J∂z13∂J∂z21∂J∂z22∂J∂z23]=[∂J∂o11∂J∂o12∂J∂o21∂J∂o22][w11w21w31w12w22w32]\left[\begin{matrix}\frac{\partial J}{\partial z_{11}}&\frac{\partial J}{\partial z_{12}}&\frac{\partial J}{\partial z_{13}}\\\frac{\partial J}{\partial z_{21}}&\frac{\partial J}{\partial z_{22}}&\frac{\partial J}{\partial z_{23}}\end{matrix}\right]=\left[\begin{matrix}\frac{\partial J}{\partial o_{11}}&\frac{\partial J}{\partial o_{12}}\\\frac{\partial J}{\partial o_{21}}&\frac{\partial J}{\partial o_{22}}\end{matrix}\right]\left[\begin{matrix}w_{11}&w_{21}&w_{31}\\w_{12}&w_{22}&w_{32}\end{matrix}\right][∂z11∂J∂z21∂J∂z12∂J∂z22∂J∂z13∂J∂z23∂J]=[∂o11∂J∂o21∂J∂o12∂J∂o22∂J][w11w12w21w22w31w32]
所以：
∂J∂ZL=∂J∂OUTWL+1T\frac{\partial J}{\partial Z_L}=\frac{\partial J}{\partial OUT}W_{L+1}^T∂ZL∂J=∂OUT∂JWL+1T
(WL+1=[w11w12w21w22w31w32]W_{L+1}=\left[\begin{matrix}w_{11}&w_{12}\\w_{21}&w_{22}\\w_{31}&w_{32}\end{matrix}\right]WL+1=⎣⎡w11w21w31w12w22w32⎦⎤)
这样，在式子OUT=ZLwL+1+b~L+1OUT=Z_Lw_{L+1}+\tilde b_{L+1}OUT=ZLwL+1+b~L+1中：
∂J∂WL+1=ZLT∂J∂OUT\frac{\partial J}{\partial W_{L+1}}=Z_L^T\frac {\partial J}{\partial OUT}∂WL+1∂J=ZLT∂OUT∂J
∂J∂ZL=∂J∂OUTWL+1T\frac{\partial J}{\partial Z_L}=\frac{\partial J}{\partial OUT}W_{L+1}^T∂ZL∂J=∂OUT∂JWL+1T
WL+1W_{L+1}WL+1（可以用梯度下降更新）和ZLZ_LZL的梯度都有了。
但是ZLZ_LZL和hLh_LhL之间有个非线性变换fLf_LfL，如果可以通过非线性变换fLf_LfL求出∂J∂hL\frac{\partial J}{\partial h_{L}}∂hL∂J，这样就可以在反向传播的时候使用hLh_LhL的梯度∂J∂hL\frac{\partial J}{\partial h_{L}}∂hL∂J求解权重矩阵www的梯度∂J∂WL\frac{\partial J}{\partial W_{L}}∂WL∂J：
∂J∂WL=ZL−1T∂J∂hL\frac{\partial J}{\partial W_{L}}=Z_{L-1}^T\frac {\partial J}{\partial h_L}∂WL∂J=ZL−1T∂hL∂J
下面求损失函数对hLh_LhL的梯度∂J∂hL\frac{\partial J}{\partial h_{L}}∂hL∂J
非线性变换fLf_LfL常见的函数有3种：
1. 非线性变换fLf_LfL为Sigmoid函数
若fLf_LfL为Sigmoid函数，则：
ZL=Sigmoid(hL)=11+e−hLZ_L=Sigmoid(h_L)=\frac {1}{1+e^{-h_L}}ZL=Sigmoid(hL)=1+e−hL1
∂J∂hL=∂J∂ZLdZLdhL=∂J∂ZLe−hL(1+e−hL)2=∂J∂ZL1(1+e−hL)2e−hL(1+e−hL)2=∂J∂ZLZL(1−ZL)\frac {\partial J}{\partial h_L}=\frac {\partial J}{\partial Z_L}\frac{dZ_L}{dh_L}=\frac {\partial J}{\partial Z_L}\frac{e^{-hL}}{(1+e^{-h_L})^2}=\frac {\partial J}{\partial Z_L}\frac{1}{(1+e^{-h_L})^2}\frac{e^{-hL}}{(1+e^{-h_L})^2}=\frac {\partial J}{\partial Z_L}Z_L(1-Z_L)∂hL∂J=∂ZL∂JdhLdZL=∂ZL∂J(1+e−hL)2e−hL=∂ZL∂J(1+e−hL)21(1+e−hL)2e−hL=∂ZL∂JZL(1−ZL)
即∂J∂hL\frac{\partial J}{\partial h_{L}}∂hL∂J可以用ZLZ_LZL来表示：
∂J∂hL=∂J∂ZLZL(1−ZL)\frac {\partial J}{\partial h_L}=\frac {\partial J}{\partial Z_L}Z_L(1-Z_L)∂hL∂J=∂ZL∂JZL(1−ZL)
由于JJJ是标量，上式表示对矩阵中所有元素都进行这样的计算，所以得到的∂J∂hL\frac{\partial J}{\partial h_{L}}∂hL∂J维度同
2. 非线性变换fLf_LfL为tanh(双曲正切)函数
若fLf_LfL为tanh函数，则：
ZL=tanh(hL)=ehL−e−hLehL+e−hLZ_L=tanh(h_L)=\frac{e^{h_L}-e^{-h_L}}{e^{h_L}+e^{-h_L}}ZL=tanh(hL)=ehL+e−hLehL−e−hL
∂J∂hL=∂J∂ZLdZLdhL=∂J∂ZL4(ehL+e−hL)2=∂J∂ZL[1−(ehL−e−hLehL+e−hL)2]=∂J∂ZL(1−ZL2)\frac {\partial J}{\partial h_L}=\frac {\partial J}{\partial Z_L}\frac{dZ_L}{dh_L}=\frac {\partial J}{\partial Z_L}\frac{4}{(e^{h_L}+e^{-h_L})^2}=\frac {\partial J}{\partial Z_L}[1-(\frac{e^{h_L}-e^{-h_L}}{e^{h_L}+e^{-h_L}})^2]\\=\frac {\partial J}{\partial Z_L}(1-Z_L^2)∂hL∂J=∂ZL∂JdhLdZL=∂ZL∂J(ehL+e−hL)24=∂ZL∂J[1−(ehL+e−hLehL−e−hL)2]=∂ZL∂J(1−ZL2)
即：
∂J∂hL=∂J∂ZL(1−ZL2)\frac {\partial J}{\partial h_L}=\frac {\partial J}{\partial Z_L}(1-Z_L^2)∂hL∂J=∂ZL∂J(1−ZL2)
写成这个形式的好处是，只要储存ZLZ_LZL即可，不需要储存hLh_LhL。
3. 非线性变换fLf_LfL为ReLU函数(Rectified Linear Unit,线性整流函数)
若fLf_LfL为ReLU函数，则：
ZL=ReLU(hL)={0，hL≤0hL，hL>0Z_L=ReLU(h_L)=\begin{cases}0，h_L\leq 0\\h_L，h_L>0\end{cases}ZL=ReLU(hL)={0，hL≤0hL，hL>0
∂J∂hL=∂J∂ZLdZLdhL={0，hL≤0∂J∂ZL，hL>0\frac {\partial J}{\partial h_L}=\frac {\partial J}{\partial Z_L}\frac{dZ_L}{dh_L}=\begin{cases}0，h_L\leq0\\\frac{\partial J}{\partial Z_L}，h_L>0\end{cases}∂hL∂J=∂ZL∂JdhLdZL={0，hL≤0∂ZL∂J，hL>0
也是只要储存ZLZ_LZL即可，不需要储存hLh_LhL就可以求出∂J∂hL\frac {\partial J}{\partial h_L}∂hL∂J，从而继续往下进行反向传播。
扫一扫
5607
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
