上一篇写了反向传播算法在logistic回归中的应用,的确是杀鸡用牛刀,但是神经网络就相当于若干组logistic回归叠加在一起,这篇就开始对神经网络中的反向传播算法进行介绍和推导。
浅层神经网络
先来看看一个浅层神经网络,也就是只有一层隐藏层的神经网络(这里先以二分类为例)。
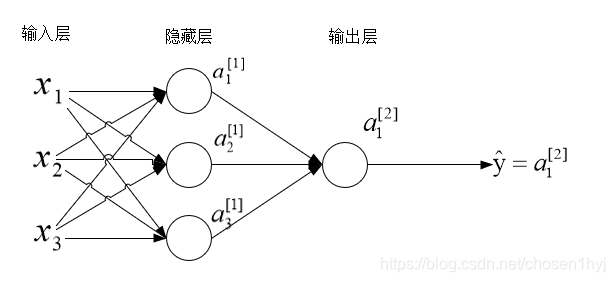
符号说明
x1,x2,x3x_1,x_2,x_3x1,x2,x3是一个输入样本的三个特征,a1[1]a_1^{[1]}a1[1]表示第一层的第一个激活单元。我们不把输入层包括在层数内,第一层从隐藏层开始计算,或者说,把输入层看做是第0层。在这里上标中括号里的数字表示层数,下标的数字表示从上到下数第几个单元,所以a2[1]a_2^{[1]}a2[1]就表示第一层第二个激活单元,a1[2]a_1^{[2]}a1[2]表示第二层第一个激活单元。预测值就是输出层的激活单元的值。这里再假设第l层有n[l]n^{[l]}n[l]个结点。
正向传播过程
有了前面logistic回归的基础,这里神经网络的正向传播过程也很容易。
先来看输入层到隐藏层的传播过程,先计算输入层到隐藏层第一个结点的输出,如下图所示:
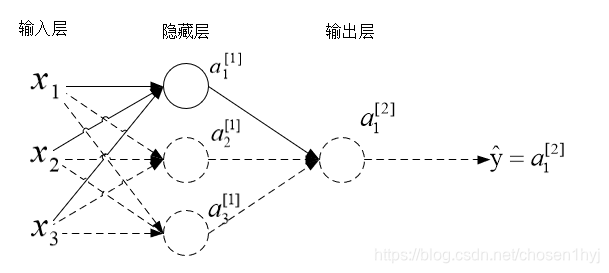
和logistic回归一样,这里输入层到隐藏层第一个结点的传播过程就应该是这样计算:
z1[1]=w1[1]Tx+b1[1]z_1^{[1]} = w_1^{[1]T}x + b_1^{[1]}z1[1]=w1[1]Tx+b1[1]
a1[1]=g(z1[1])a_1^{[1]} = g(z_1^{[1]})a1[1]=g(z1[1])
这里w1[1]w_1^{[1]}w1[1]表示输入层到隐藏层第一个结点的权重,是一个列向量,即维度是(n[1],1)(n^{[1]},1)(n[1],1),x=(x1,x2,x3)Tx=(x_1,x_2,x_3)^Tx=(x1,x2,x3)T。b1[1]b_1^{[1]}b1[1]表示作用在第一个激活单元上的偏置,是一个数。g(z)g(z)g(z)表示激活函数,g[1](z1[1])g^{[1]}(z_1^{[1]})g[1](z1[1])就是线性组合z1[1]z_1^{[1]}z1[1]通过第一层激活函数的结果。
这样一共可以写出三组方程:
z1[1]=w1[1]Tx+b1[1]z_1^{[1]} = w_1^{[1]T}x + b_1^{[1]}z1[1]=w1[1]Tx+b1[1]
a1[1]=g(z1[1])a_1^{[1]} = g(z_1^{[1]})a1[1]=g(z1[1])
z2[1]=w2[1]Tx+b2[1]z_2^{[1]} = w_2^{[1]T}x + b_2^{[1]}z2[1]=w2[1]Tx+b2[1]
a2[1]=g(z2[1])a_2^{[1]} = g(z_2^{[1]})a2[1]=g(z2[1])
z3[1]=w3[1]Tx+b3[1]z_3^{[1]} = w_3^{[1]T}x + b_3^{[1]}z3[1]=w3[1]Tx+b3[1]
a3[1]=g[1](z3[1])a_3^{[1]} = g^{[1]}(z_3^{[1]})a3[1]=g[1](z3[1])
这样我们就可以向量化:
[z1[1]z3[1]z3[1]]=[w1[1]Tw2[1]Tw3[1]T][x1x2x3]+[b1[1]b2[1]b3[1]]\left[ \begin{array}{l}
z_1^{[1]}\\
z_3^{[1]}\\
z_3^{[1]}
\end{array} \right] = \left[ \begin{array}{l}
w_1^{[1]T}\\
w_2^{[1]T}\\
w_3^{[1]T}
\end{array} \right]\left[ \begin{array}{l}
{x_1}\\
{x_2}\\
{x_3}
\end{array} \right] + \left[ \begin{array}{l}
b_1^{[1]}\\
b_2^{[1]}\\
b_3^{[1]}
\end{array} \right]⎣⎢⎡z1[1]z3[1]z3[1]⎦⎥⎤=⎣⎢⎡w1[1]Tw2[1]Tw3[1]T⎦⎥⎤⎣⎡x1x2x3⎦⎤+⎣⎢⎡b1[1]b2[1]b3[1]⎦⎥⎤
对应的有:
z[1]=W[1]x+b[1]{z^{[1]}} = {W^{[1]}}x + {b^{[1]}}z[1]=W[1]x+b[1]
a[1]=g[1](z[1])a^{[1]}=g^{[1]}(z^{[1]})a[1]=g[1](z[1])
检查一下维度:z[1]{z^{[1]}}z[1]是(n[1],1)(n^{[1]},1)(n[1],1),W[1]W^{[1]}W[1]是(n[1],n[0])(n^{[1]},n^{[0]})(n[1],n[0]),xxx是(n[0],1)(n^{[0]},1)(n[0],1),b[1]b^{[1]}b[1]是(n[1],1)(n^{[1]},1)(n[1],1)。确定没有问题。这就是输入层到隐藏层的正向传播过程。
再来看隐藏层到输出层的传播,就相当于一个递归的过程:
z[2]=W[2]a[1]+b[2]{z^{[2]}} = {W^{[2]}}a^{[1]} + {b^{[2]}}z[2]=W[2]a[1]+b[2]
a[2]=g[2](z[2])a^{[2]}=g^{[2]}(z^{[2]})a[2]=g[2](z[2])
我们现在将其推广到m个样本,和logistic回归类似,我们需要将这些向量横向排列,就可以非常方便地得到如下方程:
Z[1]=W[1]X+b[1]{Z^{[1]}} = {W^{[1]}}X + {b^{[1]}}Z[1]=W[1]X+b[1]
A[1]=g(Z[1])A^{[1]}=g(Z^{[1]})A[1]=g(Z[1])
Z[2]=W[2]A[1]+b[2]{Z^{[2]}} = {W^{[2]}}A^{[1]} + {b^{[2]}}Z[2]=W[2]A[1]+b[2]
A[2]=g[2](Z[2])A^{[2]}=g^{[2]}(Z^{[2]})A[2]=g[2](Z[2])
简要说明一下这些矩阵的维度,很好理解:
XXX就是将m个xxx横向排列得到的结果,所以其维度是(n[0],m)(n^{[0]},m)(n[0],m),Z[1]{Z^{[1]}}Z[1]的维度是(n[1],m)(n^{[1]},m)(n[1],m),而b[1]{b^{[1]}}b[1]的维度是(n[1],1)(n^{[1]},1)(n[1],1),这里用到了和之前logistic回归中一样的做法,利用Python的广播,可以将这一列加到相应矩阵对应的每一列中,所以这里也这么来表示即可。相应的A[1]{A^{[1]}}A[1]的维度也是(n[1],m)(n^{[1]},m)(n[1],m)。Z[2]{Z^{[2]}}Z[2]的维度是(n[2],m)(n^{[2]},m)(n[2],m),A[2]{A^{[2]}}A[2]的维度也是(n[2],m)(n^{[2]},m)(n[2],m),b[2]{b^{[2]}}b[2]的维度是(n[2],1)(n^{[2]},1)(n[2],1)。
反向传播过程
这个浅层神经网络的损失函数与logistic回归是一样的,代价函数也类似,只不过这里代价函数的参数有4个矩阵:
J(W[1],b[1],W[2],b[2])=1m∑i=1mL(y^,y)J({W^{[1]}},{b^{[1]}},{W^{[2]}},{b^{[2]}}) = \frac{1}{m}\sum\limits_{i = 1}^m {L(\hat y,y)}J(W[1],b[1],W[2],b[2])=m1i=1∑mL(y^,y)
上一篇的logistic回归的反向传播算法推导中,得到了相应的偏导,不妨再来回顾一下(先以一个样本为例):
da=−ya+1−y1−ada=- \frac{y}{a} + \frac{{1 - y}}{{1 - a}}da=−ay+1−a1−y,dz=da⋅g′(z)dz=da\cdot g'(z)dz=da⋅g′(z),dw=xdzdw=xdzdw=xdz,db=dzdb=dzdb=dz。
而二分类的浅层神经网络中,隐藏层到输出层之间的连接与logistics回归完全一致,因此,我们可以类比得到:
dz[2]=da[2]⋅g[2]′(z[2])dz^{[2]}=da^{[2]}\cdot g^{[2]'}(z^{[2]})dz[2]=da[2]⋅g[2]′(z[2]),输出层的激活函数为sigmoid函数,所以可以得到:
dz[2]=a[2]−ydz^{[2]}=a^{[2]}-ydz[2]=a[2]−y
dW[2]=dz[2]a[1]TdW^{[2]}=dz^{[2]}a^{[1]T}dW[2]=dz[2]a[1]T(这里与logistic回归不一致是因为W[2]W^{[2]}W[2]在构建的时候是将w1[2]w^{[2]}_1w1[2]给转置了,所以现在相当于这个等式整体转置了一下)
db[2]=dz[2]db^{[2]}=dz^{[2]}db[2]=dz[2]
隐藏层到输入层的反向传播中,dW[1]dW^{[1]}dW[1]和db[1]db^{[1]}db[1]是非常好求得的,因为类比logistic回归,这两个值的求解都依赖于dz[1]dz^{[1]}dz[1],所以有:
dW[1]=dz[1]xTdW^{[1]}=dz^{[1]}x^{T}dW[1]=dz[1]xT
db[1]=dz[1]db^{[1]}=dz^{[1]}db[1]=dz[1]
但是求解dz[1]dz^{[1]}dz[1]就比较麻烦了,因为求解dz[1]dz^{[1]}dz[1],就必须得到da[1]da^{[1]}da[1],而求解da[1]da^{[1]}da[1]与da[2]da^{[2]}da[2]不同,它有四个单元,对每个单元的求导都涉及到多个偏导分量的求和,我们不妨用链式法则,从头推导得到dz[1]dz^{[1]}dz[1],具体过程如下:
先以求LLL对z1[1]z^{[1]}_1z1[1]的偏导为例,根据链式法则,有:
∂L∂z1[1]=∂L∂a1[1]⋅da1[1]dz1[1]\frac{{\partial L}}{{\partial z_1^{[1]}}} = \frac{{\partial L}}{{\partial a_1^{[1]}}} \cdot \frac{{da_1^{[1]}}}{{dz_1^{[1]}}}∂z1[1]∂L=∂a1[1]∂L⋅dz1[1]da1[1]
而da1[1]dz1[1]=g[1]′(z1[1])\frac{{da_1^{[1]}}}{{dz_1^{[1]}}} = g^{[1]'}(z_1^{[1]})dz1[1]da1[1]=g[1]′(z1[1])
所以我们需要求得∂L∂a1[1]\frac{{\partial L}}{{\partial a_1^{[1]}}}∂a1[1]∂L。
根据链式法则:
∂L∂a1[1]=∂L∂z1[2]⋅dz1[2]da1[1]+∂L∂z2[2]⋅dz2[2]da1[1]+...+∂L∂zn[2][2]⋅dzn[2][2]da1[1]\frac{{\partial L}}{{\partial a_1^{[1]}}} = \frac{{\partial L}}{{\partial z_1^{[2]}}} \cdot \frac{{dz_1^{[2]}}}{{da_1^{[1]}}} + \frac{{\partial L}}{{\partial z_2^{[2]}}} \cdot \frac{{dz_2^{[2]}}}{{da_1^{[1]}}} + ... + \frac{{\partial L}}{{\partial z_{{n^{[2]}}}^{[2]}}} \cdot \frac{{dz_{{n^{[2]}}}^{[2]}}}{{da_1^{[1]}}}∂a1[1]∂L=∂z1[2]∂L⋅da1[1]dz1[2]+∂z2[2]∂L⋅da1[1]dz2[2]+...+∂zn[2][2]∂L⋅da1[1]dzn[2][2]
(注意,在这里,虽然这个简单神经网络的输出层只有一个单元,但是此证明是根据一般情况来说明的,即第2层有n[2]n^{[2]}n[2]个单元)
又有:
dz1[2]da1[1]=W11[2]\frac{{dz_1^{[2]}}}{{da_1^{[1]}}} = W_{11}^{[2]}da1[1]dz1[2]=W11[2]
dz2[2]da1[1]=W21[2]\frac{{dz_2^{[2]}}}{{da_1^{[1]}}} = W_{21}^{[2]}da1[1]dz2[2]=W21[2]
dzn[2][2]da1[1]=Wn[2]1[2]\frac{{dz_{{n^{[2]}}}^{[2]}}}{{da_1^{[1]}}} = W_{{n^{[2]}}1}^{[2]}da1[1]dzn[2][2]=Wn[2]1[2]
因此,有:
∂L∂a1[1]=∂L∂z1[2]⋅W11[2]+∂L∂z2[2]⋅W21[2]+...+∂L∂zn[2][2]⋅Wn[2]1[2]\frac{{\partial L}}{{\partial a_1^{[1]}}} = \frac{{\partial L}}{{\partial z_1^{[2]}}} \cdot W_{11}^{[2]} + \frac{{\partial L}}{{\partial z_2^{[2]}}} \cdot W_{21}^{[2]} + ... + \frac{{\partial L}}{{\partial z_{{n^{[2]}}}^{[2]}}} \cdot W_{{n^{[2]}}1}^{[2]}∂a1[1]∂L=∂z1[2]∂L⋅W11[2]+∂z2[2]∂L⋅W21[2]+...+∂zn[2][2]∂L⋅Wn[2]1[2]
用d Var来表示损失函数L对变量Var的偏导这种记法,就是:
da1[1]=dz1[2]⋅W11[2]+dz2[2]⋅W21[2]+...+dzn[2][2]⋅Wn[2]1[2]da_1^{[1]} = dz_1^{[2]} \cdot W_{11}^{[2]} + dz_2^{[2]} \cdot W_{21}^{[2]} + ... + dz_{{n^{[2]}}}^{[2]} \cdot W_{{n^{[2]}}1}^{[2]}da1[1]=dz1[2]⋅W11[2]+dz2[2]⋅W21[2]+...+dzn[2][2]⋅Wn[2]1[2]
我们可以很容易的对其进行向量化:
da1[1]=[W11[2],W21[2],...,Wn[2]1[2]][dz1[2]dz2[2]......dzn[2][2]]da_1^{[1]} = \left[ {W_{11}^{[2]},W_{21}^{[2]},...,W_{{n^{[2]}}1}^{[2]}} \right]\left[ \begin{array}{l} dz_1^{[2]}\\ dz_2^{[2]}\\ ......\\ dz_{{n^{[2]}}}^{[2]} \end{array} \right]da1[1]=[W11[2],W21[2],...,Wn[2]1[2]]⎣⎢⎢⎢⎡dz1[2]dz2[2]......dzn[2][2]⎦⎥⎥⎥⎤
这样,就可以得到:
dz1[1]=da1[1]⋅g[1]′(z1[1])=[W11[2],W21[2],...,Wn[2]1[2]][dz1[2]dz2[2]......dzn[2][2]]⋅g[1]′(z1[1])dz_1^{[1]} = da_1^{[1]} \cdot g^{[1]'}(z_1^{[1]}) = \left[ {W_{11}^{[2]},W_{21}^{[2]},...,W_{{n^{[2]}}1}^{[2]}} \right]\left[ \begin{array}{l}
dz_1^{[2]}\\
dz_2^{[2]}\\
......\\
dz_{{n^{[2]}}}^{[2]}
\end{array} \right] \cdot g^{[1]'}(z_1^{[1]})dz1[1]=da1[1]⋅g[1]′(z1[1])=[W11[2],W21[2],...,Wn[2]1[2]]⎣⎢⎢⎢⎡dz1[2]dz2[2]......dzn[2][2]⎦⎥⎥⎥⎤⋅g[1]′(z1[1])
同理,我们可以得到所有的 dzi[1]dz_i^{[1]}dzi[1]和dai[1]da_i^{[1]}dai[1],我们将 dzi[1]dz_i^{[1]}dzi[1]和dai[1]da_i^{[1]}dai[1]均纵向堆叠起来,可以得到:
[dz1[1]dz2[1]......dzn[1][1]]=[da1[1]da2[1]......dan[1][1]]∗[g[1]′(z1[1])g[1]′(z2[1])......g[1]′(zn[1][1])]\left[ \begin{array}{l} dz_1^{[1]}\\ dz_2^{[1]}\\ ......\\ dz_{{n^{[1]}}}^{[1]} \end{array} \right] = \left[ \begin{array}{l} da_1^{[1]}\\ da_2^{[1]}\\ ......\\ da_{{n^{[1]}}}^{[1]} \end{array} \right]*\left[ \begin{array}{l} g^{[1]'}(z_1^{[1]})\\ g^{[1]'}(z_2^{[1]})\\ ......\\ g^{[1]'}(z_{{n^{[1]}}}^{[1]}) \end{array} \right]⎣⎢⎢⎢⎡dz1[1]dz2[1]......dzn[1][1]⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡da1[1]da2[1]......dan[1][1]⎦⎥⎥⎥⎤∗⎣⎢⎢⎢⎡g[1]′(z1[1])g[1]′(z2[1])......g[1]′(zn[1][1])⎦⎥⎥⎥⎤
这里的“*”代表对应元素相乘。
再进一步向量化dai[1]da_i^{[1]}dai[1],有:
[da1[1]da2[1]......dan[1][1]]=[W11[2],W21[2],...,Wn[2]1[2]W12[2],W22[2],...,Wn[2]2[2]......W1n[2][2],W2n[2][2],...,Wn[2]n[2][2]][dz1[2]dz2[2]......dzn[2][2]]\left[ \begin{array}{l}
da_1^{[1]}\\
da_2^{[1]}\\
......\\
da_{{n^{[1]}}}^{[1]}
\end{array} \right] = \left[ \begin{array}{l}
W_{11}^{[2]},W_{21}^{[2]},...,W_{{n^{[2]}}1}^{[2]}\\
W_{12}^{[2]},W_{22}^{[2]},...,W_{{n^{[2]}}2}^{[2]}\\
......\\
W_{1{n^{[2]}}}^{[2]},W_{2{n^{[2]}}}^{[2]},...,W_{{n^{[2]}}{n^{[2]}}}^{[2]}
\end{array} \right]\left[ \begin{array}{l}
dz_1^{[2]}\\
dz_2^{[2]}\\
......\\
dz_{{n^{[2]}}}^{[2]}
\end{array} \right]⎣⎢⎢⎢⎡da1[1]da2[1]......dan[1][1]⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡W11[2],W21[2],...,Wn[2]1[2]W12[2],W22[2],...,Wn[2]2[2]......W1n[2][2],W2n[2][2],...,Wn[2]n[2][2]⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡dz1[2]dz2[2]......dzn[2][2]⎦⎥⎥⎥⎤
即da[1]=W[2]Tdz[2]d{a^{[1]}} = {W^{[2]T}}d{z^{[2]}}da[1]=W[2]Tdz[2]
dz[1]=W[2]Tdz[2]∗g[1]′(z[1])d{z^{[1]}} = {W^{[2]T}}d{z^{[2]}}*{g^{[1]}}^\prime ({z^{[1]}})dz[1]=W[2]Tdz[2]∗g[1]′(z[1])
(“*”表示对应元素相乘)
这样我们就推导了dz[1]d{z^{[1]}}dz[1]的表达式。不妨来检验一下维度,看看结果是否正确:
dz[1]dz^{[1]}dz[1]的维度是(n[1],1)(n^{[1]},1)(n[1],1),W[2]TW^{[2]T}W[2]T的维度是(n[1],n[2])(n^{[1]},n^{[2]})(n[1],n[2]),dz[2]dz^{[2]}dz[2]的维度是(n[2],1)(n^{[2]},1)(n[2],1),所以W[2]Tdz[2]{W^{[2]T}}d{z^{[2]}}W[2]Tdz[2]的维度就是(n[1],1)(n^{[1]},1)(n[1],1),而g[1]′(z[1]){g^{[1]}}^\prime ({z^{[1]}})g[1]′(z[1])的维度和z[1]z^{[1]}z[1]是一样的,也是(n[1],1)(n^{[1]},1)(n[1],1),因此,和W[2]Tdz[2]{W^{[2]T}}d{z^{[2]}}W[2]Tdz[2]对应元素相乘,维度依然是(n[1],1)(n^{[1]},1)(n[1],1)。完全正确。
这样我们就得到了浅层神经网络反向传播的重要方程(单个样本):
dz[2]=da[2]⋅g[2]′(z[2])dz^{[2]}=da^{[2]}\cdot g^{[2]'}(z^{[2]})dz[2]=da[2]⋅g[2]′(z[2]),输出层的激活函数为sigmoid函数,所以可以得到:
dz[2]=a[2]−ydz^{[2]}=a^{[2]}-ydz[2]=a[2]−y
dW[2]=dz[2]a[1]TdW^{[2]}=dz^{[2]}a^{[1]T}dW[2]=dz[2]a[1]T
db[2]=dz[2]db^{[2]}=dz^{[2]}db[2]=dz[2]
dW[1]=dz[1]xTdW^{[1]}=dz^{[1]}x^{T}dW[1]=dz[1]xT
db[1]=dz[1]db^{[1]}=dz^{[1]}db[1]=dz[1]
dz[1]=W[2]Tdz[2]∗g[1]′(z[1])d{z^{[1]}} = {W^{[2]T}}d{z^{[2]}}*{g^{[1]}}^\prime ({z^{[1]}})dz[1]=W[2]Tdz[2]∗g[1]′(z[1])
类似于logistic回归中的情况,我们现在可以将其推广到m个样本的情况中:
dZ[2]=A[2]−YdZ^{[2]}=A^{[2]}-YdZ[2]=A[2]−Y
dW[2]=1mdZ[2]A[1]TdW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T}dW[2]=m1dZ[2]A[1]T
db[2]=1mnp.sum(dZ[2],axis=1,keepdims=True)db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True)db[2]=m1np.sum(dZ[2],axis=1,keepdims=True) (这里用Python中numpy的函数来表示,更加方便,下面的db^{[1]}也一样,这里keepdims=True是为了让乘法结果的维度不会消失,依然保持为(n[2],1)(n^{[2]},1)(n[2],1),而不是numpy中的(n[2],)(n^{[2]},)(n[2],))
dW[1]=1mdZ[1]XTdW^{[1]}=\frac{1}{m}dZ^{[1]}X^{T}dW[1]=m1dZ[1]XT
db[1]=1mnp.sum(dZ[1],axis=1,keepdims=True)db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True)db[1]=m1np.sum(dZ[1],axis=1,keepdims=True)
有了这些方程,就可以再结合正向传播的过程,进行梯度下降了,梯度下降不再赘述。
深度神经网络
深度神经网络就是隐藏层数大于一的神经网络,比浅层神经网络多了若干层,其实大体上类似,公式可以类比得到。
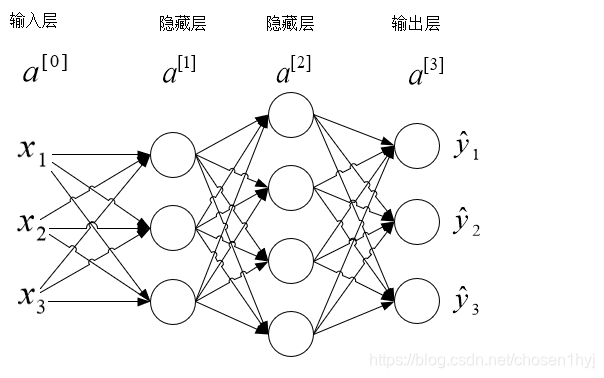
前向传播
由浅层神经网络的前向传播过程,我们可以直接得到深度神经网络的前向传播过程:
z[l]=W[l]a[l−1]+b[l]{z^{[l]}} = {W^{[l]}}a^{[l-1]} + {b^{[l]}}z[l]=W[l]a[l−1]+b[l]
a[l]=g[l](z[l])a^{[l]}=g^{[l]}(z^{[l]})a[l]=g[l](z[l])
这里依然以一个样本为例,其中lll表示第lll层。我们也很容易得到m个样本的结果:
Z[l]=W[l]A[l−1]+b[l]{Z^{[l]}} = {W^{[l]}}A^{[l-1]} + {b^{[l]}}Z[l]=W[l]A[l−1]+b[l]
A[l]=g[l](Z[l])A^{[l]}=g^{[l]}(Z^{[l]})A[l]=g[l](Z[l])
其中,lll的范围是[1,m]。
代价函数
这次,我们考虑更一般的情况,也就是多分类的情况。此时,损失函数为:
L(y,y^)=−∑k=1K[yklog(y^k)+(1−yk)log(1−y^k)]L(y,{\hat y})=- \sum\limits_{k = 1}^K {[{y_k}\log ({{\hat y}_k}) + (1 - {y_k})} \log (1 - {\hat y_k})]L(y,y^)=−k=1∑K[yklog(y^k)+(1−yk)log(1−y^k)]
在这里,y^k{{\hat y}_k}y^k表示y^{\hat y}y^的第k个元素。
如果标签y=[100]y = \left[ \begin{array}{l}
1\\
0\\
0
\end{array} \right]y=⎣⎡100⎦⎤
说明分类结果为第一个分类,
如果y=[010]y = \left[ \begin{array}{l}
0\\
1\\
0
\end{array} \right]y=⎣⎡010⎦⎤
说明分类结果为第二个分类,以此类推。用这样的方式来表示标签yyy。
对于m个样本来说,总的代价函数为:
J(W[l],b[l])=−1m∑i=1m∑k=1K[yk(i)log(y^k(i))]J({W^{[l]}},{b^{[l]}}) = - \frac{1}{m}\sum\limits_{i = 1}^m {\sum\limits_{k = 1}^K {[{y_k}^{(i)}\log (\hat y_k^{(i)}) }]}J(W[l],b[l])=−m1i=1∑mk=1∑K[yk(i)log(y^k(i))]
这实际上就是softmax回归了。
此时,代价函数的参数为WWW和bbb两组矩阵,每组有LLL个,也就是神经网络的层数。
反向传播
反向传播的过程和浅层神经网络也很类似,之前已经证明过相应的过程。
反向传播每一层的输入为da[l]da^{[l]}da[l],输出为da[l−1]da^{[l-1]}da[l−1],W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l],同时会产生dz[l]dz^{[l]}dz[l]
类似于浅层网络,我们可以得到通用的表达式如下(单个样本):
dz[l]=da[l]∗g[l]′(z[l])d{z^{[l]}} = d{a^{[l]}}*{g^{[l]'}}({z^{[l]}})dz[l]=da[l]∗g[l]′(z[l]) (“*” 表示对应元素相乘)
dW[l]=dz[l]⋅a[l−1]Td{W^{[l]}} = d{z^{[l]}} \cdot {a^{[l - 1]T}}dW[l]=dz[l]⋅a[l−1]T
db[l]=dz[l]d{b^{[l]}} = d{z^{[l]}}db[l]=dz[l]
da[l−1]=W[l]Tdz[l]d{a^{[l - 1]}} = {W^{[l]T}}{dz^{[l]}}da[l−1]=W[l]Tdz[l]
推广到m个样本中即为:
dZ[l]=dA[l]∗g[l]′(Z[l])d{Z^{[l]}} = d{A^{[l]}}*{g^{[l]'}}({Z^{[l]}})dZ[l]=dA[l]∗g[l]′(Z[l]) (“*” 表示对应元素相乘)
dW[l]=1mdZ[l]A[l−1]Td{W^{[l]}} = \frac{1}{m}d{Z^{[l]}}{A^{[l - 1]T}}dW[l]=m1dZ[l]A[l−1]T
db[l]=1mnp.sum(dZ[l],axis=1,keepdims=True)d{b^{[l]}} = \frac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims=True)db[l]=m1np.sum(dZ[l],axis=1,keepdims=True)
dA[l−1]=W[l]TdZ[l]d{A^{[l - 1]}} = {W^{[l]T}}{dZ^{[l]}}dA[l−1]=W[l]TdZ[l]
总结
在理解浅层神经网络的基础上,理解深度神经网络其实是非常容易的。在正向传播中,每一层都输入A[l−1]A^{[l-1]}A[l−1],输出A[l]A^{[l]}A[l],起始的输入为XXX。在反向传播过程中,每一层都输入dA[l]dA^{[l]}dA[l],输出dA[l−1]dA^{[l-1]}dA[l−1],W[l]W^{[l]}W[l]和b[l]b^{[l]}b[l],起始的输入为dA[L]dA^{[L]}dA[L],也就是代价函数关于最终输出值的导数,可以由代价函数的公式直接求得。一次正向传播加上一次反向传播后,就可以得到相应的梯度,进行一次梯度下降。
关于神经网络BP算法的记录就到此结束,本文涉及到的代价函数均不包含正则项,如果加上正则项,只需要在每一项偏导后加上相应的值。








 本文深入解析了浅层与深度神经网络的正向与反向传播过程,详细介绍了反向传播算法在神经网络中的应用,包括损失函数、激活函数的导数计算及权重更新。
本文深入解析了浅层与深度神经网络的正向与反向传播过程,详细介绍了反向传播算法在神经网络中的应用,包括损失函数、激活函数的导数计算及权重更新。
















 5613
5613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








