B+树

https://www.cnblogs.com/lwhkdash/p/5313877.html

1.简介

B+-tree：是应文件系统所需而产生的一种B-tree的变形树。

一棵m阶的B+树和m阶的B树的差异在于：

1. 有n棵子树的节点中含有n个关键字； (而B 树是n棵子树有n-1个关键字)
2. 所有的叶子节点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3. 所有的非终端节点可以看成是索引部分，这些节点中仅含有其子树根节点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)

2.  为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

 2.1 B+-tree的磁盘读写代价更低

B+-tree的内部节点并没有指向关键字具体信息的指针。因此其内部节点相对B 树更小。

如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree（一个节点最多8个关键字）的内部节点需要2个盘快。而B+ 树内部节点只需要1个盘快。当需要把内部节点读入内存中的时候，B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

2.2 B+-tree的查询效率更加稳定

由于非终节点并不是最终指向文件内容的结点，而只是叶子节点中关键字的索引。

所以任何关键字的查找必须走一条从根节点到叶子节点的路。

所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

3.B+树的插入

3.1步骤

1. 若为空树，直接插入，此时也就是根节点；
2. 对于叶子节点：
   1. 根据key找叶子节点，对叶子节点进行插入操作。
   2. 插入后，如果当前节点key的个数不大于m-1，则插入就结束。
   3. 反之，将这个叶子节点分成左右两个叶子节点进行操作，
      1. 左叶子节点包含了前m/2个记录，
      2. 右节点包含剩下的记录key，
      3. 将第m/2+1个记录的key进位到父节点中（父节点必须是索引类型节点）；
      4. 进位到父节点中的key，左孩子指针向左节点，右孩子指针向右节点。
3. 针对索引结点：
   1. 如果当前节点key的个数小于等于m-1，插入结束。
   2. 反之，将这个索引类型节点分成两个索引节点，
      1. 左索引节点包含前(m-1)/2个数据，
      2. 右节点包含m-(m-1)/2个数据，
      3. 然后将第m/2个key父节点中，
      4. 进位到父节点的key，左孩子指向左节点，父节点的key右孩子指向右节点。

下面以5阶B+树举例进行插入，根据B+树的定义，节点最多有4个值，最少有2个值。

空树插入5，8，10，15：

插入16：

值个数=5，分裂，中间值10进位到父节点：

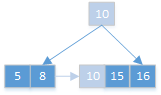
插入17，18：

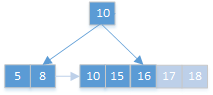
值个数=5，分裂，中间值16进位到父节点，节点值依16分开：

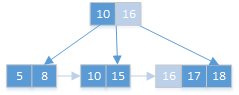
符合条件，插入完成。

4.B+树的删除

下面以5阶B+树举例进行删除，根据B+树的定义，节点最多有4个值，最少有2个值。

下面是初始状态

a）删除22，删除后个数为2，删除结束

b）删除15，结果如下：

删除之后，只有一个值，而兄弟有三个值，所以从兄弟节点借一个关键字，并更新索引节点

大家可以考虑删除7。我在这里直接给出结果

 

删除7之前的原始状态：

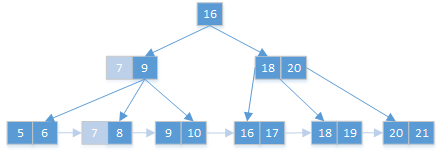
删除7之后：

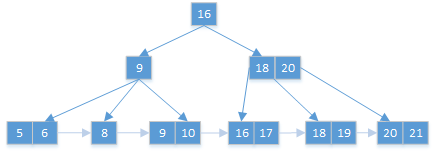
节点值个数不满足要求（>2），看兄弟节点有无多余节点可借：

• 节点9的兄弟节点（18，20）没有多余的节点；
• 节点8的兄弟节点（9，10）没有多余的节点；

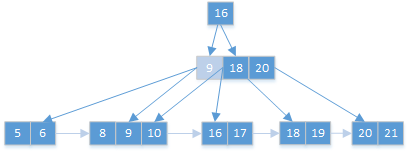
合并当前节点和兄弟节点：

先是节点9和兄弟节点合并：

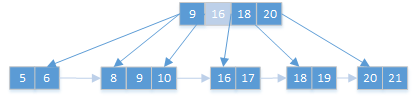
父节点16只有一个孩子节点（9，18，20），进行合并：

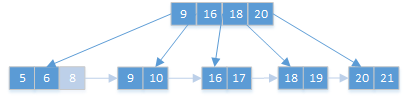
调整叶子节点：