《算法笔记》codeup_100000575_E

题目分析：

画出示意图就容易理解。

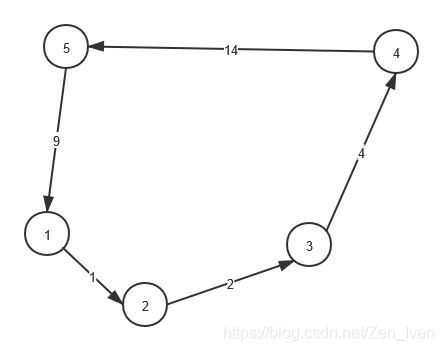
超时原因分析：

我原先的想法是先保存相邻两点之间距离，然后每次接收测试数据的输入后再用一个循环计算输入的两个出口之间的距离，这样就会出现如下两重循环的代码，从而导致超时。

	while(input_amount--) {                
                ......
		
		for(int i=exit_small; i<=exit_large-1; i++) {
			forward_distance += distance[i];
		}
                ......
	}

 后来再参考了别的大佬的解答后发现了这个造成超时的原因，改为在接收第一行的相邻出口距离的循环中，额外构造一个数组，保存每个出口到第一个出口的距离。这样计算任意两出口之间的距离，就只需要两出口到第一个出口的距离相减，不需要循环，从而减少了耗时。构造每个出口到第一个出口的距离数组的代码如下。

	int distance_near[100000];                                          //声明相邻两出口之间的距离 
	int distance_from_1[100000];                                        //声明第i个出口到第一个出口之间的距离 
	for(int i=1; i<=exits_amount; i++) {
		scanf("%d", &distance_near[i]);                                 //输入相邻两出口之间的距离
		distance_from_1[i+1] = distance_from_1[i] + distance_near[i];   //计算第i个出口到第一个出口之间的距离
		distance_sum += distance_near[i];                               //计算整个环形道路的总路程 
	}

完整解答：

#include <cstdio>
using namespace std;

int main() {
	int exits_amount, distance_sum, input_amount = 0;
	
	scanf("%d", &exits_amount);                                         //输入出口的个数 
	
	int distance_near[100000];                                          //声明相邻两出口之间的距离 
	int distance_from_1[100000];                                        //声明第i个出口到第一个出口之间的距离 
	for(int i=1; i<=exits_amount; i++) {
		scanf("%d", &distance_near[i]);                                 //输入相邻两出口之间的距离
		distance_from_1[i+1] = distance_from_1[i] + distance_near[i];   //计算第i个出口到第一个出口之间的距离
		distance_sum += distance_near[i];                               //计算整个环形道路的总路程 
	}
	
	scanf("%d", &input_amount);                                         //输入测试例子数 
	
	int a, b, exit_small, exit_large;
	int forward_distance, backward_distance;                            //声明顺序距离、逆序距离 
	while(input_amount--) {                
		scanf("%d %d", &a, &b);                                         //输入两个出口的的序号 
		exit_small = (a<b ? a:b);										//将序号按大小摆放 
		exit_large = (a>b ? a:b);
		
		forward_distance = 0;                                           //重置顺序距离、逆序距离
		backward_distance = 0;

		forward_distance = distance_from_1[exit_large] - distance_from_1[exit_small];    //计算顺序距离，值为相邻两出口各自到第一个出口的距离之差 
		backward_distance = distance_sum - forward_distance;             //计算逆序距离，值为总距离减顺序距离 
		if(forward_distance < backward_distance)                         //打印结果 
			printf("%d\n", forward_distance);
		else
			printf("%d\n", backward_distance);
	}
	
	return 0;
}