2022.02.11寻找两个正序数组的中位数

最新推荐文章于 2025-08-19 14:43:05 发布

范谦之

最新推荐文章于 2025-08-19 14:43:05 发布

阅读量226

点赞数

CC 4.0 BY-SA版权

文章标签：算法 java 蓝桥杯

本文链接：https://blog.youkuaiyun.com/Zack_zc_zc/article/details/123683367

这篇博客探讨了一种在O(log(m+n))时间复杂度内找到两个正序数组中位数的方法。通过转换问题为寻找第k大数字，利用二分查找优化了算法效率。代码示例展示了如何实现这一过程，适用于解决大规模数据的中位数查找问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2022.02.11寻找两个正序数组的中位数

（来源：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/ ）

题目描述

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为 O(log (m+n)) 。

输入格式

输出格式

样例输入

样例输出

数据规模和约定

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-10^6 <= nums1[i], nums2[i] <= 10^6

思路

根据题目，很容易得到一个O(m+n)的算法。即合并数组后使用二分查找。
但是，这里给出另一种解法可以将上题转换成在两个数组中寻找第k大数字。

在两个数组中查找第k大数字有如下算法：

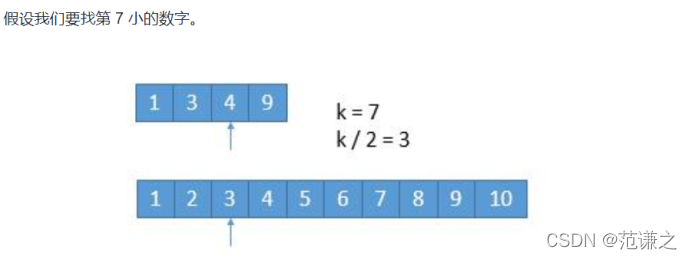
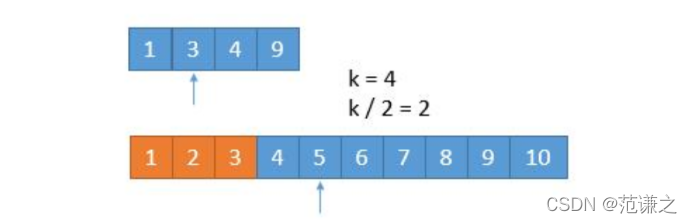
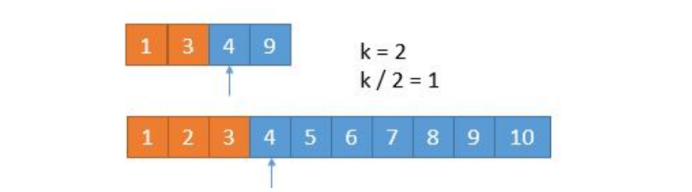
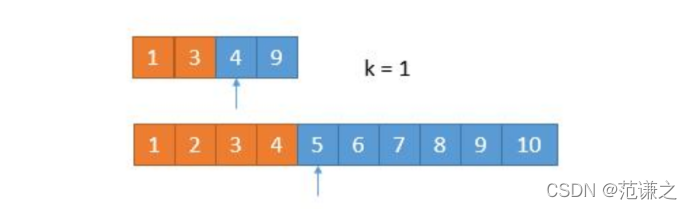
在这里插入图片描述

故可以log(k)的复杂度查找目标。

代码

	double findMedianSortedArrays(int[] a, int[] b) {
		int tol = a.length + b.length;
		if(tol % 2 == 0) return (double)(findKth(a, b, tol/2)+findKth(a, b, tol/2+1))/2;
		else return findKth(a, b, tol/2);
    }
	double findKth(int[] a, int[] b, int k) { // 0 1 2    len==3
		int sa = 0, sb = 0;
		while(true) {
			if(sa == a.length) return b[sb+k-1];
			if(sb == b.length) return a[sa+k-1];
			if(k == 1) return Math.min(a[sa], b[sb]);
			
			int cnt = k / 2;
			int na = Math.min(a.length, cnt+sa)-1;
			int nb = Math.min(b.length, cnt+sb)-1;
			int t1 = a[na], t2 = b[nb];
			if(t1 <= t2) {
				k -= na-sa+1;
				sa = na+1;
			} else {
				k -= nb-sb+1;
				sb = nb+1;
			}
		}
	}