2022.03.14摆花

最新推荐文章于 2025-12-18 17:00:31 发布

原创最新推荐文章于 2025-12-18 17:00:31 发布 · 194 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #蓝桥杯 #java

这篇博客讨论了一种背包问题的变体，即如何计算在不超过限制的情况下，有多少种方式可以将不同数量的花朵进行排列。作者通过动态规划的方法，定义了状态dp[i][j]表示前i种花可以组成j朵的方案数，并给出了状态转移方程。代码实现中，博主初始化了状态，并通过三层循环更新dp矩阵，最终输出了dp[n][m]的值，即所有花排列的方案数。

在这里插入图片描述

思路

联想到背包问题，即将每种花看成一个物体，将其装入到背包中，对于每个物体（每种花）可以装如0~a[i]个。
定义状态：dp[i][j]前i种花摆j朵的方案
状态转移：
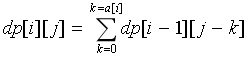
在这里插入图片描述
每种花的容量为k（装入的朵数），价值为种数。根据价值的定义不同，所以才有了不同的转移方程?

注意：
1)由于dp[i][j]可以从dp[i-1][0]转换得到，也算一种情况，所以如果按照上面直接求和算dp[i-1][0]的值应该为1.
2)根据上句，dp[0][0] == 1，满足dp[1][j>a[1]] == 0
3)或者定义初始状态时，可以模拟加入第一种花的所有dp状态，之后从第二种花开始遍历。

代码

	int n,m;
	int[] a = new int[300010];
	int[][] dp = new int[1001][1001];
	int MOD = 1000007;
	void test() throws IOException  {
		Reader cin = new Reader();
		n = cin.nextInt();
		m = cin.nextInt();
		for(int i = 1; i <= n; i++) a[i] = cin.nextInt();
		// 定义边界
//		for(int i = 0; i <= a[1]; i++) dp[1][i] = 1;
		dp[0][0] = 1;
		
		for(int i = 1; i <= n; i++) {
			for(int j = 0; j <= m; j++) {
				for(int k = 0; j-k>=0 && k <= a[i]; k++) { // k表示第i个物体取得个数
					dp[i][j] = (dp[i][j] + dp[i-1][j-k])%MOD;
				}
			}
		}	
		
		System.out.println(dp[n][m]);
	}