atcoder ABC437 题解

前言

最近的 abc 越来越水了，题目里面有很多已经见过的内容。

A - Feet

题目描述

1 英尺 = 12 英寸，请问 A 英尺 B 英寸总共是多少英寸？

解题思路

把英尺乘以 12 转化成英寸，和 B 相加即可。

代码

#include <bits/stdc++.h>

using namespace std;

int a, b;

int main()
{
    cin >> a >> b;
    cout << a * 12 + b;
    return 0;
}

B - Tombola

题目描述

现有一个 H 行 W 列的网格。网格的每个方格内都写有一个整数，且所有整数互不相同。其中，从上往下数第 $i$ 行、从左往右数第 $j$ 列的方格内的整数记为 $A_{i,j}$。

主持人依次报出了 N 个互不相同的整数 $B_1,B_2,\dots ,B_N$。

请你统计网格中每一行包含了多少个主持人报出的整数，求这些统计结果中的最大值。

解题思路

用一个数组来维护 B 数组中每一个数字出现的次数，然后逐行进行统计，累加计算统计次数。

代码

#include <bits/stdc++.h>

using namespace std;

const int maxn = 100;
int h, w, n, a[maxn][maxn], b[maxn];

int main()
{
    cin >> h >> w >> n;
    for (int i = 1; i <= h; i++)
        for (int j = 1; j <= w; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        b[x]++; // 出现次数
    }
    int fina_ans = 0;
    for (int i = 1; i <= h; i++) // 逐行统计
    {
        int ans = 0;
        for (int j = 1; j <= w; j++)
            ans += b[a[i][j]];
        fina_ans = max(fina_ans, ans);
    }
    cout << fina_ans;
    return 0;
}

C - Reindeer and Sleigh 2

题目描述

现有 $N$ 只驯鹿和一架雪橇。其中第 $i$ 只驯鹿的体重为 $W_i$，力量为 $P_i$。

需要为每一只驯鹿选择两种状态之一：「拉雪橇」或「乘雪橇」。

在此前提下，需满足一个条件：所有拉雪橇的驯鹿的总力量，必须大于或等于所有乘雪橇的驯鹿的总体重。

请问，最多可以让多少只驯鹿乘雪橇？

本题给定 $T$ 组测试用例，请你求解每一组测试用例的答案。

解题思路

这里我们可以维护 $\sum P-\sum W$ 的值（这里的 P 是所有正在拉雪橇的驯鹿的力量，W 是坐雪橇的驯鹿的体重），为了方便讨论我们令其为 D，一开始，我们让所有驯鹿都去拉雪橇，假设我们让第 $i$ 只驯鹿去坐雪橇（倒反天罡嘛不是），我们发现 D 变为 $D-P_i-W_i$，这里简单解释一下，因为这头驯鹿跑去坐车了，所以拉雪橇的 P 值之和减少 $P_i$，然后坐雪橇的 W 值之和增加 $W_i$，然后因为 D 里面是减法，所以 D 值的变化就是减少了 $P_i+W_i$。

那么我们就让 P + W 最小的驯鹿去坐雪橇就好，直到 D 小于零为止。

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 3e5 + 5;
int n, sum_p, sum[maxn];

void solve()
{
    sum_p = 0;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int w, p;
        cin >> w >> p;
        sum_p += p; // 这里的 sum_p 相当于 D
        sum[i] = w + p; // 只有力量和体重之和是有用的
    }
    sort(sum + 1, sum + n + 1); // 从小到大排序
    int ans = 0;
    for (int i = 1; i <= n; i++) // 让 sum 最小的那一批驯鹿去坐雪橇
    {
        sum_p -= sum[i];
        if (sum_p >= 0) // 不能再坐了
            ans++;
    }
    cout << ans << '\n';
    return;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int T;
    cin >> T; // 多组样例
    while (T--)
    {
        solve();
    }
    return 0;
}

D - Sum of Differences

题目描述

给定一个长度为 $N$ 的正整数序列 $A=(A_1,A_2,\dots ,A_N)$，以及一个长度为 $M$ 的正整数序列 $B=(B_1,B_2,\dots ,B_M)$。

请计算双重求和式 ${\sum }_{i=1}^N{\sum }_{j=1}^M|A_i-B_j|$ 的值，并将结果对 $998244353$ 取模。

补充说明：

• 符号说明：${\sum }_{i=1}^N$ 表示对 $i$ 从 1 到 $N$ 进行求和，双重求和即先对 $j$ 求和，再对 $i$ 求和；
• $|A_i-B_j|$ 表示 $A_i$ 与 $B_j$ 差值的绝对值；
• 取模（modulo）：即将计算结果除以 $998244353$ 后取其余数，保证结果在指定范围内。

解题思路

首先 A 数组中每一个元素的位置对于整道题来说没有影响，为了方便处理我们直接让 A 从小到大排序。然后我们发现，对于每一个 $B_i$ 来说，整个 A 数组被分成了两个部分，左半部分都是比 $B_i$ 小的，右半部分都是比 $B_i$ 大的。

这里我们可以先用二分查出两个部分的中间点，然后左右两边分别用前缀和处理出所有元素的和，这里设为 sum1 和 sum2，假设左半部分有 k 个，那么对于 $B_i$ 来说，A 数组中所有元素和它的差值的绝对值之和就是 $k\times B_i-sum1+sum2-(n-k)\times B_i$。

这样的话时间复杂度就是 $O(mlogn)$。

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int MOD = 998244353, maxn = 3e5 + 5; // 别忘了要取模
int n, m, a[maxn], sum[maxn], b[maxn];

signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i], a[i] %= MOD;
    for (int i = 1; i <= m; i++)
        cin >> b[i], b[i] %= MOD;
    sort(a + 1, a + n + 1); // 对 A 排序
    for (int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + a[i], sum[i] %= MOD; // 前缀和
    int ans = 0;
    for (int i = 1; i <= m; i++) // 对于每一个 B 元素都跑一次二分和前缀和求解
    {
        int mid = lower_bound(a + 1, a + n + 1, b[i]) - a; // lower_bound 偷懒，不用写二分了
        ans += (b[i] * (mid - 1) % MOD - sum[mid - 1] + MOD) % MOD, ans %= MOD; // 左半部分答案，这里要注意减法会出现负数
        ans += ((sum[n] - sum[mid - 1] + MOD) % MOD - b[i] * (n - mid + 1) % MOD + MOD) % MOD, ans %= MOD; // 右半部分求解
    }
    cout << ans;
    return 0;
}

E - Sort Arrays

题目描述

现有 $N+1$ 个序列 $A_0,A_1,\dots ,A_N$。其中，每个序列 $A_i$ 的定义如下：

• $A_0$ 是一个空序列。
• 对于 $1\le i\le N$，序列 $A_i$ 是通过在序列 $A_{x_i}$（满足 $0\le x_i<i$）的末尾追加一个整数 $y_i$ 得到的。

请找出一个长度为 $N$ 的排列 $P=(P_1,P_2,\dots ,P_N)$（该排列是 $(1,2,\dots ,N)$ 的一个重排），使其满足以下条件：

对于 $i=1,2,\dots ,N-1$，以下两个条件之一必须成立：

1. 序列 $A_{P_i}$ 字典序小于序列 $A_{P_{i+1}}$；
2. 序列 $A_{P_i}$ 与 $A_{P_{i+1}}$ 相等，且 $P_i<P_{i+1}$。

换句话说：将序列 $A_1,A_2,\dots ,A_N$ 按字典序进行排序（若存在多个相等的序列，则将索引更小的序列排在前面），排序后各序列对应的索引按顺序组成的序列即为排列 $P$。

补充说明:

• 排列：指将 $1$ 到 $N$ 的所有整数各出现一次且仅出现一次的序列；
• 字典序（lexicographical order）：类似字典中单词的排序规则，对于两个序列，从第一个元素开始依次比较，第一个出现不同元素的位置上，元素更小的序列整体字典序更小；若一个序列是另一个序列的前缀且长度更短，则短序列字典序更小；
• 索引：此处的索引即序列的下标 $1,2,\dots ,N$（对应 $A_1$ 到 $A_N$）。

解题思路

其实此题实现的是一个树形结构，这里我们以第一个样例举例子。

4
0 2
0 1
2 2
0 1

这样的话我们可以将其建成下面的树。

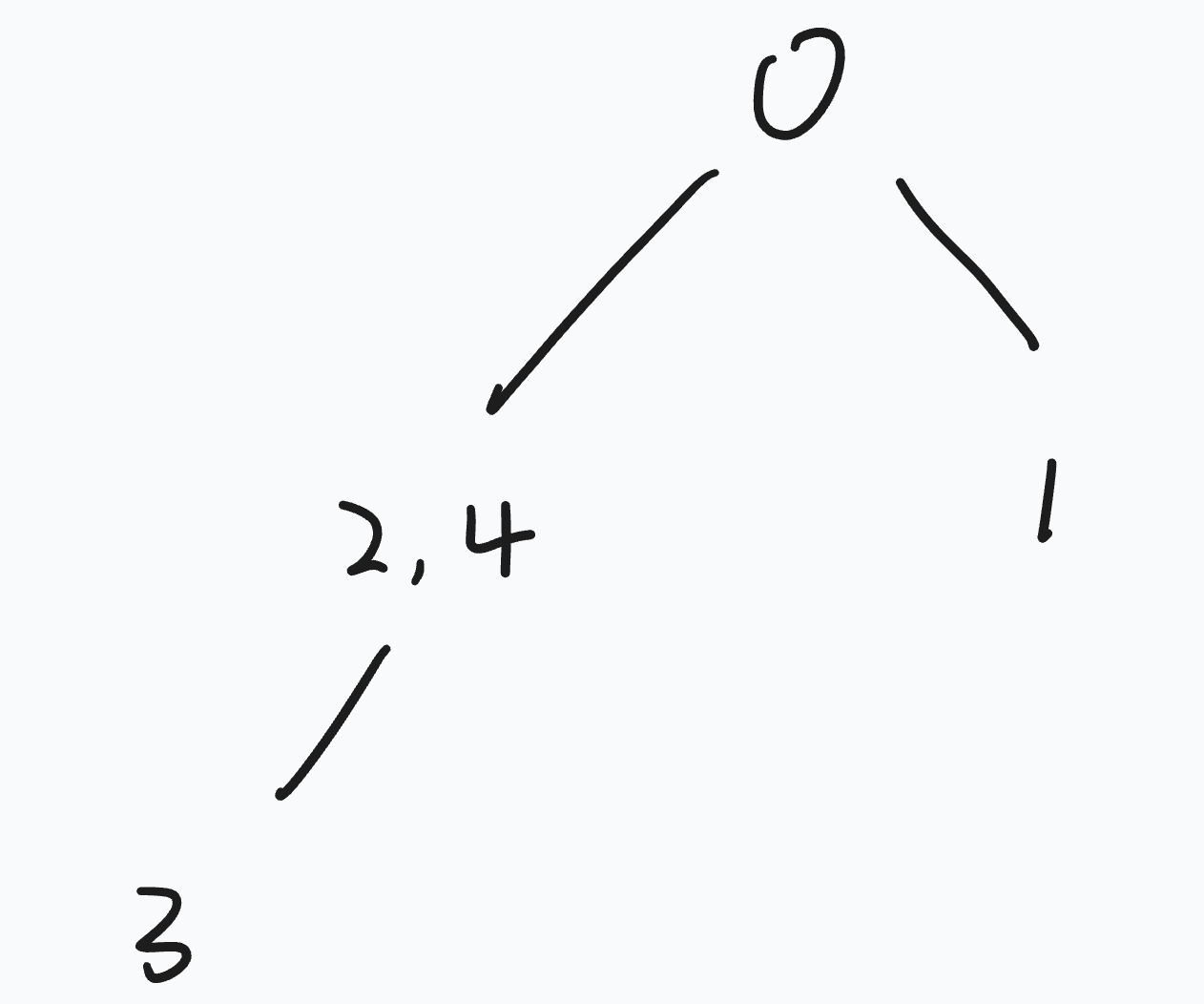
因为 2 和 4 一起接到 0 的下面（这里的数字指的是 A 数组的下标），并且二者在 $A_0$ 的基础上，加了一个相同的数字，所以我们可以将 $A_2{A}_4$ 放到同一个节点上。

建完树之后我们只需要进行一个先序遍历即可，建树的方法具体看代码。

代码

#include <bits/stdc++.h>

using namespace std;

const int maxn = 3e5 + 5;
int n, tot, pos[maxn];

struct node
{
    vector<int> idx; // 当前节点有几个序列，储存序列下标
    vector<pair<int, int>> son; // 储存儿子节点，first 里面存节点的值（不是每一次都是在一个已有元素后面加一个值嘛），second 存节点的编号
    unordered_map<int, int> M; // 相当于 vis，看看上面 son 里面出现过哪些值，这些值对应的节点编号是多少
} a[maxn];

void dfs(int cur) // 先序遍历输出结果
{
    if (cur != 1) // 1 号点存的是 A_0，不能输出
        for (int i = 0; i < a[cur].idx.size(); i++)
            cout << a[cur].idx[i] << ' ';
    for (int i = 0; i < a[cur].son.size(); i++)
        dfs(a[cur].son[i].second);
}

int main()
{
    cin >> n;
    a[++tot].idx.push_back(0);
    pos[0] = tot;
    for (int i = 1; i <= n; i++)
    {
        int fa, x;
        cin >> fa >> x;
        if (!a[pos[fa]].M[x]) // 如果这个值还没出现过，就新建一个点
        {
            a[pos[fa]].son.push_back({x, ++tot}); // 动态开点
            a[pos[fa]].M[x] = tot; // 维护下 M
            a[tot].idx.push_back(i);
            pos[i] = tot; // A_i 当前在节点 tot 里面
        }
        else // 如果出现过了就直接添加
        {
            int Poc = a[pos[fa]].M[x]; // 节点编号 
            a[Poc].idx.push_back(i); 
            pos[i] = Poc;
        }
    }
    for (int i = 1; i <= tot; i++) // 因为要求字典序从小到大，所以把每一个节点上的儿子按照值的大小进行排序
        sort(a[i].idx.begin(), a[i].idx.end()), sort(a[i].son.begin(), a[i].son.end());
    dfs(1);
    return 0;
}

F - Manhattan Christmas Tree 2

题目描述

在一个二维平面上有 $N$ 棵圣诞树。其中第 $i$ 棵圣诞树（$1\le i\le N$）的坐标为 $(X_i,Y_i)$。

给定 $Q$ 次查询，请按顺序处理每一次查询。查询分为以下两种类型：

• 类型 1：格式为 1 i x y。将第 $i$ 棵圣诞树的坐标修改为 $(x,y)$。
• 类型 2：格式为 2 L R x y。计算坐标 $(x,y)$ 到第 $L,L+1,\dots ,R$ 棵圣诞树中最远的那一棵的曼哈顿距离，并输出该距离。

其中，坐标 $(x_1,y_1)$ 和 $(x_2,y_2)$ 之间的曼哈顿距离定义为：
$$|x_1-x_2|+|y_1-y_2|$$

解题思路

假设对于某一次提问，坐标为 (x1, y1)，然后在二维平面上，有一棵圣诞树的坐标为 (x2, y2)，那么此时二者的曼哈顿距离的计算存在四种情况。

1. $x1\le x2,y1\le y2$：曼哈顿距离为 $x2-x1+y2-y1=(x2+y2)-(x1+y1)$；
2. $x1\le x2,y1\ge y2$：曼哈顿距离为 $x2-x1+y1-y2=(x2-y2)-(x1-y1)$；
3. $x1\ge x2,y1\le y2$：曼哈顿距离为 $x1-x2+y2-y1=(x1-y1)-(x2-y2)$;
4. $x1\ge x2,y1\ge y2$：曼哈顿距离为 $x1-x2+y1-y2=(x1+y1)-(x2+y2)$。

在我们求结果的时候 (x1 + y1) 和 (x1 - y1) 是固定的，所以如果我们需要求最大值的话，我们只需要维护所有圣诞树的 $(x+y)，(x-y)$ 的最大值和最小值就行了，一个线段树搞定，具体实现看代码。

代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 2e5 + 5, inf = 2e9 + 5;
int n, q, x[maxn], y[maxn];

struct tree
{
    int l, r;
    int max1, max2, min1, min2; // x + y 最大值、x - y 最大值、x + y 最小值、x - y 最小值
} t[maxn << 2];

void push_up(int x) // 每个节点用他们的儿子节点进行更新
{
    t[x].max1 = max(t[x * 2].max1, t[x * 2 + 1].max1);
    t[x].max2 = max(t[x * 2].max2, t[x * 2 + 1].max2);
    t[x].min1 = min(t[x * 2].min1, t[x * 2 + 1].min1);
    t[x].min2 = min(t[x * 2].min2, t[x * 2 + 1].min2);
}

void build(int u, int l, int r) // 建树
{
    t[u].l = l, t[u].r = r;
    if (l == r)
    {
        t[u].max1 = x[l] + y[l];
        t[u].max2 = x[l] - y[l];
        t[u].min1 = x[l] + y[l];
        t[u].min2 = x[l] - y[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(u * 2, l, mid);
    build(u * 2 + 1, mid + 1, r);
    push_up(u);
}

void update(int x, int pos, int new_x, int new_y)
{
    if (t[x].l == t[x].r) // 单点修改
    {
        t[x].max1 = new_x + new_y;
        t[x].max2 = new_x - new_y;
        t[x].min1 = new_x + new_y;
        t[x].min2 = new_x - new_y;
        return;
    }
    int mid = (t[x].l + t[x].r) >> 1;
    if (pos <= mid)
        update(x * 2, pos, new_x, new_y);
    else
        update(x * 2 + 1, pos, new_x, new_y);
    push_up(x);
}

struct info // 搞一个结构体用来在搜索线段树的时候储存答案
{
    int max1, max2, min1, min2; // 跟 tree 的含义差不多
    void clear()
    {
        max1 = max2 = -inf;
        min1 = min2 = inf;
    }
};

void query(int x, int l, int r, info &ans) // 带个指针存结果
{
    if (l <= t[x].l && r >= t[x].r)
    {
        ans.max1 = max(ans.max1, t[x].max1);
        ans.max2 = max(ans.max2, t[x].max2);
        ans.min1 = min(ans.min1, t[x].min1);
        ans.min2 = min(ans.min2, t[x].min2);
        return;
    }
    int mid = (t[x].l + t[x].r) >> 1;
    if (l <= mid)
        query(x * 2, l, r, ans);
    if (r > mid)
        query(x * 2 + 1, l, r, ans);
    return;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> x[i] >> y[i];
    build(1, 1, n);
    while (q--)
    {
        int type;
        cin >> type;
        if (type == 1)
        {
            int idx, new_x, new_y;
            cin >> idx >> new_x >> new_y;
            update(1, idx, new_x, new_y);
        }
        else
        {
            int L, R, q_x, q_y;
            cin >> L >> R >> q_x >> q_y;
            info ans;
            ans.clear();
            query(1, L, R, ans);
            int res1 = max(q_x + q_y - ans.min1, ans.max1 - (q_x + q_y)); // 计算答案
            int res2 = max(q_x - q_y - ans.min2, ans.max2 - (q_x - q_y));
            cout << max(res1, res2) << '\n';
        }
    }
    return 0;
}

G - Colorful Christmas Tree

题目描述

今年的圣诞季已然结束，转眼就到了新年时分。高桥正忙着大扫除，要把圣诞树收纳起来。

圣诞树上装饰着三种颜色的彩灯：红色、蓝色和绿色。整棵树共有 $N$ 盏彩灯，这些彩灯之间由 $N-1$ 条丝带相连。若将彩灯视作顶点、丝带视作边，那么这个结构对应一张树形图。

彩灯的编号为 $1$ 至 $N$，丝带的编号为 $1$ 至 $N-1$。其中，丝带 $i$ 连接彩灯 $u_i$ 和 $v_i$。彩灯的初始颜色规则如下：若 $c_i$ 为 $\text{R}$，则第 $i$ 盏灯初始为红色；若 $c_i$ 为 $\text{G}$，则初始为绿色；若 $c_i$ 为 $\text{B}$，则初始为蓝色。

高桥计划执行 $N-1$ 次下述操作，从而拆除所有丝带：

1. 从尚未拆除的丝带中，选择一条两端彩灯颜色不同的丝带并将其拆除。
2. 设被拆除丝带的两端彩灯为 $u$ 和 $v$，按照以下规则分别改变这两盏彩灯的颜色：
   • 若当前为红色，则变为绿色；
   • 若当前为绿色，则变为蓝色；
   • 若当前为蓝色，则变为红色。

请你判断高桥是否能通过重复上述操作拆除所有丝带。如果可以，输出一种可行的操作方案。

本题给定 $T$ 组测试用例，请你求解每一组测试用例。

解题思路

某位 NOI 金牌教了我一个贪心做法，但是我没听懂（dog）。

首先我们需要把树形结构转化为二分图来求解。首先，树作为无环连通图天然是二分图，我们可以通过 DFS 将所有节点划分为两个不相交的集合，保证每条树边的两个端点分属不同集合。题目要求每次拆除的丝带两端颜色必须不同，且拆除后两端颜色会按红→绿→蓝→红的循环规则变换，我们把颜色抽象为 0、1、2 三个状态。

接下来进行二分图最大流的建模，我们为每个原始节点构造 3 个状态点，分别对应红、绿、蓝三种初始颜色，二分图左部对应划分后其中一个集合的节点状态点，右部对应另一个集合的节点状态点。然后设置源点和汇点，源点向所有左部状态点连边，边权为这个点对应颜色的出现次数；所有右部状态点向汇点连边，规则和源点连边一致。对于每条树边对应的左部状态点和右部状态点，我们只在状态值不同的点之间连边，容量设为1，因为题目不是要求颜色不同嘛。

完成建模后，我们求解这个网络的最大流，若最大流的流量等于树边总数 $N-1$，则说明可以拆除所有丝带。此时我们可以从网络的满流边中提取操作方案，遍历左部的每个状态点，找到其出边中终点在右部且容量为 0 的满流边，解析出边的起点和终点对应的原始节点与状态值，记录每条树边两端的合法初始状态，最终就能得到一套可行的丝带拆除方案（最后我们 $n^2$ 求解即可）。

代码

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f

using namespace std;

const int maxn = 2050;
int n, c[maxn], side[maxn], cnt[3], tot, head[maxn * 3], d[maxn * 3], now[maxn * 3], c_u[maxn], c_v[maxn];
vector<pair<int, int>> e1[maxn * 2];

struct edge
{
    int nxt, v, w, id; // 终点、边权、是树上的哪一条边
} e2[50005];

void addedge(int u, int v, int w, int id) // 成对建边技巧
{
    e2[++tot].nxt = head[u];
    e2[tot].v = v;
    e2[tot].w = w;
    e2[tot].id = id;
    head[u] = tot;
    e2[++tot].nxt = head[v];
    e2[tot].v = u;
    e2[tot].w = 0;
    e2[tot].id = id;
    head[v] = tot;
}

void dfs(int x, int fa, int s) // 把所有的点分到左部或者右部
{
    side[x] = s;
    for (int i = 0; i < e1[x].size(); i++)
    {
        int v = e1[x][i].first;
        if (v == fa)
            continue;
        dfs(v, x, s ^ 1);
    }
    return;
}

bool bfs(int s, int t) //先建分层图
{
    queue<int> q;
    memset(d, 0, sizeof(d));
    q.push(s);
    d[s] = 1;
    now[s] = head[s];
    while (q.size())
    {
        int x = q.front();
        q.pop();
        for (int i = head[x]; i; i = e2[i].nxt)
        {
            int w = e2[i].w, v = e2[i].v;
            if (w > 0 && !d[v])
            {
                q.push(v);
                now[v] = head[v]; // 当前弧优化
                d[v] = d[x] + 1; // 分层图
                if (v == t)
                    return true;
            }
        }
    }
    return false;
}

int dinic(int x, int flow) // 我这个模版是从《算法竞赛进阶指南》这本书里学的，大家感兴趣的可以去看看
{
    if (x == 3 * n + 1)
        return flow;
    int rest = flow;
    for (int i = now[x]; i && rest; i = e2[i].nxt)
    {
        int v = e2[i].v, w = e2[i].w;
        now[x] = i;
        if (w && d[v] == d[x] + 1)
        {
            int k = dinic(v, min(rest, w));
            if (!k)
                d[v] = 0;
            e2[i].w -= k; // 反悔操作
            e2[i ^ 1].w += k;
            rest -= k;
        }
    }
    return flow - rest;
}

void get_Ans() // 在已经确定有解的情况下把操作流程提取出来
{
    int vis[maxn];
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++) 
        if (side[i] == 0)
            for (int j = 0; j < 3; j++)
            {
                int u = (i - 1) * 3 + j;
                for (int k = head[u]; k; k = e2[k].nxt)
                {
                    int v = e2[k].v, w = e2[k].w, id = e2[k].id;
                    if (w == 0 && id != 0) // 找到流量为 0 的边，说明被使用了
                    {
                        c_u[id] = u % 3; // id 这条边被删除的时候，两个点的状态
                        c_v[id] = v % 3;
                    }
                }
            }
    for (int t = 1; t < n; t++) // 找出 n - 1 个符合条件的边
    {
        int f = 1; // 还没找到
        for (int i = 1; i <= n && f; i++) // 枚举所有的边
        {
            for (int j = 0; j < e1[i].size() && f; j++)
            {
                int v = e1[i][j].first, id = e1[i][j].second;
                if (vis[id]) // 这个边已经被删除了，跳过
                    continue;
                if ((side[i] == 0 && c[i] == c_u[id] && c[v] == c_v[id]) ||
                    (side[i] == 1 && c[i] == c_v[id] && c[v] == c_u[id])) // 这条边相连的两点满足被删除时候的状态
                {
                    f = 0;
                    vis[id] = 1;
                    c[i] = (c[i] + 1) % 3; // 颜色变到下一个
                    c[v] = (c[v] + 1) % 3;
                    cout << id << ' '; // 直接输出答案
                    break;
                }
            }
        }
    }
    cout << '\n';
}

void solve()
{
    tot = 1; // 不能从 0 开始
    cin >> n;
    for (int i = 1; i <= n; i++) // 处理一下每一个点的颜色
    {
        char C;
        cin >> C;
        if (C == 'R')
            c[i] = 0;
        if (C == 'G')
            c[i] = 1;
        if (C == 'B')
            c[i] = 2;
        e1[i].clear();
    }
    for (int i = 1; i < n; i++) // 先把树建出来
    {
        int u, v;
        cin >> u >> v;
        e1[u].push_back({v, i});
        e1[v].push_back({u, i});
    }
    dfs(1, 0, 0); // 看看每一个点是属于二分图的左部还是右部
    for (int i = 0; i <= 3 * n + 1; i++)
        head[i] = 0;
    for (int i = 1; i <= n; i++) // 建二分图
    {
        int num = e1[i].size();
        cnt[c[i]] = (num + 2) / 3; // 每个点的三个状态出现的次数
        cnt[(c[i] + 1) % 3] = (num + 1) / 3;
        cnt[(c[i] + 2) % 3] = num / 3;
        if (side[i] == 0) // 源点和左部建边
        {
            addedge(3 * n, (i - 1) * 3, cnt[0], 0);
            addedge(3 * n, (i - 1) * 3 + 1, cnt[1], 0);
            addedge(3 * n, (i - 1) * 3 + 2, cnt[2], 0);
        }
        else // 汇点和右部建边
        {
            addedge((i - 1) * 3, 3 * n + 1, cnt[0], 0);
            addedge((i - 1) * 3 + 1, 3 * n + 1, cnt[1], 0);
            addedge((i - 1) * 3 + 2, 3 * n + 1, cnt[2], 0);
        }
    }
    for (int i = 1; i <= n; i++)
        if (side[i] == 0) // 从左部往右部建边
            for (int j = 0; j < e1[i].size(); j++)
            {
                int v = e1[i][j].first, id = e1[i][j].second;
                addedge((i - 1) * 3, (v - 1) * 3 + 1, 1, id); // 建的时候颜色不能相同
                addedge((i - 1) * 3, (v - 1) * 3 + 2, 1, id);
                addedge((i - 1) * 3 + 1, (v - 1) * 3, 1, id);
                addedge((i - 1) * 3 + 1, (v - 1) * 3 + 2, 1, id);
                addedge((i - 1) * 3 + 2, (v - 1) * 3, 1, id);
                addedge((i - 1) * 3 + 2, (v - 1) * 3 + 1, 1, id);
            }
    int flow = 0, max_flow = 0;
    while (bfs(3 * n, 3 * n + 1))
        while (flow = dinic(3 * n, inf))
            max_flow += flow;
    if (max_flow != n - 1)
    {
        cout << "No" << '\n';
        return;
    }
    cout << "Yes" << '\n';
    get_Ans();
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

本人能力有限，如有不当之处敬请指教！

除此之外，我建了一个 abc 刷题群，每周四免费讲解，感兴趣的朋友可以私信我。