Splay入门讲解

最新推荐文章于 2023-09-27 18:51:06 发布

原创最新推荐文章于 2023-09-27 18:51:06 发布 · 置顶 · 1.3k 阅读

11 ·

CC 4.0 BY-SA版权

Splay 专栏收录该内容

0 篇文章

订阅专栏

先安利一发，Splay入门解析【保证让你看不懂（滑稽）】
我就是看这个看懂的，这博客非常适合像我这种连平衡树都不知道是啥的蒟蒻。
另外，讲得不好还请见谅。

首先我们来看看平衡树是啥

平衡树首先是棵二叉搜索树，那么问题来了，二叉搜索树又是啥？

它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树----------百度百科

也就说，如图，二叉树中任意节点的权值大于左子树中的权值，小于右子树中的权值。
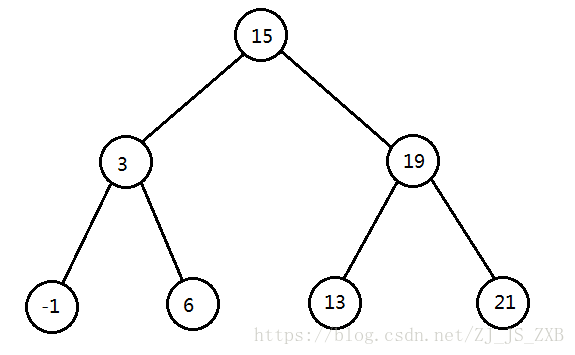
这里写图片描述
而平衡树，顾名思义，就是比较平衡,左右树的深度相差不大
但是，如何维护平衡树，使得它的深度较小呢？于是就有个叫Tarjan的大爷和另一个叫Sleator的大爷搞出来了一个splay

然后我们来看看splay的功能和时效

splay可以删除一个元素，插入一个元素，询问某元素的前驱或后继（前驱是指小于某元素的最大的元素，后继与之类似），将区间翻转，询问第k大的元素等等。
它的均摊复杂度是O(logN)的。
为什么说均摊复杂度呢，是因为splay这种东西不稳定，你如果按元素大小从小到大读入，它构成的树会退化成一条链。
像这样
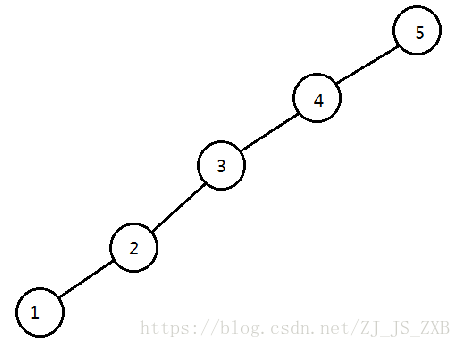
这里写图片描述
这时候查询的时效是O(N)的，但通过splay操作可以让树的节构趋向于平衡。

接着我们来看看splay的基本操作的

首先，作为一棵平衡树，想要提高效率就要维护树的稳定。为此，我们引入rotate操作，改变节点的顺序。
在这之前，我们先定义son[x][k]表示节点x的子节点，k=0时，表示左儿子，k=1时表示右儿子。fa[x]表示节点x的父节点。

如图
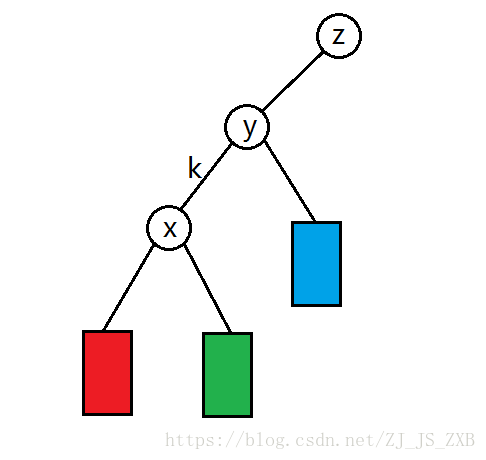
这里写图片描述
我们要使x旋转为z的子节点，这势必要使y变成x的子节点，但是x已经有子节点，怎么办？
很简单，把x的某个儿子过继给y不就好啦。
于是树就变成了这样。

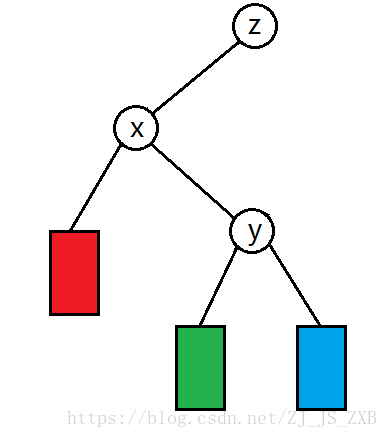
这里写图片描述

然后我们发现，树的性质并没有遭到破坏，说明旋转是可行的。
注意：被“过继”的儿子一点是x与y之间的儿子（看图理解一下）。
那到底发生了什么？
我们按从z到x的顺序来看。
son[z][0]由y变为x,fa[x]变为z。
son[y][0]由x变为绿色长方形，fa[绿色长方形]变为y。
son[x][1]由绿色长方形变为y，fa[y]变为x。
是不是看“绿色长方形”很不爽，我们尝试把它换掉。
设x为y的k儿子。0表示左，1表示右。
那绿色长方形就可以表示为son[x][k^1]（理性理解一下）。
所以，rotate的函数可以这么写。

// cnt[x]是节点x的元素的数量，size[x]是x的子树的cnt之和。后面会用到
inline void pushup(int x) {size[x]=size[son[x][0]]+size[son[x][1]]+cnt[x];}
inline void rotate(int x) {
	int y=fa[x],z=fa[y],k=son[y][1]==x;
	if (z) son[z][0]=x;
	son[y][0]=son[x][k^1],fa[son[x][k^1]]=y;
	son[x][k^1]=y,fa[y]=x,fa[x]=z;
	pushup(y),pushup(x);
}

这是旋转一个节点，那我们要将一个节点旋转到某节点的下方该怎么做？
我们自然而然就想到不断地将节点旋转旋转再旋转。
于是代码就是这样的：

inline void Splay(int x,int goal) {
	if (goal==0) root=x;
	while (fa[x]^goal) rotate(x);
}

然后你就会愉快地TLE了（也有可能水过去）。

为什么？

我们来看这种情况。

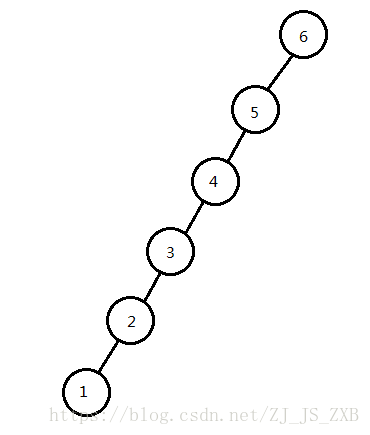
这里写图片描述

将2旋转到根。
按照代码操作，结果是这样的：

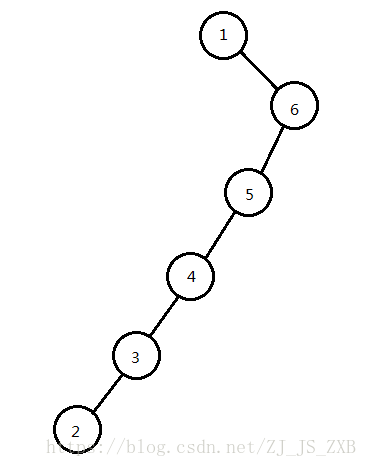
这里写图片描述

经过操作后，树的深度还是6，没有得到改善。假如每次询问最低的节点，询问复杂度都是O(N)的。
这就很尴尬。

那怎么解决这个问题？
我们就引入一个骚操作（双旋）：
当前节点为x，y为x的父节点，z为y的父节点。
x是y的k儿子，如果y也是z的k儿子，那我们就先旋转y，再旋转x。

于是就成了这样：

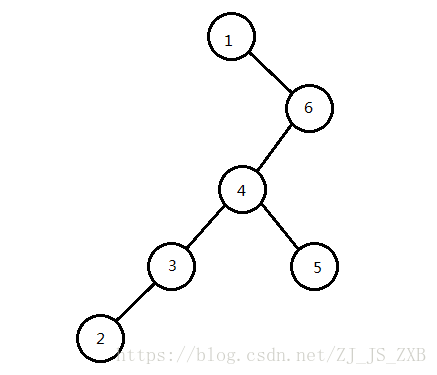
这里写图片描述

我们发现，树的深度减小了1。
但你肯定会说，这有什么卵用，才减小了一层，凭什么为这样就不会TLE？

我们来观察一下，树深度减小，是因为节点3与节点5处在了同一层，而之前节点5应该是节点3的爷爷。

为什么会这样？分析双旋的操作：

先旋转父节点，使爷爷节点和自己都成为父节点的孩子，此时父节点和自己处在同一层，原来的爷爷节点成为自己的父节点。

然后旋转自己，自己旋转方向的孩子节点成为自己现在父节点（原先爷爷节点）的孩子，也就是和自己原先父节点处在了同一层。
此处参考浅谈splay的双旋

这样就加快了splay的效率，使得均摊复杂度是O(logN)
所以代码就成了这样：

inline void Splay(int x,int goal) {
    if (goal==0) root=x;
    while (fa[x]^goal) {
        int y=fa[x],z=fa[y];
        if (z^goal) (son[y][1]==x)^(son[z][1]==y)?rotate(x):rotate(y);
        // 给自己提个醒，(z^goal)不要写成(z) QwQ
        rotate(x);
    }
}

我们再来看看splay的一些操作

我们先定义：
cnt[x]是节点x的元素的数量。
size[x]是x的子树的cnt之和。
val[x]是x的权值。

插入（Insert）
类似二分查找，比当前节点大搜索右子树，否则搜索左子树。
搜到相等的元素，元素个数直接加一，否则在开一个点。

inline void Insert(int x) {
    int u=root,ff=0;
    while (u&&val[u]^x) ff=u,u=son[u][x>val[u]];
    if (u) cnt[u]++;else {
        u=++tot;
        if (ff) son[ff][x>val[ff]]=u;
        val[u]=x,cnt[u]=1,size[u]=1;
        fa[u]=ff,son[u][0]=son[u][1]=0;
    }
    Splay(u,0);
}

查找元素x并把它splay到根（Find）
如果没有找到，会将一个权值与x相近的节点splay到根。

inline void Find(int x) {
    int u=root;
    if (!u) return;
    while (son[u][x>val[u]]&&val[u]^x) u=son[u][x>val[u]];
    Splay(u,0);
}

寻找元素x的前驱或后继（Next）

inline int Next(int x,bool f) {
// f=0时为求前驱，f=1时求后继
    Find(x);
    if (val[root]<x&&!f) return root;
    if (val[root]>x&& f) return root;
    int u=son[root][f];
    while (son[u][f^1]) u=son[u][f^1];
    return u;
}

删除（Delete）
找到元素x的前驱，把它Splay到根，找到x的后继，Splay到根的下方，你会发现，后继的左儿子就是x，且x无儿子，把它删除后不会对其他节点造成影响。

inline void Delete(int x) {
    int next=Next(x,1),last=Next(x,0);
    Splay(last,0),Splay(next,last);
    int u=son[next][0];
    if (--cnt[u]==0) son[next][0]=0,size[fa[next]]--;
    else Splay(u,0);
}

求第k大（K_th）

inline int K_th(int k) {
    int u=root;
    while (1) {
        int v=son[u][0];
        if (size[v]+cnt[u]<k)
            k-=size[v]+cnt[u],u=son[u][1];
        else
            if (size[v]>=k) u=v;
            else return val[u];
    }
}

模板题普通平衡树
AC代码：

#include<cstdio>
#include<string>
using namespace std;
const int maxn=1e5+6;
int N,opt,x,tot,root;
int cnt[maxn],size[maxn],fa[maxn],son[maxn][2],val[maxn];
inline int read() {
    int ret=0,f=1;char ch=getchar();
    for (; !isdigit(ch); ch=getchar()) if (ch=='-') f=-f;
    for (; isdigit(ch); ch=getchar()) ret=ret*10+ch-48;
    return ret*f;
}
inline void push_up(int x) {size[x]=size[son[x][0]]+size[son[x][1]]+cnt[x];}
inline void rotate(int x) {
    int y=fa[x],z=fa[y],k=son[y][1]==x;
    if (z) son[z][son[z][1]==y]=x;fa[x]=z;
    son[y][k]=son[x][k^1],fa[son[x][k^1]]=y;
    son[x][k^1]=y,fa[y]=x;
    push_up(y),push_up(x);
}
inline void Splay(int x,int goal) {
    if (goal==0) root=x;
    while (fa[x]^goal) {
        int y=fa[x],z=fa[y];
        if (z^goal) (son[y][1]==x)^(son[z][1]==y)?rotate(x):rotate(y);
        rotate(x);
    }
}
inline void Find(int x) {
    int u=root;
    if (!u) return;
    while (son[u][x>val[u]]&&val[u]^x) u=son[u][x>val[u]];
    Splay(u,0);
}
inline int Next(int x,bool f) {
    Find(x);
    if (val[root]<x&&!f) return root;
    if (val[root]>x&& f) return root;
    int u=son[root][f];
    while (son[u][f^1]) u=son[u][f^1];
    return u;
}
inline void Insert(int x) {
    int u=root,ff=0;
    while (u&&val[u]^x) ff=u,u=son[u][x>val[u]];
    if (u) cnt[u]++;else {
        u=++tot;
        if (ff) son[ff][x>val[ff]]=u;
        val[u]=x,cnt[u]=1,size[u]=1;
        fa[u]=ff,son[u][0]=son[u][1]=0;
    }
    Splay(u,0);
}
inline void Delete(int x) {
    int next=Next(x,1),last=Next(x,0);
    Splay(last,0),Splay(next,last);
    int u=son[next][0];
    if (--cnt[u]==0) son[next][0]=0,size[fa[next]]--;
    else Splay(u,0);
}
inline int K_th(int k) {
    int u=root;
    while (1) {
        int v=son[u][0];
        if (size[v]+cnt[u]<k)
            k-=size[v]+cnt[u],u=son[u][1];
        else
            if (size[v]>=k) u=v;
            else return val[u];
    }
}
int main() {
    N=read(),tot=0;
    Insert(-2147483647);
    Insert(+2147483647);
    for (int i=1; i<=N; i++) {
        opt=read(),x=read();
        if (opt==1) Insert(x);else
        if (opt==2) Delete(x);else
        if (opt==3) Find(x),printf("%d\n",size[son[root][0]]);else
        if (opt==4) printf("%d\n",K_th(x+1));else
        printf("%d\n",val[Next(x,opt==6)]);
    }
    return 0;
}