提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
MATLAB 仿真:不同阶数 QAM 的误码率分析
1. 引言
在无线通信系统中,调制方式的选择对系统的性能至关重要。其中,正交振幅调制 (QAM) 是一种常见的调制方式,被广泛用于现代数字通信系统。本篇博客将使用 MATLAB 对 4-QAM、16-QAM、64-QAM 和 256-QAM 的误码率 (BER) 进行仿真,并与理论结果进行对比。
2. 代码解析与仿真思路
2.1 代码概述
该 MATLAB 代码实现了不同阶数 (M) 的 QAM 调制,并在不同信噪比 (SNR) 下计算误码率。具体步骤如下:
- 设置 SNR 范围 (3dB 到 15dB)。
- 遍历不同阶数的 QAM (M = 4, 16, 64, 256)。
- 计算理论误码率。
- 进行 QAM 调制和解调。
- 在噪声信道中传输信号,并计算实际误码率。
- 绘制理论和实测误码率曲线。
2.2 代码分析
2.2.1 参数设置
clear all; close all; clc;
% SNR 范围 3dB 到 15dB,间隔 1dB
snr = 3:1:15;
M_values = [4, 16, 64, 256]; % 不同阶数的QAM
figure;
colors = ['b', 'r', 'g', 'm']; % 颜色数组
首先,我们定义了 SNR 范围,并选择 4 种不同阶数的 QAM。colors 数组用于绘图时区分不同的 QAM。
2.2.2 计算理论误码率
for m_idx = 1:length(M_values)
M = M_values(m_idx);
k = log2(M); % 每个符号携带的比特数
error_theory = (1-(1-(2*(1-1/sqrt(M))*1/2*erfc(1/sqrt(2)*sqrt(3*k*10.^(snr/10)/(M-1))))).^2)/k;
M代表 QAM 阶数。k = log2(M)计算每个符号携带的比特数。error_theory计算理论误码率,其公式来源于 QAM 在高斯白噪声 (AWGN) 信道下的误码率理论计算。
2.2.3 误码率仿真
error_bit = zeros(1, length(snr));
for i = 1:length(snr)
% 生成随机二进制数据
N = max(5000, min(floor(1./error_theory(i))*100 + 100, 1e6)); % 限制最大N
data = randi([0 1], 1, N*k); % 生成二进制数据
% QAM 调制
mod_data = qammod(bi2de(reshape(data, [], k)), M, 'UnitAveragePower', true);
N确保足够的采样数目,以保证误码率计算的可靠性。- 生成随机二进制数据流
data。 qammod用于 QAM 调制,并保证单位平均功率 (UnitAveragePower = true)。
% 添加噪声
rx_sig = awgn(mod_data, snr(i), 'measured');
% QAM 解调
demod_data = de2bi(qamdemod(rx_sig, M, 'UnitAveragePower', true), k);
awgn(mod_data, snr(i), 'measured')向调制信号mod_data添加噪声。qamdemod用于 QAM 解调,并恢复二进制数据。de2bi将解调后的符号数据转换回二进制格式。
% 误码率计算
error_bit(i) = sum(sum(demod_data ~= reshape(data, [], k))) / (N*k);
end
计算误码率,即错误比特数除以总比特数。
2.2.4 绘制误码率曲线
semilogy(snr, error_bit, ['-*', colors(m_idx)]);
hold on;
semilogy(snr, error_theory, ['-+', colors(m_idx)]);
semilogy采用对数坐标绘制误码率曲线。- 通过
hold on让不同 QAM 阶数的误码率曲线同时显示。
最终,添加图例、坐标轴标签和标题:
grid on;
legend('4-QAM 实测', '4-QAM 理论', '16-QAM 实测', '16-QAM 理论', '64-QAM 实测', '64-QAM 理论', '256-QAM 实测', '256-QAM 理论', 'Location', 'SouthWest');
xlabel('SNR (dB)');
ylabel('误码率');
title('不同阶数 QAM 误码率');
3. 仿真结果分析
运行 MATLAB 代码后,我们可以看到不同阶数 QAM 的误码率曲线。
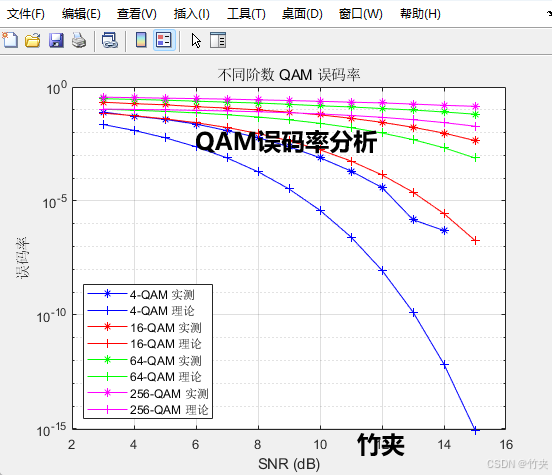
分析如下:
误码率随 SNR 增加而降低:SNR 越高,信号质量越好,误码率随之降低。
阶数越高,误码率越大:较高阶的 QAM (如 256-QAM) 承载更多比特,但抗噪声能力更差。
理论误码率和实测误码率吻合:验证了仿真方法的正确性。
4. 结论
本次实验通过 MATLAB 仿真分析了不同阶数 QAM 的误码率特性,并验证了理论计算的正确性。仿真结果表明,QAM 阶数越高,其误码率也随之增加,因此在实际应用中需要权衡数据速率与抗噪声能力。
5. 完整代码链接
https://m.tb.cn/h.60dEi1W?tk=41xBerZm4Zl























 3187
3187

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








