QR法求解特征值特征向量

一 QR原理

理论依据：任意一个非奇异矩阵（满秩的方阵）A都可以分解为一个正交矩阵Q和一个上三角矩阵R的乘积，且当R对角元符号确定时，分解是唯一的。QR分解是一种迭代方法，迭代格式如下：
当Ak基本收敛到为上三角矩阵时，迭代完成，此时主对角元素就是特征值。

特别地：当A是对称阵的时候，Ak是对角阵Λ，Q=Qk-1Qk-2…Q1就是其正交特征向量矩,有Q^TAQ=Ak=Λ，即A正交对角化与Ak。

如何理解？我们看下图公式:

所以，QR迭代过程从数学的角度来想其实就是不断正交化的过程。

二 QR算法步骤

1.Householder变换进行QR分解

反射矩阵：任取单位向量w,反射矩阵H=E-2WW^T ,显然HH^T =E，H是正交阵

定理：任取两个模长相等的的向量x,y，一定存在一个反射矩阵H，使得Hx=y，
此时w=(x-y)/(|x-y|)（向量的差除以向量差的模）

应用：现在我们取矩阵的一列为x,m=|x|,y=m*[1,0,0,…0]^T 根据上面的定理求出H，使得Hx=y,是不是通过正交变化就把那一列化成了[m,0,0,0]^T ,这样就达到了将下三角元素全化为0的效果。看下图，举个例子来说明QR分解过程：

看懂上述过程就知道，Householder变换是利用了反射定理，经过n-1轮正交变换，将下三角元素全部化为0，从而得到上三角矩阵R，将所有H矩阵左乘运算再转置得到正交矩阵Q，即A=QR

我们看看QR分解的代码：

#QR分解
def qrSplit(A):
    n=A.shape[0]#A的维度
    Q=[[]]
    R=A
    for i in range(0,n-1):
        B=R
        if i!=0:
            #删除一行一列,得n-1阶子阵
            B=B[i:,i:]
        #取第一列向量
        x=B[:,0]
        #向量摸长
        m=np.linalg.norm(x)
        #生成一个模长为m，其余项为0的向量y
        y=[0 for j in range(0,n-i)]
        y[0]=m
        #计算householder反射矩阵
        #w = (x-y)/||x-y||
        w=x-y
        w=w/np.linalg.norm(w)
        #H=E-2*WT*W
        H=np.eye(n-i)-2*np.dot(w.reshape(n-i,1),w.reshape(1,n-i))#H是个正交矩阵
        #第一次计算不需对正交正H升维
        if i==0: 
            #第一次迭代
            Q=H
            R=np.dot(H,R)
        else:
            #因为降了维度，所以要拼接单位矩阵
            D=np.c_[np.eye(i),np.zeros((i,n-i))]
            H=np.c_[np.zeros((n-i,i)),H]
            H=np.r_[D,H]
            #迭代计算正交矩阵Q和上三角R
            Q=np.dot(H,Q)
            R=np.dot(H,R)
    Q=Q.T
    return [Q,R]

我们测试一下QR分解后是否能还原：

A=np.array([1,2,3,4,2,1,2,3,3,2,1,2,4,3,2,1])
A=A.reshape(4,4)
print('A原来的样子')
print(A)
qr = qrSplit(A)
print('打印Q,R')
print(qr[0])
print(qr[1])
print('打印Q*R')
print(np.dot(qr[0],qr[1]))

很明显，R下三角元素都非常小，可以认为是0.

2.QR迭代

上一步完成了QR分解，QR迭代就非常简单了，看代码：

#QR迭代求特征值特征向量
def  qrEgis(A):
    # QR迭代(尽量让它多迭代几次，以至于AK收敛为上三角)
    qr = []
    n = A.shape[0]  # A的维度
    Q = np.eye(n)
    for i in range(0, 100):
        # A=QR
        qr = qrSplit(A)
        # 将Q右边边累成
        Q = np.dot(Q,qr[0])
        # A1=RQ
        A = np.dot(qr[1], qr[0])

    AK = np.dot(qr[0], qr[1])
    #把e取出来
    e=[]
    for i in range(0,n):
        e.append(AK[i][i])
    #对特征值按升序排序，特征向量与其对应
    for i in range(0,n-1):
        min=e[i]
        for j in range(i+1,n):
            if e[j]<min:
                min=e[j]
                #交换特征值
                tmp=e[i]
                e[i]=e[j]
                e[j]=tmp
                #交换特征向量
                r=np.copy(Q[:,i])
                Q[:,i]=Q[:,j]
                Q[:,j]=r;
    return [e,Q]

我们输入一个对称阵，同时去求出它的特征值与特征向量，测试一下。
并且与numpy自带的求解特征值、特征向量的做个对比，看代码：

A=np.array([1,2,3,4,2,1,2,3,3,2,1,2,4,3,2,1])
A=A.reshape(4,4)
egis =qrEgis(A)
print('自己写的QR分解')
print(egis[0]);
print('......')
print(egis[1]);
print('numpy自带的分解器')
e,u=np.linalg.eigh(A);
print(e)
print('.....')
print(u)

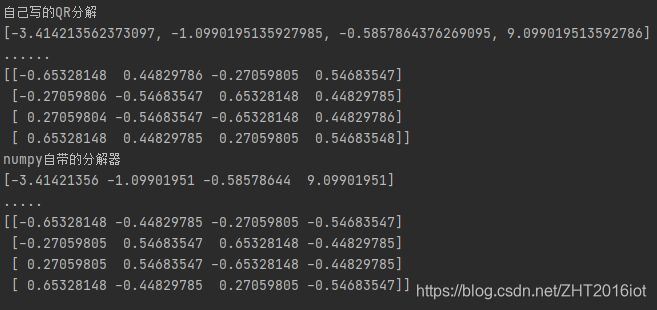
可以看出自己写的QR分解法和numpy自带的分解器求出的特征值是一样的。
特征向量在数值上一样，符号不一样并没有关系，因为X和-X都是A的特征向量。

注意：如果A不是对称阵，QR法只能求出全部特征值，不能同时求出特征向量。
但是，已知特征值求特征向量可以采用反幂法。
关于反幂法，学过数值分析的知道，其实也是一个迭代过程。