本文详细介绍了如何使用树莓派设计和制作二轮平衡小车，包括平衡车的动力学建模、PID控制器参数计算、CATIA结构设计、环境搭建以及代码编写与调试过程。内容涵盖受力分析、运动学和动力学方程、MATLAB的零极点绘制、硬件选型和组装、系统安装与配置、软件包安装与测试等关键步骤。
文章目录
树莓派平衡小车仿真、设计与制作
算法设计
1.平衡车动力学建模
1.1受力分析
首先将问题简化为二维平面倒立摆问题，以下为小车的模型图：
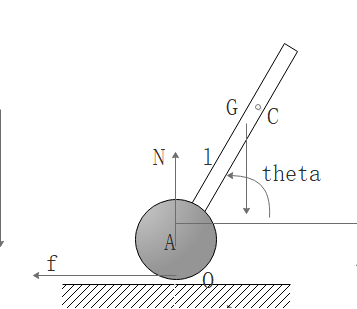
小车整体模型图
下面采用隔离法，分别对轮子部分及杆件部分进行分析，以下为轮子单独受力图：
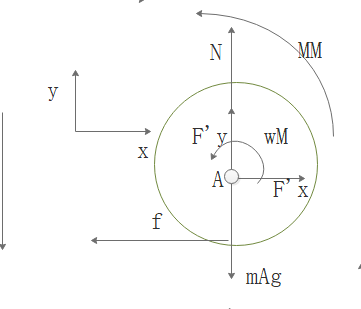
轮子部分单独受力分析
以下为杆件单独受力图：
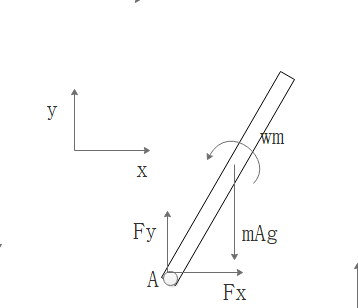
杆单独受力分析
1.2运动学分析
根据小车模型首先进行运动学分析，下面为轮子的速度分析：
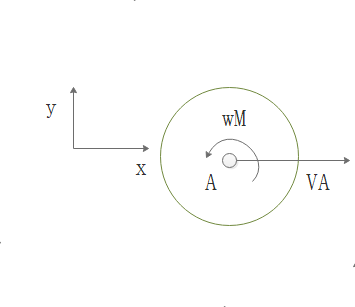
轮子速度分析
对杆件速度分析有：
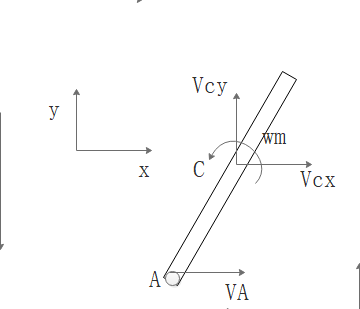
杆速度分析
在进行加速度分析轮子有：
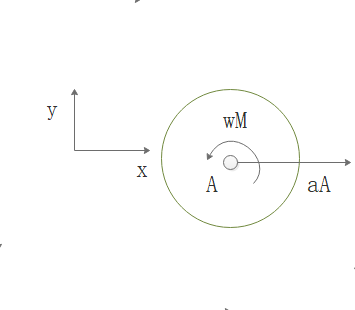
轮子加速度分析
而杆件的加速度分析结果如下：
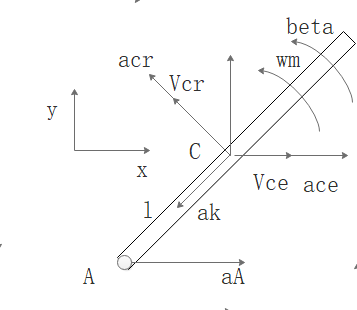
杆加速度分析
根据上面的分析结果列写方程如下：
V c x = V A − ω m l s i n θ V_{cx}=V_A-\omega _m l sin\theta Vcx=VA−ωmlsinθ
− ω m r = V A -\omega _m r =V_A −ωmr=VA
− d ω m d t r = d V A d t -\frac{d\omega _m}{dt} r =\frac{dV_A}{dt} −dtdωmr=dtdVA
1.3动力学分析
根据小车模型受力图进行动力学分析，对轮子列写受力方程如下：
x : − f + F x ′ = M a A x:-f+F_x'=Ma_A x:−f+Fx′=MaA
y : N + F y ′ − M g = 0 y:N+F_y'-Mg=0 y:N+Fy′−Mg=0
对轮子列写力矩方程如下：
对A点:
r为轮子半径。
M M − f r = J M d ω M d t M_M-fr=J_M\frac{d\omega _M}{dt} MM−
最低0.47元/天 解锁文章
扫一扫
1882
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
