LeetCode2322.从树中删除边的最小分数(Java)

原创已于 2025-07-24 23:04:22 修改 · 755 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法

于 2025-07-24 22:59:39 首次发布

LeetCode 专栏收录该内容

6 篇文章

订阅专栏

题目

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的最小分数。

跳转链接：LeetCode2322

前置条件

由于本题涉及到异或值，所以我们需要先掌握有关异或的基本知识：

若已知 A⊕B=C，则：A⊕C=B、B⊕C=A

拓展到本题中来，假设树的总异或值为 s，将树分为三个部分其异或值分别为 s1、s2、s3，则有：

s = s1 ⊕ s2 ⊕ s3

s1 = s ⊕ s2 ⊕ s3

s2 = s ⊕ s1 ⊕ s3

s3 = s ⊕ s1 ⊕ s2

解析

本题要求我们将一个树的两条边删除，使得该树分成三部分，对每个部分求异或值，从而得到三个异或值，取其中最大值和最小值相减得到差 x，要求我们想办法删除两条边从而得到最小的 x。

本题我们可以采用双重DFS，我们先假设树整体为 s，分为三个部分分别为 s1、s2、s3。首先，第一重DFS用于确定一条删除的边，我们从节点 0 开始DFS，进入DFS函数后有子节点 son 和父节点 father，我们将父子节点的边删除，包含子节点的部分记为 s1 而父节点部分由 s2 和 s3 组成。接下来我们要进入第二层DFS，在父节点部分找到一条边划分出 s2 和 s3。

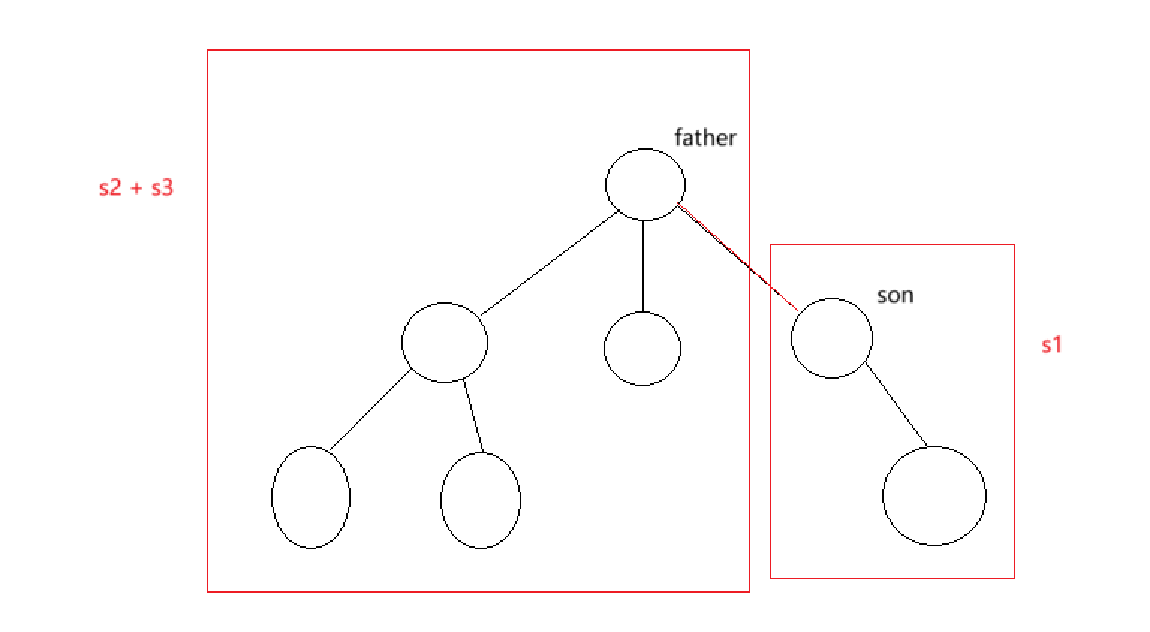
而异或值的求法，我们可以在回溯时将该节点以及其子节点的异或值作为返回值返回，这样我们可以得到 s1 的异或值和 s2 的异或值，而 s3 的异或值我们可以通过 s3 = s ⊕ s1 ⊕ s2 求出(s 可以在最开始时求出)。得到 s1、s2、s3后选出最大值和最小值做差，用 ans 变量来存储最小的差。

public class Solution {
    
    private int s = 0;//整个树的异或值
    private int ans = Integer.MAX_VALUE;
    List<List<Integer>> edge = new ArrayList<>();//edge用于存储点与点之间的边

    public int minimumScore(int[] nums, int[][] edges) {
        int n = nums.length;

        for (int i = 0; i < n; i++) {
            edge.add(new ArrayList<>());
            //计算整个树的异或值
            s ^= nums[i];
        }
        //赋值，edge[i][j] = k表示i和k之间存在边
        for (int[] e : edges) {
            edge.get(e[0]).add(e[1]);
            edge.get(e[1]).add(e[0]);
        }
        //第一次进入DFS，父节点为-1
        dfsSon(0, -1, nums);
        return ans;
    }

    //第一重DFS将树分为s1和s2+s3
    //son为子节点
    //father为父节点
    public int dfsSon(int son, int father, int[] nums){
        int s1 = nums[son];
        //此处进行第一重的DFS，保证每条边都被考虑到
        for (Integer i : edge.get(son)) {
            if(i != father){
                s1 ^= dfsSon(i, son, nums);
            }
        }
        //此处用于进入二重DFS
        for (Integer i : edge.get(son)) {
            if(i == father){
                dfsFather(i, son, s1, son, nums);
            }
        }
        return s1;
    }

    //第二重DFS分割s2和s3
    //s1为s1部分的异或值
    //ack表示s1部分的第一个节点，用于防止s2和s3未分割而计算最小异或差的情况
    public int dfsFather(int son, int father, int s1, int ack, int[] nums){
        int s2 = nums[son];
        //此处用于在s2+s3部分进行分割，DFS保证每条边都被考虑到
        for (Integer i : edge.get(son)) {
            if(i != father){
                s2 ^= dfsFather(i, son, s1, ack, nums);
            }
        }
        //如果father == ack代表s2和s3未分割，因此不能进行求异或差
        if(father != ack){
            ans = Math.min(ans, tackle(s1, s2, s ^ s1 ^ s2));
        }
        return s2;
    }

    //用于计算异或差值
    public int tackle(int s1, int s2, int s3){
        return Math.max(s3, Math.max(s1, s2)) - Math.min(s3, Math.min(s1, s2));
    }

}

留个赞再走吧~