KMP+Z算法（exkmp）（板子）

给萌新们简要介绍一下KMP吧：

KMP：O（m+n）

题：字符串S：abababa  字符串P：ba ,问题：求字符串P在S中出现的次数？

相关延申：给定某个字符串S，再给某个字符串P（len（P）<len（S）），问是否P是S的子串？

然而，学过哈希的大佬们，肯定会用哈希求解，哈希还是比较快的，写过哈希的大佬都知道，哈希有个非常致命的bug，那就是最终求出的哈希值不一定是字符串的哈希值。换句话说，P原本是S的子串，然而哈希可能会求得P不是S的子串。所以，这里给出了KMP的板子以供理解。

因为KMP采用文本的方式讲解的话，那么我实在不容易讲通，我建议读者还是先了解KMP算法的本质后再采用这套板子

KMP模板：

#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int n,m;
int nex[N+1],f[N+1];
//nex数组：最大前缀与最大后缀      f数组：f【i】，以i结尾的后缀所能匹配的长度
char s[N+2],p[N+2];

void kmp(){
	n=strlen(s+1),m=strlen(p+1);
	int j=0;
	nex[1]=0;
//处理nex数组
	for(int i=2;i<=m;i++){
		while(j>0&&p[j+1]!=p[i]) j=nex[j];
		if(p[j+1]==p[i]) j++;
		nex[i]=j;
	}
//处理f数组
	j=0;
	for(int i=1;i<=n;i++){
		while((j==m)||(j>0&&p[j+1]!=s[i])) j=nex[j];
		if(p[j+1]==s[i]) j++;
		f[i]=j;
	}
	for(int i=1;i<=n;i++){
		if(f[i]==m){
			printf("YES");
			return;
		}
	}
	printf("NO");
}

int main(){
	scanf("%s%s",s+1,p+1);
	kmp();
}

其实我们发现，处理nex【】数组和f【】数组的方式是一样的，所以我们也可以采用第二套板子。 （个人推荐kmp的第二套板子）

给道板子题吧：http://oj.daimayuan.top/course/22/problem/908

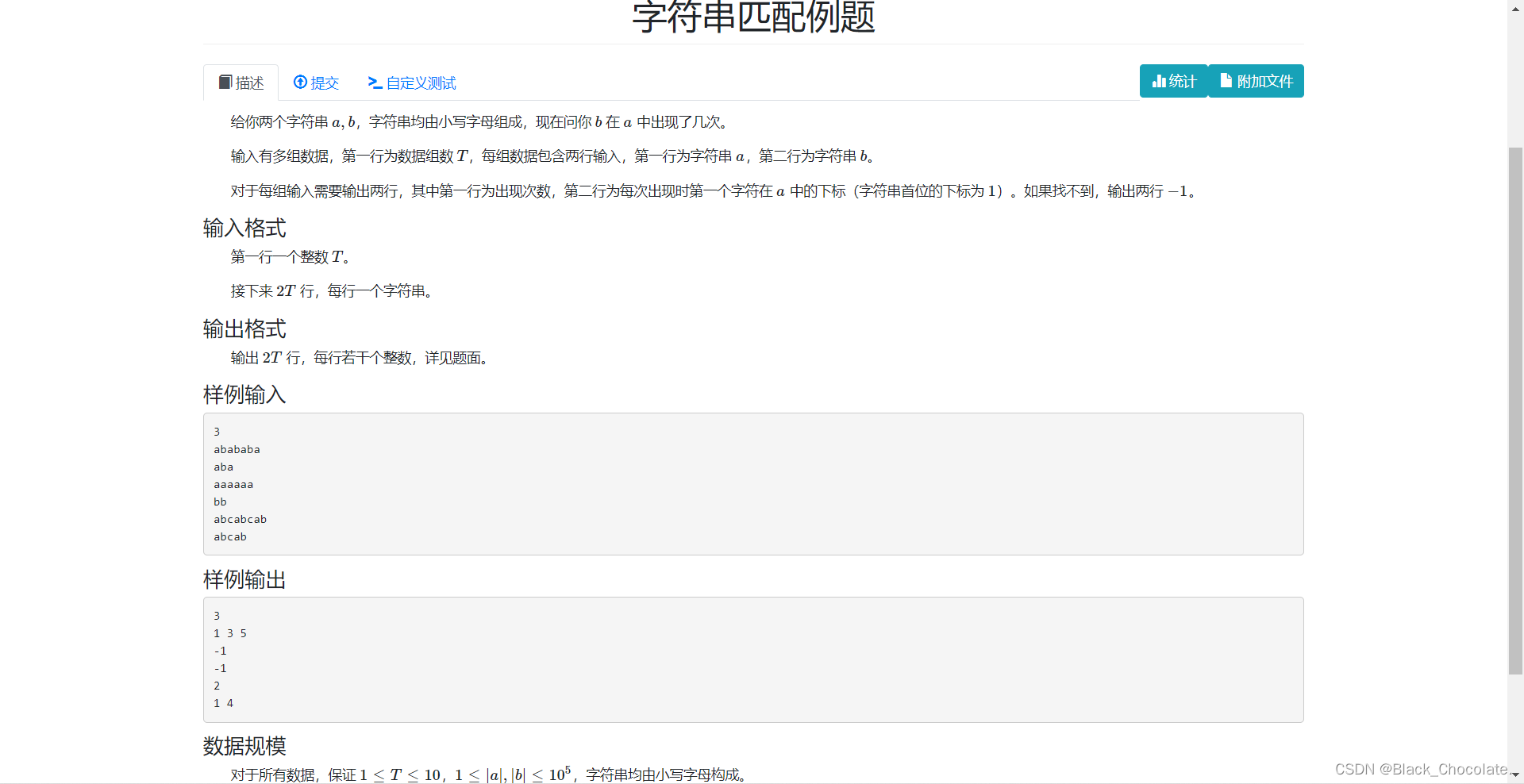
代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int nex[N+1],f[N+1];
char s[N],p[N+1];

inline void kmp(){
	int n=strlen(s+1),m=strlen(p+1);
	p[m+1]='#';
	for(int i=1,j=m+2;i<=n;i++,j++) p[j]=s[i];//将两个字符合并成 p#s 字符串
	int j=0;nex[1]=0;
	for(int i=2;i<=n+m+1;i++){
		while(j&&p[j+1]!=p[i]) j=nex[j];
		if(p[j+1]==p[i]) j++;
		nex[i]=j;
	}
	int ans=0;
	for(int i=m+2;i<=n+m+1;i++)
		if(nex[i]==m) ans++;
	if(!ans) cout<<"-1 -1\n";
	else{
		cout<<ans<<"\n";
		for(int i=m+2;i<=n+m+1;i++)
			if(nex[i]==m) cout<<i-2*m<<" ";
		cout<<"\n";
		
	}
}

int main(){
	 int T;cin>>T;
	 while(T--){
	 	cin>>s+1>>p+1;
	 	kmp();
	 } 
}

这里做一下解释：因为f【】数组记录的是以位置i为后缀的匹配长度。nex【】数组记录的是以i位置结尾的后缀长度（是等于以i位置结束的前缀）。仔细思考就会发现，f【】数组和nex【】数组记录的都是以i位置匹配的字符串长度。所以我们可以将两个字符串进行合并，这样形成一个字符串，f【】数组就可以用nex数组表示（反之也可）。直接判断合并字符串前缀 和 后缀，因为这本来就是f【】数组和nex【】数组的定义。也就相当于在分别在s和p字符串中进行匹配。

这里再介绍一下Z算法。我们习惯把Z算法称为exkmp（扩展kmp算法）

exkmp算法思路是跟kmp算法的思路是一样的。

Z方法：O（n）

唯一不同的就是：

kmp：是以i结束的后缀字符串              exkmp：是以i开始的前缀字符串

这里着重讲一下kmp的next数组，和exkmp的z数组

next数组： KMP算法讲解（next数组求解）_Liu Zhian的博客-优快云博客_kmp next

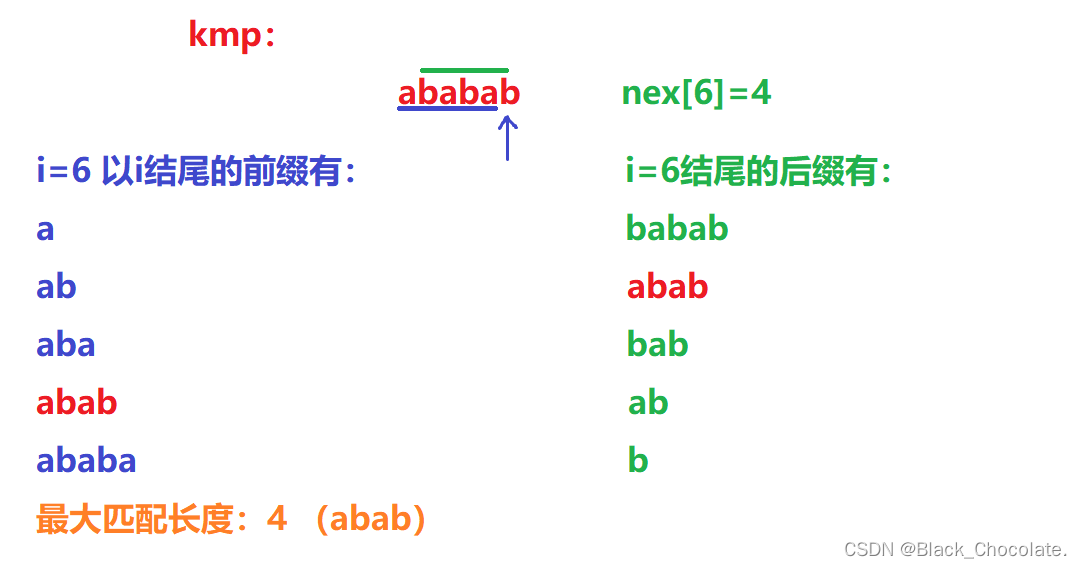
z数组： 

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
char s[N],p[N];
int z[N];//以i为起点所能匹配的长度

inline void exkmp(){
	int n=strlen(s+1),m=strlen(p+1);
	p[m+1]='#';
	for(int i=1,j=m+2;i<=n;i++,j++) p[j]=s[i];
	int L=1,R=0;z[1]=0;
	for(int i=2;i<=n+m+1;i++){
		if(i>R) z[i]=0;
		else{
			int k=i-L+1;
			z[i]=min(z[k],R-i+1);
		}
		while(i+z[i]<=n+m+1&&p[z[i]+1]==p[i+z[i]]) z[i]++;
		if(i+z[i]-1>R) L=i,R=i+z[i]-1;
	}
	int ans=0;
	for(int i=m+2;i<=n+m+1;i++)
		if(z[i]==m) ans++;
	if(!ans) cout<<"-1\n-1\n";
	else{
		cout<<ans<<"\n";
		for(int i=m+2;i<=n+m+1;i++) 
		   if(z[i]==m) cout<<i-m-1<<" ";
	}
	cout<<"\n";	
}

int main(){
	int T;cin>>T;
	while(T--){
		cin>>s+1>>p+1;
	    exkmp();
	}
}

总结：解决字符串匹配的问题，kmp和exkmp都适用，他们的时间复杂度可以近似O（n），所以可以任意选择。

再补个结论吧：一个循环字符串的最小覆盖字符串长度为：n-nex[n]