BST的查找

已于 2024-05-06 15:25:14 修改
阅读量257 收藏 4
点赞数 11
分类专栏： 小浩算法cpp题解 文章标签： 算法 数据结构 图论
于 2024-05-06 15:21:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Youweretrouble/article/details/138495883
版权
本文介绍了作者使用迭代和递归方法在二叉查找树(BST)中搜索特定元素的过程，以及相关的树结构操作如深度计算、中序遍历和验证BST性质。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

前言

BST（Binary Search Tree）二叉查找树也太简单了吧，今天做的这个有点简单哈哈哈哈。

我的思路

迭代

迭代就是我的主要工作在于更新变量上了，如果我想要找的值比根节点小，我就用根节点的左孩子去替代当前的值。用while循环去控制不为空的条件。

node* search_BST(node* root,char str) {
	while (root != nullptr) {
		if (root->info == str) {
			return root;
		}
		else if(root->info <str) {
			root = root->right;
		}
		else if (root->info > str) {
			root = root->left;
		}
	}
	cout << "此BST中没有这个元素！" << endl;
	return NULL;
}

递归

递归就是我直接调用自己去找，把我的子树当参数去传递给这个函数。我还是喜欢迭代一点。

	node* search_BST_recursion(node* root, char str) {
		if (root == nullptr) {
			cout << "此BST中没有这个元素！" << endl;
			return NULL;
		}
		else if (root->info == str) {
			return root;
		}
		else if(root->info < str) {
			search_BST_recursion(root->right, str);
		}
		else {
			search_BST_recursion(root->left, str);
		}
	}
};

我还考虑了一下深拷贝和浅拷贝的问题，一般来说，我们用指针去返回一个对象那基本就是深拷贝了呵呵。

结果

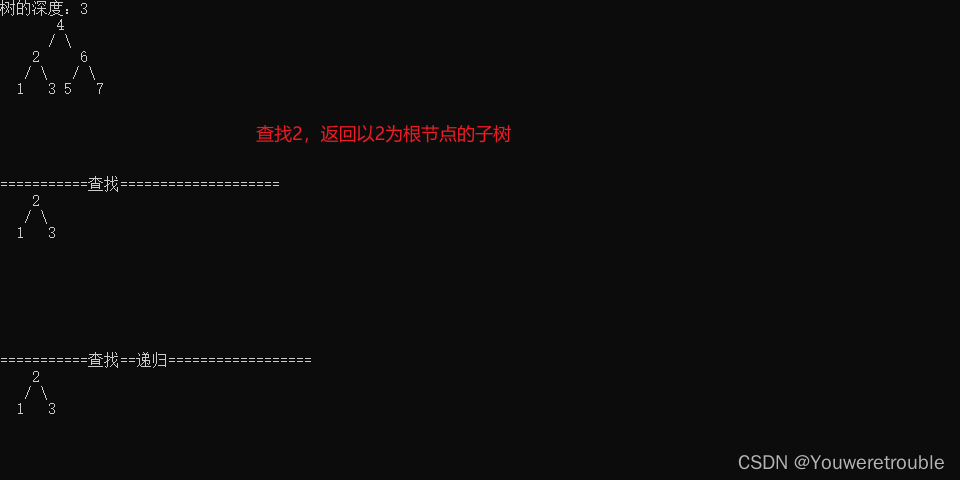
在这里插入图片描述
在这里插入图片描述

我的代码

#include <iostream>
#include<algorithm>
#include<cmath>
#include <queue> 
#include<climits>
using namespace std;

struct node {
	char info;
	node* left;
	node* right;
	node(char data) :info(data), left(nullptr), right(nullptr) {

	};
	node() :info(NULL), left(nullptr), right(nullptr) {

	};
};

class binaryTree {
private:
	node* root;
public:
	binaryTree() {
		root = new node(NULL);
	}

	//得到树的根结点
	node* getRoot() {
		return root;
	}
	//得到树的根结点
	void setRoot(node* newRoot) {
		 root=newRoot;
	}

	//以递归的方式构建一棵树
	void createTree(node*& t,string data,int &i) {
		char str=data[i];
		/*cin >> str;*/
		if (str == '#') {
			t = NULL;
		}
		else {
			t = new node;//为t开辟空间
			t->info = str;
			createTree(t->left,data,++i);
			createTree(t->right,data,++i);
		}
	}

	//树的深度
	int depth(node* root) {
		if (root == nullptr) {
			return 0;
		}
		int left = depth(root->left);
		int right = depth(root->right);
		return max(left, right) + 1;
	}

	//打印一棵树满二叉树，只能打印满二叉树，节点数目最好不要超过10
	void print(node*& root) {
		//存放打印的二叉树
		char str[10][100] = {};
		queue<node*> q;
		int h = depth(root);
		q.push(root);
		int index = 0;
		while (!q.empty()) {
			int size = q.size();
			//存放每一层的节点
			vector<char> list;
			for (int i = 0; i < size; i++) {
				node* temp = q.front();
				q.pop();
				list.push_back(temp->info);
				//cout << temp->info;
				if (temp->left != nullptr) {
					q.push(temp->left);
				}
				if (temp->right != nullptr) {
					q.push(temp->right);
				}
			}
			bool flag = true;
			int j = 0;
			//打印前面部分空白
			while (j <= 2 * h - 1 - index) {
				str[index][j] = ' ';
				j++;

			}
			//保持第一行居中
			if (index == 0) {
				for (int m = 0; m < h - 2; m++) {
					str[index][j++] = ' ';
				}
			}

			for (int k = 0; k < list.size(); k++) {
				//如果是一层最后一个节点
				if (k == list.size() - 1) {
					str[index][j++] = list[k];
				}
				else {
					//相邻左右子节点
					if (k % 2 == 0) {
						str[index][j++] = list[k];
						for (int l = 0; l < 3 + 2 * (h - index / 2 - 1); l++) {
							str[index][j++] = ' ';
						}
					}
					else {
						str[index][j++] = list[k];
						str[index][j++] = ' ';
					}
				}
			}

			index += 2;
			//cout << endl;
		}
		for (int i = 0; i < 10; i++) {
			if (i % 2 == 1) {
				for (int j = 0; j < 100; j++) {
					str[i][j] = ' ';
				}
			}
		}
		for (int i = 0; i < 10; i++) {
			if (i % 2 == 0) {
				for (int j = 0; j < 100; j++) {
					if (str[i][j] - '0' >= 0 && str[i][j] - '0' <= 9 && i < 2 * h - 2) {
						str[i + 1][j - 1] = '/';
						str[i + 1][j + 1] = '\\';
					}

				}
			}
		}
		for (int i = 0; i < 10; i++) {
			for (int j = 0; j < 100; j++) {
				cout << str[i][j];
			}
			cout << endl;
		}
	}

	void DeepFirstSearch(node* root) {
		if (root == NULL) {
			return;
		}
		else {
			cout << root->info << ' ';
			DeepFirstSearch(root->left);
			DeepFirstSearch(root->right);
		}

	}

	void BreadthFirstSearch(node* root) {
		queue<node> myTree;
		if (root != nullptr) {
			myTree.push(*root);
		}
		while (!myTree.empty()) {
			cout << myTree.front().info << ' ';
			if (myTree.front().left != nullptr) {
				myTree.push(*(myTree.front().left));
			}
			if (myTree.front().right != nullptr) {
				myTree.push(*(myTree.front().right));
			}
			myTree.pop();
		}
	}

	//用于BFS递归的主函数
	void BFS_Recursion(node* root, int level, vector<vector<char>>& res) {
		if (root == nullptr) {
			return;
		}
		if (res.size() < level) {
			res.push_back(vector<char>());
		}
		res[level - 1].push_back(root->info);
		BFS_Recursion(root->left, level + 1, res);
		BFS_Recursion(root->right, level + 1, res);
	}

	void BreadthFirstSearch_recursion(node* root) {
		vector<vector<char>> res;
		BFS_Recursion(root, 1, res);
		for (int i = 0; i < res.size(); i++) {
			for (int j = 0; j < res[i].size(); j++) {
				cout << res[i][j] << " ";
			}
		}
	}

	//验证是否为二叉搜索树
	void isBST(node* root) {
		//先创建一个数组
		vector<char> midOrderArr;
		midOrder(root, midOrderArr);
		//输出看一下我的数组里面存的是不是中序遍历的值
		for (int i = 0; i < midOrderArr.size(); i++) {
			cout << midOrderArr[i] << ' ';
		}
		cout << endl;
		for (int i = 0; i < midOrderArr.size() - 1; i++) {
			if (midOrderArr[i] >= midOrderArr[i + 1]) {
				cout << "该二叉树 不是一颗二叉搜索树！" << endl;
				return;
			}
		}
		cout << "该二叉树 是一颗二叉搜索树！" << endl;
	}

	//二叉树的中序遍历
	void midOrder(node* root, vector<char>& Arr) {
		if (root == nullptr) {
			return;
		}
		midOrder(root->left, Arr);
		Arr.push_back(root->info);
		midOrder(root->right, Arr);
	}

	bool isBST_Recursion(node* root, long long min, long long max) {
		if (root == nullptr) {
			return true;
		}
		if (root->info <= min || root->info >= max) {
			//cout << "该二叉树不是一个二叉搜索树";
			return false;
		}
		return isBST_Recursion(root->left, min, root->info) && isBST_Recursion(root->right, root->info, max);
	}

	node* search_BST(node* root,char str) {
		while (root != nullptr) {
			if (root->info == str) {
				return root;
			}
			else if(root->info <str) {
				root = root->right;
			}
			else if (root->info > str) {
				root = root->left;
			}
		}
		cout << "此BST中没有这个元素！" << endl;
		return NULL;

	}

	node* search_BST_recursion(node* root, char str) {
		if (root == nullptr) {
			cout << "此BST中没有这个元素！" << endl;
			return NULL;
		}
		else if (root->info == str) {
			return root;
		}
		else if(root->info < str) {
			search_BST_recursion(root->right, str);
		}
		else {
			search_BST_recursion(root->left, str);
		}
	}
};

int main() {
	binaryTree T;
	node* root = T.getRoot();
	string data = "421##3##65##7##";
	string data2 = "1248##9##5##36##7##";
	char str = '2';
	int i = 0;
	T.createTree(root,data,i);
	cout << "树的深度：" << T.depth(root) << endl;
	T.print(root);
	cout << "===========查找====================" << endl;
	binaryTree resTree;
	if (T.search_BST(root, str)) {
		resTree.setRoot(T.search_BST(root, str));
		node* resTreeRoot = resTree.getRoot();
		resTree.print(resTreeRoot);
	}
	cout << "===========查找==递归==================" << endl;
	binaryTree resTree2;
	if (T.search_BST_recursion(root, str)) {
		resTree2.setRoot(T.search_BST_recursion(root, str));
		node* resTreeRoot2 = resTree2.getRoot();
		resTree.print(resTreeRoot2);
	}
	return 0;
}
c#bst查找
weixin_43919162的博客
12-13 387
using System; using 所以; using System.Collections.Generic; //想用list必须有他！！！ /*1． 设计BST 的左右链存储结构，并实现BST插入（建立）、删除、查找和排序算法。 2． 实现折半查找算法。 3． 实验比较：设计并产生实验测试数据，考察比较两种查找方法的时间性能，并与理论结果进行比较。以下具体做法可作为参考： （1） 第1组测...
哈工大数据结构作业四——BST查找结构和折半查找的实现与比较
weixin_45406155的博客
11-06 3239
哈工大数据结构实验三——图形结构及其应用 哈工大课程实验合集 1.实验要求 步骤 2.实验步骤 2.1 设计BST 先看看BST树是啥。 BST也叫二叉查找树，它本质上也是一棵二叉树。只不过对于二叉树的每个节点来说，节点存储的值大于所有的左子树的节点存储的值，小于所有的右子树的节点存储的值。 有了这个性质，我们利用BST进行查找就很简单，只需要将要查找的值和当前节点存储的值进行比较，等于就查找到，大于这个节点存储的值就往右子树走，否则就往左走，一直走到空节点为止。(可以看到，和折半查找非常类似，但是却比折半
二叉查找树（BST）
DaisyMaria的博客
09-08 1084
关于二叉查找树（BST）的一些问题
二叉查找树（BST）和折半查找（C语言实现）
qq_62225979的博客
11-14 1662
二叉查找树（BST）的实现，以及和折半查找的性能比较。数据结构作业（C语言实现）
BST的查找、插入、删除
JTY541464341的博客
03-30 879
BST的查找、插入、删除 BST (binary search tree) 二叉搜索树 结合了vector和list的优点 主要接口有三种：查找，插入，删除 查找： 时间复杂度O(h)（即不超过树的高度） 由于BST在局部具有顺序性、在整体具有单调性的特点，因此BST的直接投影与其中序遍历相符合。关键码从左到右依次单调递增。 在查找目标关键码时，动作类似于vector中的二分查找。因为BST的...
数据结构 查找结构与排序方法
qq_62585151的博客
11-15 506
BST 查找结构与折半查找方法的实现与实验比较要求编写程序实现 BST 存储结构的建立（插入）、删除、查找和排序算法；实现折半查找算法；比较 BST 查找与折半查找方法的时间性能。
二叉排序树（BST）查找算法详解之C语言版
sunnyoldboy博客
10-04 3898
在二叉排序树上查找某个结点，其实就是遍历二叉树。由于二叉排序树上的结点是有序的，因此不需要使用普通二叉树的遍历算法，其有自己一套简单的遍历算法，即从树根开始进行遍历，如果待查找元素小于树根元素，则向左遍历，否则向右遍历，如果相等结束遍历。
二叉排序树（BST查找、插入、删除、遍历）——基于树的查找（一）
热门推荐
weixin_39651041的博客
04-21 1万+
二叉排序树 二叉排序树（Binary Search Tree，BST）：又称二叉查找树，是一种高效的数据结构。 定义 二叉排序树或者是一棵空树，或者是具有如下特性的二叉树： 若左子树不空，则左子树上所有结点的值均小于或等于根结点的值； 若右子树不空，则右子树上所有结点的值均大于或等于根结点的值； 左、右子树也分别为二叉排序树 如下便是一棵二叉排序树 根据定义，再根据二叉树中...
《数据结构与算法》实验：查找结构的实验比较——二叉查找树BST & 二分（折半）查找
Zhuoning Guo's Blog
02-02 4641
《数据结构与算法》实验和课程Github资源 《数据结构与算法》实验：线性结构及其应用——算术表达式求值 《数据结构与算法》实验：树型结构的建立与遍历 《数据结构与算法》实验：图结构的建立与搜索 《数据结构与算法》实验：查找结构的实验比较——二叉查找树BST & 二分（折半）查找 《数据结构与算法》实验：排序算法实验比较——选择排序 & 堆排序 《数据结...
[Java DS] 搜索树(BST)的查找、插入、删除 (学习总结）
weixin_61567666的博客
03-18 1382
1.BST： 满足如下规则的二叉树： 树中的任意结点，结点的值（就是我们的key），满足一定 大于 它的左子树的所有值；小于 它的右子树的所有值。 这些存在于二叉树结点中的这些值，就是我们搜索场景下的key 注意：BST 的 key 不允许重复 2.contains 查找 k 是否存在于该集合（BST）中，首先从根开始查找。 k == root.key：找到了，存在。k < root.key ：一定在根的左子树中去查找。反之同理。 遇到null 说明要找的key 不在集合中。 3.删除
Python实现二叉搜索树BST的方法示例
01-20
二叉排序树（BST）又称二叉查找树、二叉搜索树 二叉排序树(Binary Sort Tree)又称二叉查找树。它或者是一棵空树；或者是具有下列性质的二叉树： 1.若左子树不空，则左子树上所有结点的值均小于根结点的值； 2.若...
BST 存储结构的建立（插入）、删除、查找和排序，实现折半查找C语言代码
04-07
1．BST 的左右链存储结构，并实现 BST 插入（建立）、删除、查找和排序算法 2． 折半查找的递归和非递归算法 3． (1) 第 1 组测试数据： n=1024 个已排序的整数序列（如 0 至 2048 之间的奇数）；第 2 组测试数据：...
"BST查找结构与折半查找算法实验比较
实验目的是通过实际操作和比较分析，掌握BST的基本操作，并比较BST查找结构与折半查找方法的时间性能，培养学生的数据结构设计和程序设计能力。 首先，本实验要求设计BST的左右链存储结构，并实现插入、删除、查找...
"数据结构与算法课程实验报告：BST查找结构与折半查找方法的比较实验
实验41报告：BST查找结构与折半查找方法的实现与实验比较 哈尔滨工业大学计算机科学与技术学院 课程名称：数据结构与算法 课程类型：必修 班级：1703002 学号：1170500913 姓名：熊健羽 实验日期：2018.12.20 成绩...
快速排序优化技巧详解：提升性能的关键策略
最新发布
qq_43947876的博客
06-12 447
快速排序是高效排序算法，但原始实现存在性能瓶颈。本文探讨五种优化策略：1）随机选择基准，避免有序数组的最坏情况；2）三数取中法，选取更均衡的基准；3）小数组切换插入排序，减少递归开销；4）尾递归优化，降低栈溢出风险；5）双轴快排（如Java Arrays.sort()），通过双基准提升分区效率。每种方法附Java代码示例，显著提升算法性能，适用于实际开发场景。优化后，快速排序的时间复杂度更趋近理想O(n log n)，空间效率更高。
【DRL】最简单的策略梯度(Policy Gradient)算法
xfxuezhang.cn
06-12 99
最简策略梯度(Policy Gradient)算法的实现
【LeetCode 热题100】网格路径类 DP 系列题：不同路径 & 最小路径和（力扣62 / 64 ）（Go语言版）
小韩的博客
06-08 593
本篇介绍了网格路径类动态规划问题，涵盖 LeetCode 第 62 题“不同路径”和第 64 题“最小路径和”。通过定义状态 `dp[i][j]` 和转移方程，分别解决路径计数与最小代价问题。两题均支持一维数组优化空间复杂度。总结对比了两题的异同，并延伸至带障碍路径、三角形路径等问题，帮助读者掌握网格 DP 的核心思路：明确状态、写出转移、找准边界。
【算法笔记】树套树
fans2306的博客
06-08 1060
在面对二维区间统计问题查询某个一维区间中，大于某个值的数的个数对一个序列同时支持区间查询 + 单点修改我们常用的一维数据结构（如线段树、树状数组）往往显得力不从心。树套树。“树套树”顾名思义，就是一棵树中的每个节点再套一棵树。外层：线段树/树状数组，按照下标维护区间内层：平衡树（如 STLmultiset或手写）维护该区间内的值集合单点修改某个值查询区间中小于/大于某值的数的个数查询区间第kkk小数值（需平衡树）
【2025CVPR】模型融合新范式：PLeaS算法详解（基于排列与最小二乘的模型合并技术）
hasakie的博客
06-08 134
本文深入解析ICLR 2025顶会论文《PLeaS: Merging Models with Permutations and Least Squares》，揭示模型融合领域突破性进展.随着开源模型的爆发式增长，如何高效合并多个专用模型成为关键挑战。传统方法存在三大痛点：而PLeaS创新性地解决了这些难题，实现：PLeaS（Permutations and Least Squares）包含两个核心阶段： 数学本质​： minPi​∈Sdi​​​∥ZiA​−Pi​ZiB​∥F2​ 其中ZiA​,ZiB​是
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值