最长递增子序列详解 CPP

Youweretrouble

于 2024-05-10 10:47:59 发布

阅读量894

点赞数 16

分类专栏：小浩算法cpp题解文章标签：算法数据结构动态规划

本文链接：https://blog.youkuaiyun.com/Youweretrouble/article/details/138603421

版权

前言

今天继续做动态dp的第三题，最大子序和，昨天做最大连续子数组的和已经有一些写状态转移方程的经验了，今天自己想了一个思路一。

思路梳理

题解最优思路

写到这里我想惊叹一下数学语言的魅力，因为我虽然想清楚了但是却表达不清楚。一个数学公式代替了我的一大坨废话。
在这里插入图片描述

在这里插入图片描述
这里最大的坑在于，状态转移的前一个状态需要满足两个条件。从我自己的思路三优化到这里也并不复杂，感觉我自己的思路就好像是先把水煮开再一起下饺子，官方思路是冷水的时候我就可以把饺子放下去慢慢煮了。很多判断可以在遍历的时候就做了。
以下是代码：

int max_subArr_Ascending_order_optimize_Original(vector<int> Arr) {
   
    vector<int> resArr(Arr.size());
    for (int i = 0; i < Arr.size(); i++) {
   
        //先把最差的情况确定好，最差的情况也不过就是1了
        resArr[i] = 1;
        //然后再循环左边比它小的最大值
        for (int j = 0; j < i; j++) {
   
            if (Arr[j] < Arr[i]) {
   
                resArr[i] = max(resArr[j] + 1, resArr[i]);
            }
        }
    }
    return *max_element(resArr.begin(),resArr.end());
}

我的思路

思路一考虑连续对一半 ×

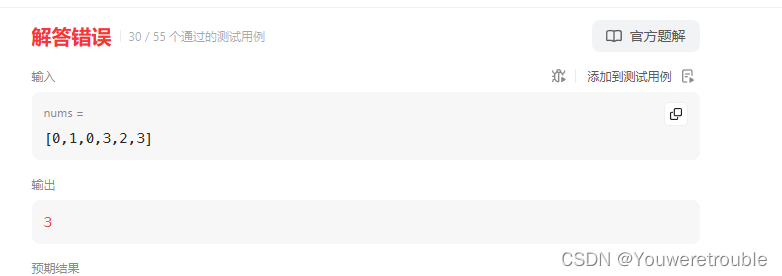
跟昨天的类似，也是以子数组的最后一个元素的位置作为标记。首先我找到最大的连续升数组，然后再在这个基础上加上前面的不连续的。但是很遗憾，这个思路只通过了一半的测试用例，想想看确实是有很大问题的。不应该考虑连续，连续的bug太大了。
在这里插入图片描述

class Solution {
   
public:
    int lengthOfLIS(vector<int>& Arr) {
   
        int res = 1;
        vector<int> resArr(Arr.size());
        resArr[0] = 1;
        int left_max_location;
        for (int i = 1; i < Arr.size(); i++) {
   
            // 首先找到左边比它小，且最大的元素
            left_max_location = search_left_less_than(i, Arr, resArr);
            if (left_max_location == -1) {
   
                resArr[i] = 1;
            } else {
   
                resArr[i] = left_max_location + 1;
            }
            if (resArr[