65. 有效数字【状态机】

65. 有效数字

65. 有效数字

给定一个字符串s，返回s是否是一个 有效数字。

例如，下面的都是有效数字："2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"，而接下来的不是："abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"。

一般的，一个 有效数字 可以用以下的规则之一定义：

1. 一个 整数 后面跟着一个 可选指数。
2. 一个 十进制数 后面跟着一个 可选指数。

一个 整数 定义为一个 可选符号 '-' 或 '+' 后面跟着 数字。

一个 十进制数 定义为一个 可选符号 '-' 或 '+' 后面跟着下述规则：

1. 数字 后跟着一个 小数点 .。
2. 数字 后跟着一个 小数点 . 再跟着 数位。
3. 一个 小数点 . 后跟着 数位。

指数 定义为指数符号 'e' 或 'E'，后面跟着一个 整数。

数字 定义为一个或多个数位。

示例 1：

输入：s = "0"

输出：true

示例 2：

输入：s = "e"

输出：false

示例 3：

输入：s = "."

输出：false

提示：

• 1 <= s.length <= 20
• s 仅含英文字母（大写和小写），数字（0-9），加号 ‘+’ ，减号 ‘-’ ，或者点 ‘.’ 。

解题思路

状态机：

1. 状态机是用于描述对象在生命周期内可能的状态
2. 以及特定事件触发的状态转移

比如用Chat-GPT搜索问题时，用户可感知到的简要状态机如下

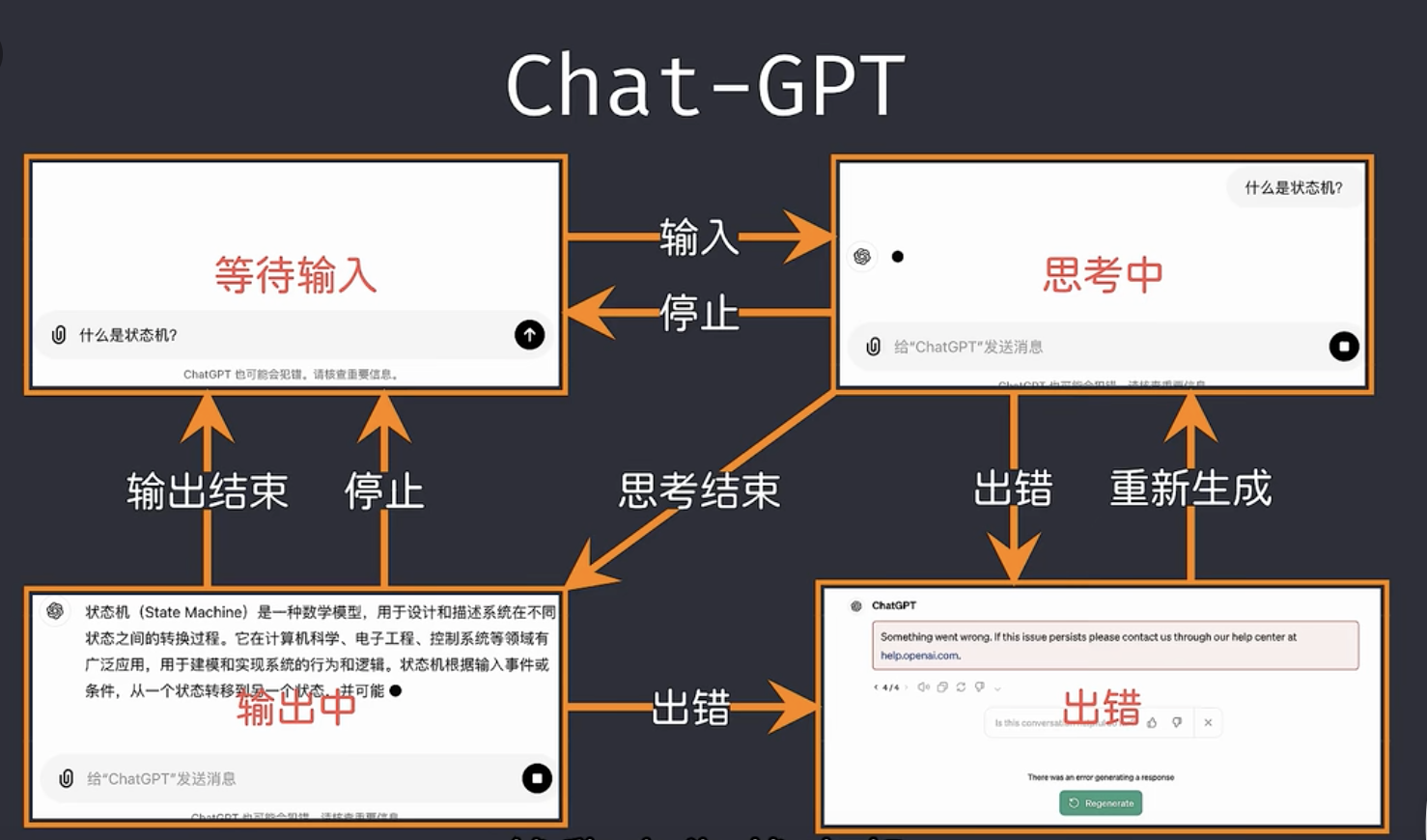
综上：状态机就是解决某一个业务逻辑中，会有多个不同的状态，他们会因为不同的事件导致状态变更。

初态+事件 --> 次态【还可能伴随其他动作】

本题中一共会有如下十个状态，图中圆圈表示：

1. 开始态Start
2. 符号态Sign:如 +1.2中的+
3. 整数态Int：如2
4. 无前导数字的小数点态Dot：如 .1中的.
5. 有前导数字的小数点态Int_Dot：如1.中的.
6. 小数态Dec：如1.1
7. 科学计数法态E：如2e10中的e
8. 科学计数法部分的符号态E_Sign:如2e-2中的-
9. 科学计数法的数字态E_Num：如2e3中的3
10. 非法态Invalid：表示不是一个有效数字了，非法态太多，图中未画出

事件则是遇到的下个字符，共有五种可能，下图顶部以及转移图中的带颜色箭头：

1. 遇到符号
2. 遇到数字
3. 遇到小数点
4. 遇到指数复合E或e
5. 遇到其他字符：注意，遇到其他字符会进入非法态，非法态太多，图中未画出

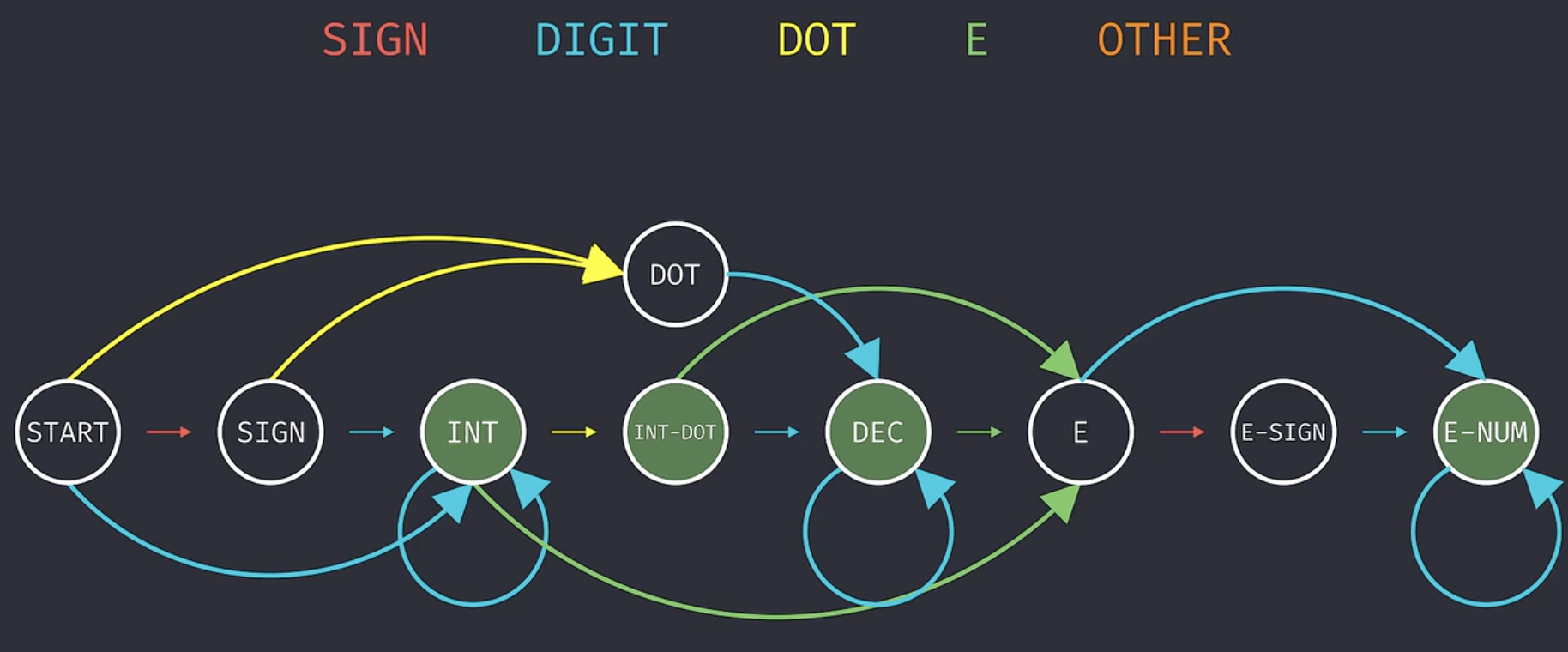
所以本题，我们就是要将状态以及状态转移图定义出来，然后遍历输入的字符串，进入非法态时，说明不会是有效数字了，反之，如果所有字符都遍历完成,处于合法状态，说明输入的字符串是一个有效数字。

注：最终的合法状态只有四个：INT，INT_DOT，DEC，E_NUM

如：“-3.14e2”，我们对照上图走一遍状态转移，从头遍历字符串的每个字符

• 从Start态开始遇到-，进入符号态Sign
• 遇到3，进入数字态Int
• 遇到.，进入有前导数字的小数态Int_Dot
• 遇到1，进入小数态Dec
• 遇到4，仍然是小数态Dec
• 遇到e，进入指数态E
• 遇到2，进入指数数字态E_Num

遍历完字符串"-3.14e2"后，最终停留在了指数数字态E-Num，是一个合法状态，所以字符串"-3.14e2"是一个有效数字

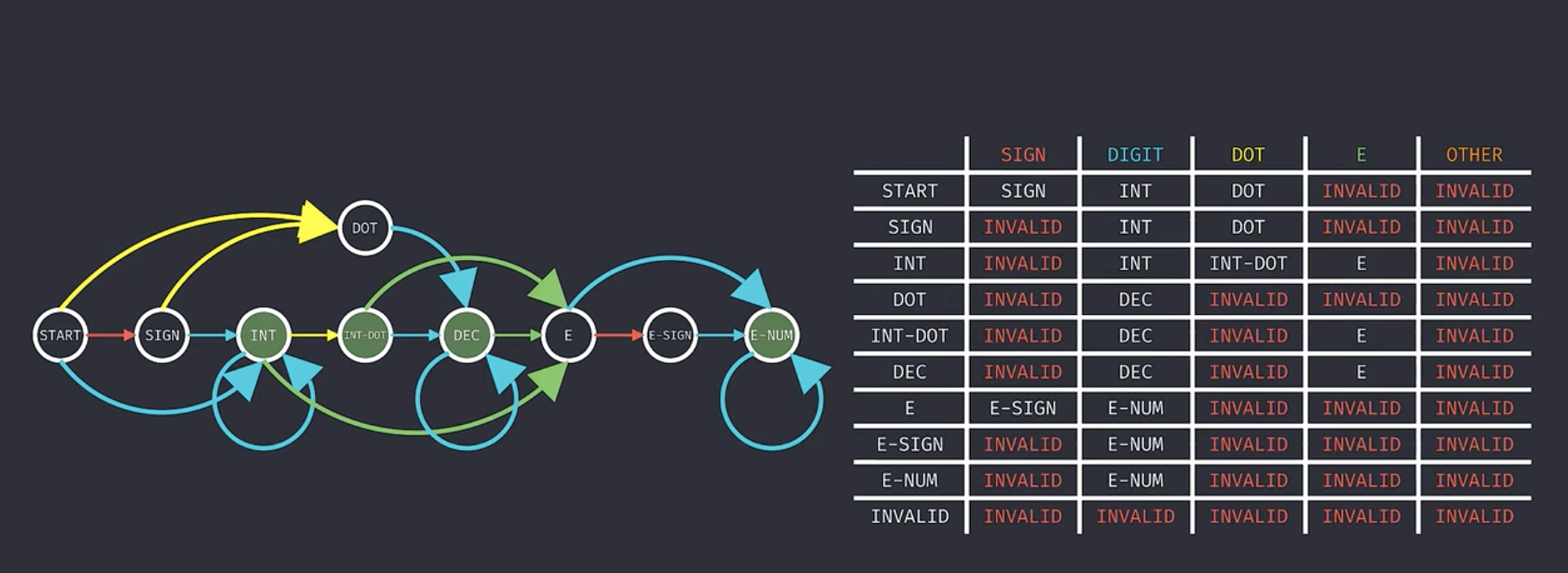
正式进入编码时，我们可以首先根据状态转移图初始化二维数组表示，如下

i行表示当前所处状态(当前初态），j表示当前状态遇到了何种事件，（i，j）位置的值便是初态+事件-->次态【这里没有做其他动作，就是变为次态】】，工作中用map保存状态转移图更常见一些，所以本题我也是用了map，而不是二维数组，但也可以先填充好二维数组，然后对照着二维数组定义好map，这样可以做到不重不漏。

Go代码

type State int
type Event int

// 定义十个状态
const (
    State_START State = iota
    State_SIGN
    State_INT
    State_DOT
    State_INT_DOT
    State_DEC
    State_E
    State_E_SIGN
    State_E_NUM
    State_INVAILD
)

// 定义五个事件
const (
    Event_SIGN Event = iota
    Event_DIGIT
    Event_DOT
    Event_E
    Event_OTHER
)

func isNumber(s string) bool {
    // 定义状态转移图,map中找不到的就是非法态
    transfer := map[State]map[Event]State{
        // 初始态，遇到各种事件后变为何种次态
        State_START:map[Event]State{
            Event_SIGN:State_SIGN,
            Event_DIGIT:State_INT,
            Event_DOT:State_DOT,
        },
        // 符号态，遇到各种事件后变为何种次态
        State_SIGN:map[Event]State{
            Event_DIGIT:State_INT,
            Event_DOT:State_DOT,
        },
        // 数字态，遇到各种事件后变为何种次态
        State_INT:map[Event]State{
            Event_DIGIT:State_INT,
            Event_DOT:State_INT_DOT,
            Event_E:State_E,
        },
        // 无前导数字小数点态，遇到各种事件后变为何种次态
        State_DOT:map[Event]State{
            Event_DIGIT:State_DEC,
        },
        // 有前导数字小数点态，遇到各种事件后变为何种次态
        State_INT_DOT:map[Event]State{
            Event_DIGIT:State_DEC,
            Event_E:State_E,
        },
        // 小数态，遇到各种事件后变为何种次态
        State_DEC:map[Event]State{
            Event_DIGIT:State_DEC,
            Event_E:State_E,
        },
        // 指数态，遇到各种事件后变为何种次态
        State_E:map[Event]State{
            Event_SIGN:State_E_SIGN,
            Event_DIGIT:State_E_NUM,
        },
        // 指数符号态，遇到各种事件后变为何种次态
        State_E_SIGN:map[Event]State{
            Event_DIGIT:State_E_NUM,
        },
        // 指数数字态（题目说了指数的数字部分会是整数，故不用考虑小数态了），遇到各种事件后变为何种次态
        State_E_NUM:map[Event]State{
            Event_DIGIT:State_E_NUM,
        },
    }
    
    // 初始态开始，遍历每个字符，看看能够最终还是有效态
    state := State_START
    for i := 0;i < len(s);i++{
        event := getEvent(s[i])
        if _ ,ok := transfer[state][event];!ok {
            return false
        }
        state = transfer[state][event]
    }

    // 字符串遍历结束后，最终是否处于一个合法状态
    return state == State_INT || state == State_INT_DOT || state == State_DEC || state == State_E_NUM 
}

func getEvent(c byte) Event {
    switch c {
        case '0', '1', '2', '3', '4', '5', '6', '7', '8', '9':
            return Event_DIGIT
        case 'e','E':
            return Event_E
        case '.':
            return Event_DOT
        case '+','-':
            return Event_SIGN
        default :
            return Event_OTHER
    }
}