98. 验证二叉搜索树【二叉树】

98. 验证二叉搜索树

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

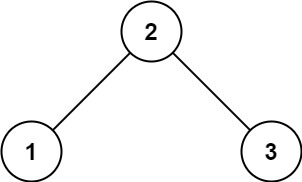
输入：root = [2,1,3]
输出：true

示例 2：

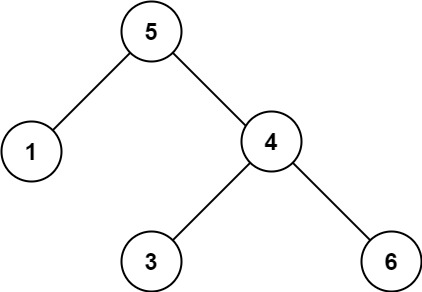
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在$[1,10^4]$ 内
• $-2^{31}<=Node.val<=2^{31}-1$

解题思路

一：中序遍历二叉树用切片保存，遍历完成后，判断切片是否是完全递增的，是的话就是二叉搜索树
二：中序遍历的时候，记录前一个节点，直接比较是否递增
三：递归左右节点的值是否在符合条件的范围内

1. 代码略
2. 代码如下

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidBST(root *TreeNode) bool {
    
    if root == nil {
        return true
    }
    curTreeNode := root
    var preTreeNode *TreeNode // 记录前一个节点
    stack := make([]*TreeNode,0)

    for curTreeNode != nil || len(stack) != 0 {
        if curTreeNode != nil {
            stack = append(stack,curTreeNode)
            curTreeNode = curTreeNode.Left  // 左
        } else {
            curTreeNode = stack[len(stack)-1]  // 中
            stack = stack[0:len(stack) - 1]
            // 二叉搜索树的中序遍历会严格递增，不符合时可以直接返回false
            if preTreeNode != nil && curTreeNode.Val <= preTreeNode.Val {
                return false
            }
            preTreeNode = curTreeNode // 记录前一个访问的节点
            curTreeNode = curTreeNode.Right // 右
        }
    }

    return true

}

3. 代码如下

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidBST(root *TreeNode) bool {
    /*乍一看，这是一个平凡的问题。只需要遍历整棵树，检查 node.right.val > node.val 和
    node.left.val < node.val 对每个结点是否成立。
    问题是，这种方法并不总是正确。不仅右子结点要大于该节点，整个右子树的元素都应该大于该节点
    这意味着我们需要在遍历树的同时保留结点的上界与下界，判断该结点的值是否在范围内。*/
    if root == nil {
        return true
    }
    
    //最初根节点的值在int范围内即可
    return dfs(root,math.MinInt64,math.MaxInt64)

}

func dfs(root *TreeNode,min,max int64) bool {
    if root == nil {
        return true
    }
    if int64(root.Val) < min || int64(root.Val) > max {
        return false
    }
    
    //由于root.Val的值可以一开始就是int的边界，故-1和+1可能会越界，因此转成int64型
    left := dfs(root.Left,min,int64(root.Val) - 1) // 左子树取数范围
    right := dfs(root.Right,int64(root.Val) + 1,max) // 右子树取数范围
    return left && right
}