404. 左叶子之和

404. 左叶子之和

404. 左叶子之和

给定二叉树的根节点 root，返回所有左叶子之和。

示例 1：

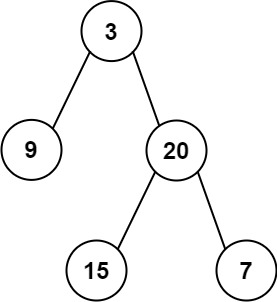
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

思路

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。

因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

大家思考一下如下图中二叉树，左叶子之和究竟是多少？

其实是0，因为这棵树根本没有左叶子！

那么判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下：

if root.Left != nil  && root.Left.Left == nil && root.Left.Right == nil {
    左叶子节点处理逻辑
}

递归法

递归的遍历顺序为前序遍历（中左右），是因为遍历到符合条件的节点时可以立马累加到左叶子数值之和的结果上。

递归三部曲：

1. 确定递归函数的参数和返回值
   判断一个树的左叶子节点之和，那么一定要传入树的根节点，在遍历的过程中就不断累计符合条件的数据，故有一个参数res

func dfs(root *TreeNode,res *int) {}

2. 确定终止条件
   如果遍历到空节点，那么左叶子值一定是0

if root == nil {
        return 
    }

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：

if root == nil {
     return 
 }
 // 叶子节点没有左孩子，可以直接返回了
 //其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层罢了
 if root.Left == nil && root.Right == nil {
     return 
 }

3. 确定单层递归的逻辑
   当遇到左叶子节点的时候，记录数值，然后继续从左右子树中找符合条件的节点。

Go代码如下：

// 要找的是父节点的左孩子，并且是叶子节点
if root.Left != nil  && root.Left.Left == nil && root.Left.Right == nil {
     *res += root.Left.Val
 }

 if root.Left != nil {
     dfs(root.Left,res)
 }

 if root.Right != nil {
     dfs(root.Right,res)
 }

整体递归代码如下：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumOfLeftLeaves(root *TreeNode) int {
    if root == nil {
        return 0
    }
    res := 0
    dfs(root,&res)
    return res
}

func dfs(root *TreeNode,res *int) {
    if root == nil {
        return 
    }
    // 叶子节点没有左孩子，可以直接返回了
    if root.Left == nil && root.Right == nil {
        return 
    }

    // 要找的是父节点的左孩子，并且是叶子节点
    if root.Left != nil  && root.Left.Left == nil && root.Left.Right == nil {
        *res += root.Left.Val
    }

    if root.Left != nil {
        dfs(root.Left,res)
    }

    if root.Right != nil {
        dfs(root.Right,res)
    }
}

迭代法

本题迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了
判断条件都是一样的，代码如下：

func sumOfLeftLeaves(root *TreeNode) int {
        st := make([]*TreeNode, 0)
        if root == nil {
            return 0
        }
        st = append(st, root)
        result := 0

        for len(st) != 0 {
            node := st[len(st)-1]
            st = st[:len(st)-1]
            if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
                result += node.Left.Val
            }
            if node.Right != nil {
                st = append(st, node.Right)
            }
            if node.Left != nil {
                st = append(st, node.Left)
            } 
        }

        return result
}

总结

这道题目要求左叶子之和，其实是比较绕的，因为不能判断本节点是不是左叶子节点。

此时就要通过节点的父节点来判断其左孩子是不是左叶子了。

平时我们解二叉树的题目时，已经习惯了通过节点的左右孩子判断本节点的属性，而本题我们要通过节点的父节点判断本节点的属性。

希望通过这道题目，可以扩展大家对二叉树的解题思路。